Slīps sviediens
Nosacījumi
- Gaisa pretestību neievēro.
- Uz ķermeni lidojuma laikā darbojas tikai viens spēks – smaguma spēks (gravitācijas spēks).
- Brīvas krišanas paātrinājums \(g\) ir vienāds ar \(9,81\approx{10}\frac{m}{s^2}\) , vērsts tieši uz leju!
Kā modelē kustību (1. attēls).
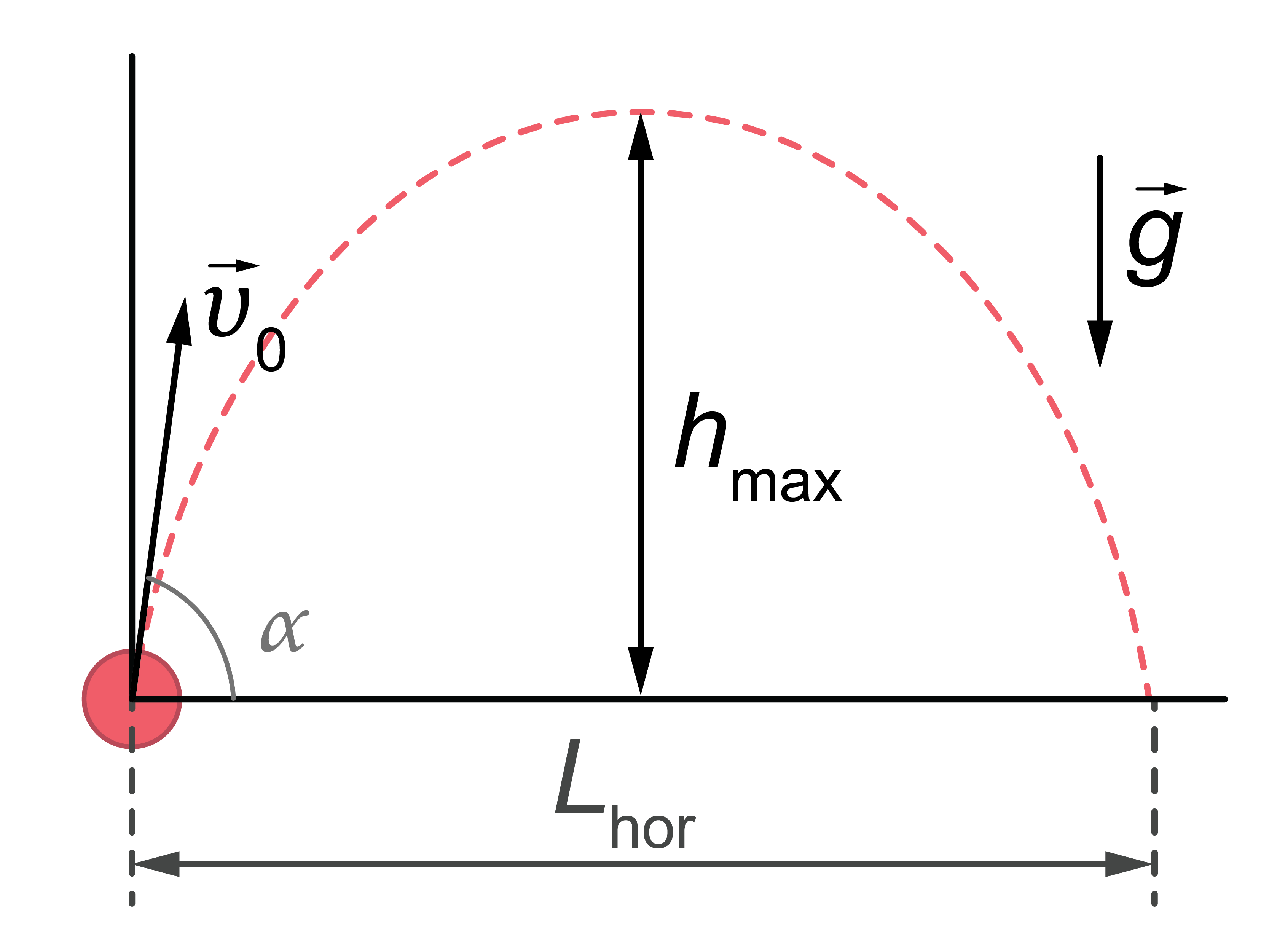
1.att.
- Lidojuma trajektorija – parabola.
- Reālo kustību sadala "divās kustības" mākslīgi.
- Kustība pa horizontāli – vienmērīga (nav "horizontālo'' spēku).
- Kustība pa vertikāli – brīvā krišana.
- Abas kustības "apvieno" laiks (cik ilgi ķermenis lido pa vertikāli, tik pat ilgi ķermenis lido pa horizontāli).
Apzīmējums: \(L_\mathrm{hor}\) – lidojuma tālums pa horizontāli, \(h_\mathrm{max}\) – maksimālais pacelšanās augstums.
Sākuma ātruma komponente pa horizontāli: \(v_\mathrm{0hor}=v_{0}cos\alpha\) (kustība vienmērīga); sākuma ātruma komponente pa vertikāli: \(v_\mathrm{0vert}=v_{0}sin\alpha\) (2. attēls).
Kustības ātruma komponente pa horizontāli nemainās laikā: \(v_\mathrm{hor}=v_{0}cos\alpha=const\) .
Kustības ātruma komponenti pa vertikāli nosaka šādi: \(v_\mathrm{vert}=|v_{0}sin\alpha{-gt}|\) .
Pilno kustības ātrumu var noteikt, izmantojot Pitagora teorēmu: \(v=\sqrt{v^2_\mathrm{hor}+v^2_\mathrm{vert}}\) (2. attēls).
Ātruma moduli \(v\) lidojuma laikā var noteikt, izmantojot mehāniskās enerģijas nezūdamības likumu.
Izsviešanas punktā ķermeņa pilnā mehāniskā enerģija ir kinētiskā enerģija \(E_\mathrm{kin}=\frac{mv_0^2}{2}\) , kur \(m\) – ķermeņa masa. Jebkurā citā trajektorijas punktā \(h\) augstumā pilnā enerģija sastāv no kinētiskās enerģijas \(E^*_\mathrm{kin}=\frac{mv^2}{2}\) un potenciālās enerģijas \(E^*_\mathrm{pot}=mgh\) .
Iegūst vienādojumu: \(\frac{mv_0^2}{2}=\frac{mv^2}{2}+mgh\) .
Ātruma leņķi pret horizontu laika momentā \(t\) var noteikt šādi: \(tg\beta=\frac{|v_\mathrm{vert}|}{v_\mathrm{hor}}=\frac{|v_0sin\alpha-gt|}{v_0{cos\alpha}}\) (2. attēls).
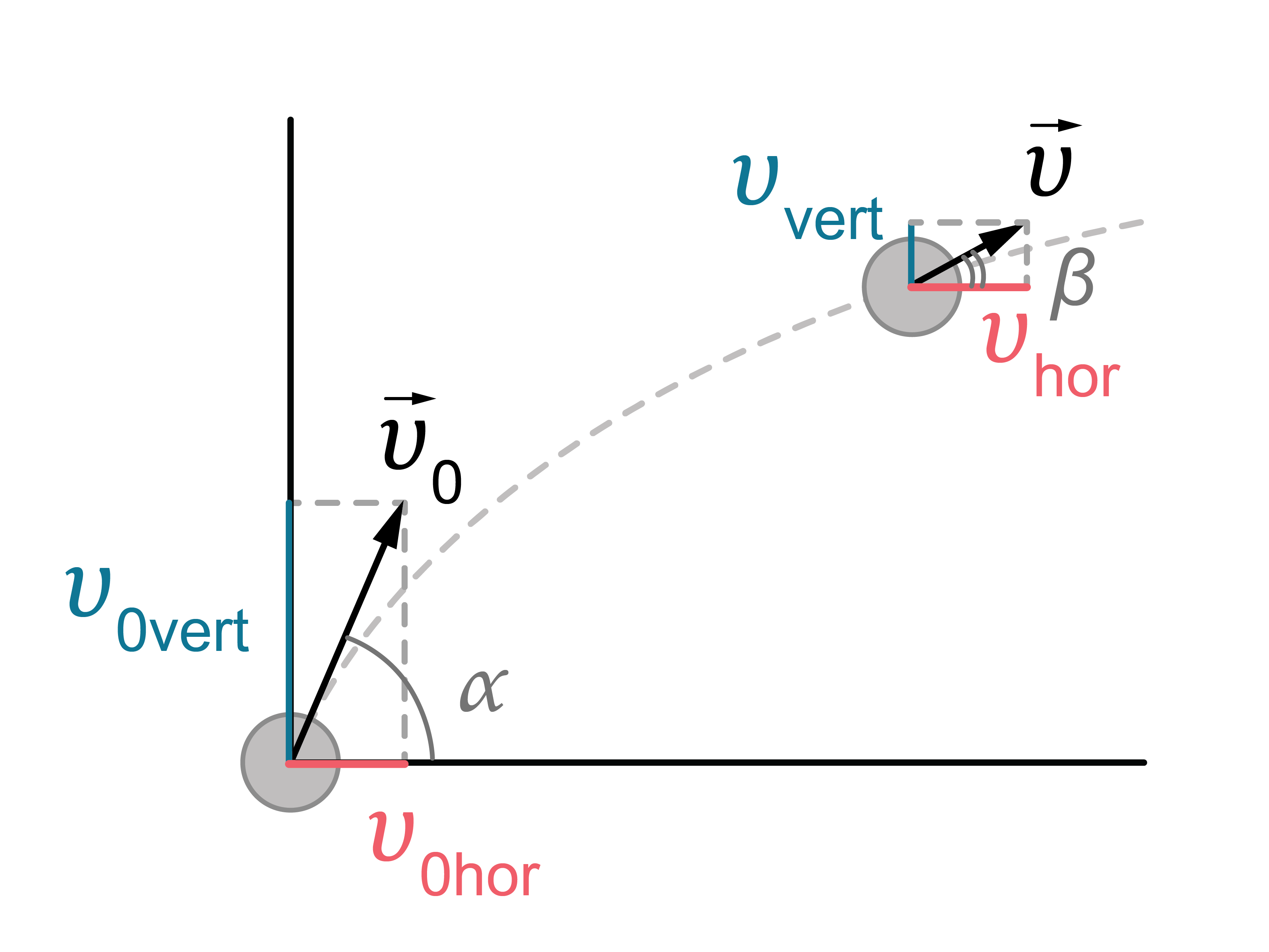
2.att.
Pacelšanās laiks
Izmantojam ātruma vertikālās komponentes formulu: \(v_\mathrm{vert}=|v_0{sin}\alpha-gt|\) .
Trajektorijas visaugstākajā punktā \(v_\mathrm{vert}=0\) . Var sastādīt vienādojumu: \(0=|v_0{sin}\alpha-gt|\) . Izsaka pacelšanās laiku: \(t=\frac{v_0{sin}\alpha}{g}\) .
Trajektorija ir simetriska, tātad kustības laiks "uz leju" ir tāds pats. Kopējais lidojuma laiks: \(t_\mathrm{kop}=\frac{2v_0sin\alpha}{g}\) .
Pacelšanās augstums. \(h_\mathrm{max}=\frac{v_\mathrm{0vert}^2}{2g}=\frac{(v_0sin\alpha)^2}{2g}\) .
Lidojuma tālums pa horizontāli. \(L_\mathrm{hor}=v_\mathrm{hor}t_\mathrm{kop}=v_0cos\alpha\frac{2v_0sin\alpha}{g}=\frac{v_0^2sin(2\alpha)}{g}\) .
Slīpo sviedienu var sadalīt arī citādi. No sākuma ķermenis lido uz augšu – pa vertikāli notiek vertikālais sviediens ar sākuma ātrumu \(v_\mathrm{0vert}=v_0sin\alpha\) , bet pa horizontāli notiek vienmērīga kustība ar ātrumu \(v_\mathrm{hor}=v_0cos\alpha\) . Pēc maksimālā augstuma sasniegšanas ķermenis lido uz leju – pa vertikāli notiek brīvā krišana, bet pa horizontāli notiek vienmērīga kustība ar ātrumu \(v_\mathrm{hor}=v_0cos\alpha\) .
Uzdevuma risināšanas piemērs
Ķermenis izviests leņķī pret horizontu no Zemes virsmas ar sākuma ātrumu \(50\frac{m}{s}\). Izsviešanas leņķis ir 30°. Noteikt:
- lidojuma laiku;
- pacelšanas augstumu;
- lidojuma tālumu pa horizontāli;
- ātrumu un pārvietojumu pēc \(2\) \(s\) kopš kustības sākuma.
Kopējais lidojuma laiks: \(t_\mathrm{kop}=\frac{2v_0sin\alpha}{g}=\frac{2\cdot{50}\cdot{sin30^\circ}}{10}=5\) \(s\).
Pacelšanās augstums: \(h_\mathrm{max}=\frac{(v_0sin\alpha)^2}{2g}=\frac{(50\cdot{sin30^\circ})^2}{2\cdot{10}}\approx{31,3}\) \(m\).
Lidojuma tālums pa horizontāli: \(L_\mathrm{hor}=\frac{v_0^2sin(2\alpha)}{g}=\frac{50^2sin60^\circ}{10}\approx{217}\) \(m\).
Ātruma modulis pēc \(2\) \(s\) kopš kustības sākuma: \(v=\sqrt{v^2_\mathrm{hor}+v^2_\mathrm{vert}}=\sqrt{(v_0cos\alpha)^2+(v_0sin\alpha-gt)^2}=\sqrt{(50\cdot{cos30^\circ})^2+(50\cdot{sin30^\circ}-10\cdot{2})^2}\approx{43,6}\) \(\frac{m}{s}\).
Ātruma virziens pēc \(2\) \(s\) kopš kustības sākuma: \(tg\beta=\frac{|v_0sin\alpha-gt|}{v_0cos\alpha}=\frac{|50\cdot{sin30^\circ}-10\cdot{2}|}{50\cdot{cos30^\circ}}\approx{0,16}\). Leņķis pret horizontu aptuveni vienāds 9,1°.
Pārvietojumu \(s\) pēc \(2\) \(s\) kopš kustības sākuma var noteikt pēc Pitagora teorēmas: \(s=\sqrt{L^2+h^2}\), kur \(L=v_0cos\alpha{t}\) – pārvietojums pa horizontāli, \(h=v_0sin\alpha{t}-\frac{gt^2}{2}\) – pārvietojums pa vertikāli.
\(L=50\cdot{cos30^\circ}\cdot{2}\approx{87}\) \(m\), \(h=50\cdot{sin30^\circ}\cdot{2}-\frac{10\cdot{2^2}}{2}=30\) \(m\), \(s=\sqrt{87^2+30^2}\approx{92}\) \(m\).