Brīvā krišana
Nosacījumi
- Gaisa pretestību neievēro.
- Uz ķermeni lidojuma laikā darbojas tikai viens spēks – smaguma spēks (gravitācijas spēks).
- Brīvas krišanas paātrinājums \(g\) ir vienāds ar \(9,81\approx{10}\frac{m}{s^2}\) , vērsts tieši uz leju.
Brīvā krišana ir vienmērīgi mainīgas (paātrinātas) kustības īpašs gadījums (speciālgadījums). Kustība notiek no miera stāvokļa – ķermeņa sākuma ātrums \(v_0\) ir vienāds ar nulli (1. attēls).
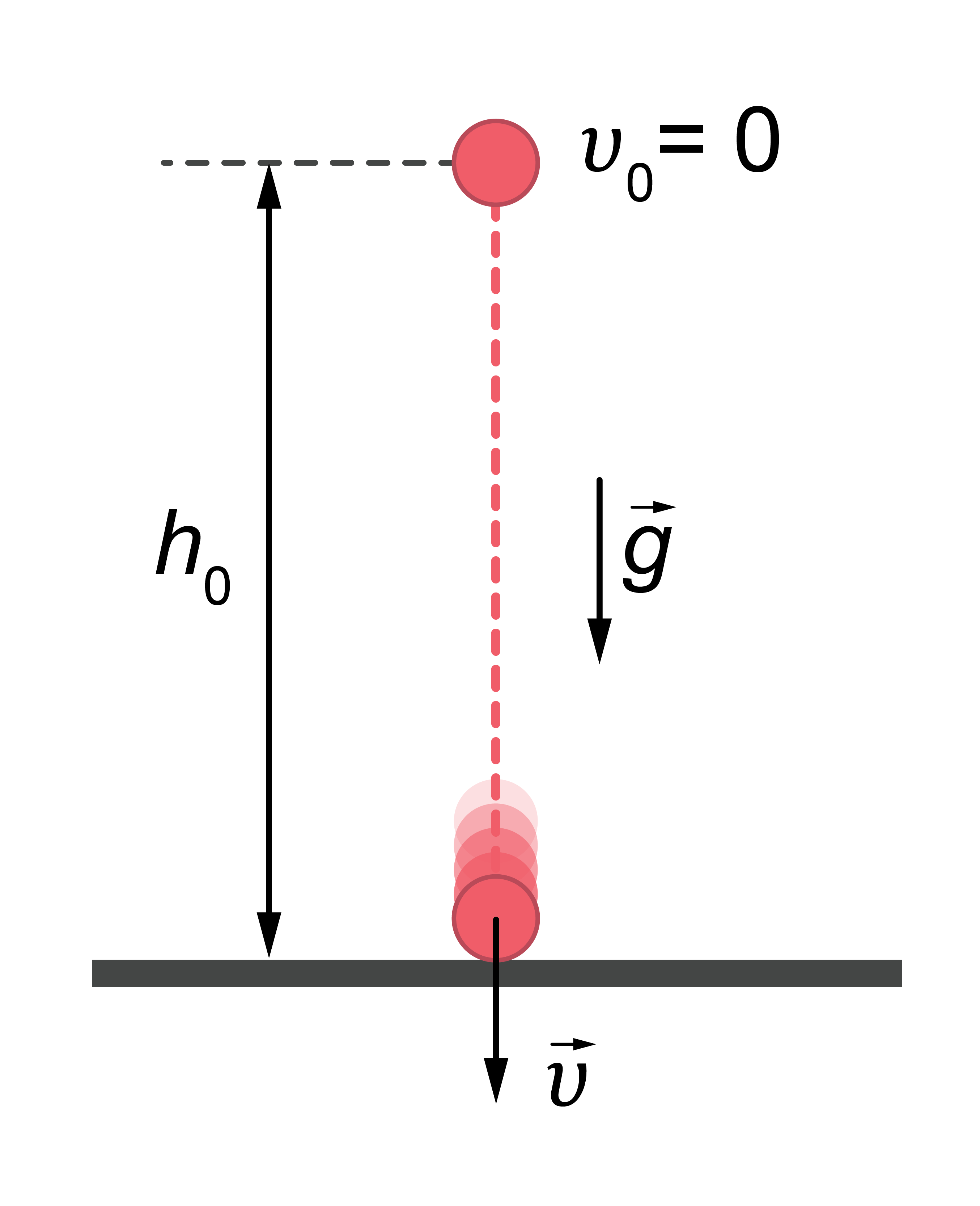
1.att.
Izmantosim vienmērīgi paātrinātas kustības formulas – ātruma formulu: \(v=v_0+at\) un pārvietojuma (ceļa) formulu \(s=v_0t+\frac{at^2}{2}\) . Ņemsim vērā, \(v_0=0\), \(a=g\) un \(s=h_0\) . Iegūstam: \(v=gt\) un \(h_0=\frac{gt^2}{2}\) , kur \(v\) – ķermeņa beigu ātrums (pie Zemes virsmas), \(t\) – kustības laiks līdz Zemes virsmai.
Ja no formulas \(h_0=\frac{gt^2}{2}\) izsaka krišanas laiku \(t=\sqrt{\frac{2h_0}{g}}\) un ievieto formulā \(v=gt\) , tad var aprēķināt beigu ātrumu atkarībā no krišanas augstuma: \(v=g\sqrt{\frac{2h_0}{g}}=\sqrt{2gh_0}\) .
Kustībai atbilst ātruma grafiks (2. attēls), kur ātrums pieaug lineāri. Laukums zem grafika līknes atbilst veiktajam ceļam. Mūsu gadījumā – veiktais ceļš ir krišanas augstums \(h_0\) . No attēla ir redzams: \(h_0=\frac{vt}{2}\) .
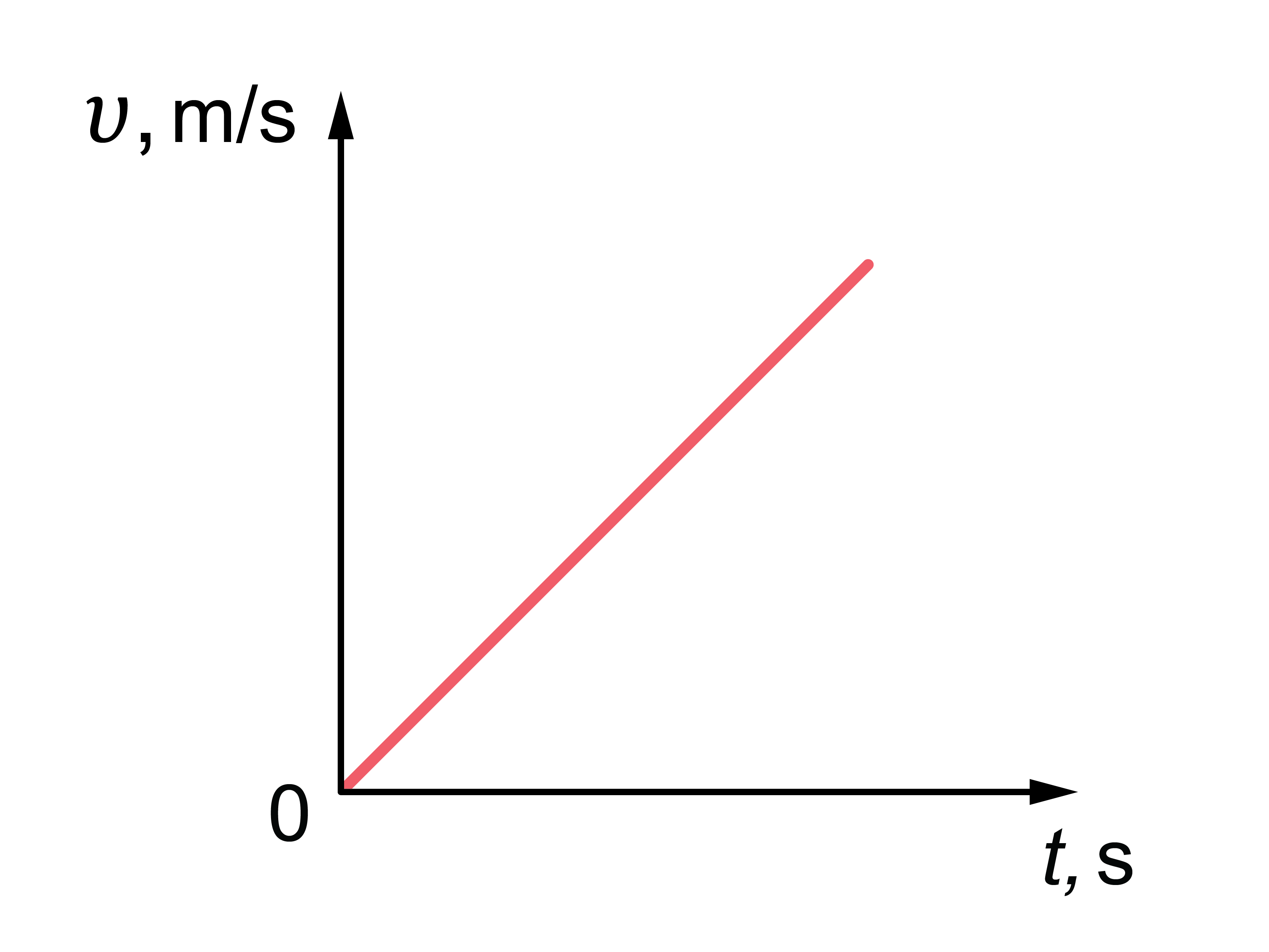
2.att.
Tātad beigu ātrumu var noteikt šādi: \(v=\frac{2h_0}{t}\) , kur \(t\) – krišanas laiks (3. attēls).
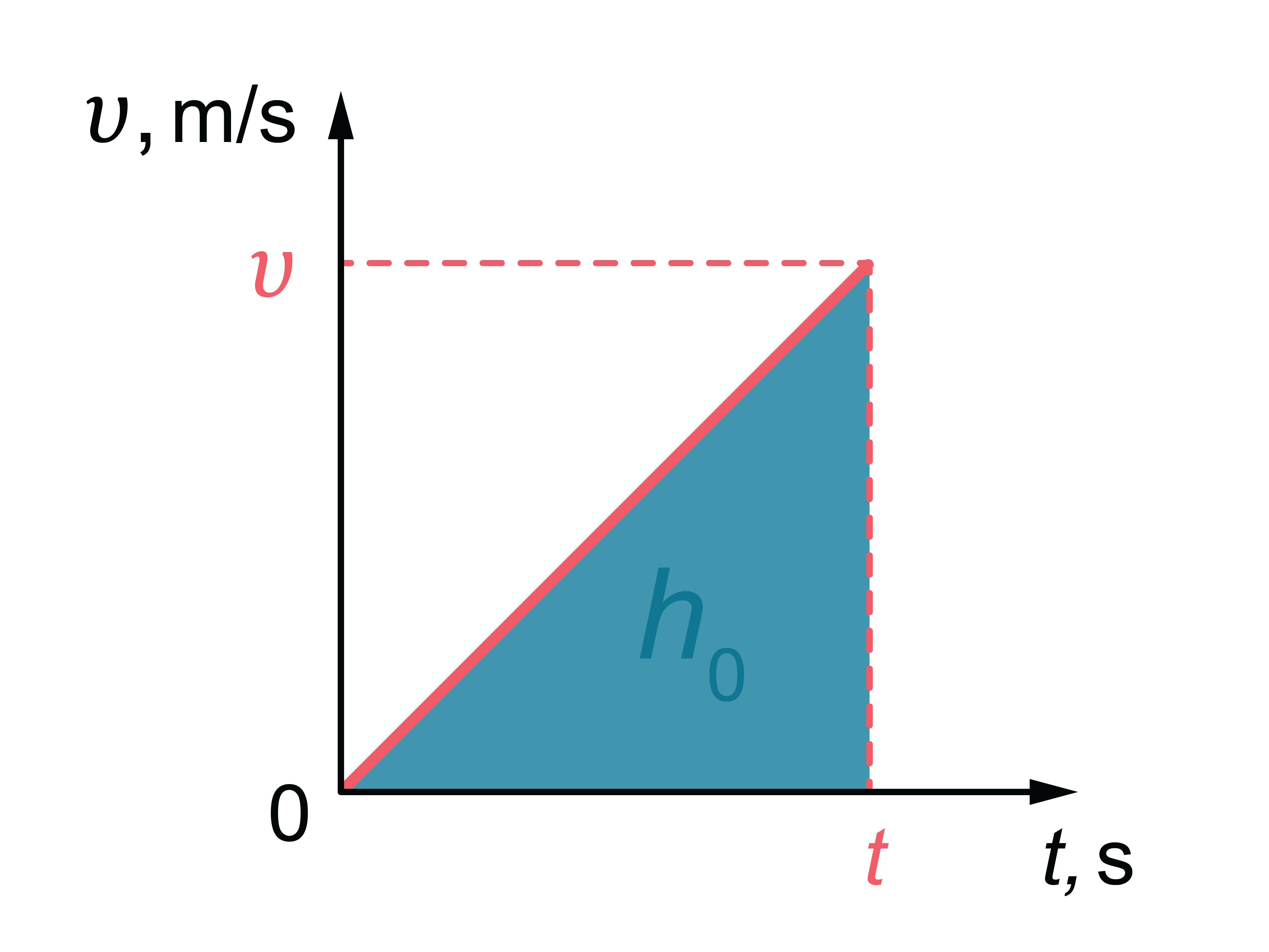
3.att.
Ķermeņa beigu ātrumu var noteikt arī izmantojot mehāniskās enerģijas nezūdamības likumu. Trajektorijas sākuma punktā ķermenim piemīt tikai potenciāla enerģija \(E_\mathrm{pot}=mgh_0\) , bet trajektorijas beigu punktā – tikai kinētiskā enerģija \(E_\mathrm{kin}=\frac{mv^2}{2}\) . Pielīdzinot izteiksmes \(mgh_0=\frac{mv^2}{2}\) izsaka ķermeņa beigu ātrumu \(v=\sqrt{2gh_0}\) .
Piezīme. Ja formulās \(v=gt\) un \(h_0=\frac{gt^2}{2}\) izmanto laiku \(t\), kas ir mazāks, nekā krišanas laiks, iegūst ātrumu un veikto ceļu konkrētajā laika momentā.
Uzdevuma risināšanas piemērs
Ābols brīvi krīt no Zaķu salas televīzijas torņa skatu laukuma. Skatu laukuma augstums \(h_0=100\) \(m\). Noteiksim krišanas laiku un ķermeņa beigu ātrumu pie Zemes virsmas.
Ābola krišanas laiks: \(t=\sqrt{\frac{2h_0}{g}}=\sqrt{\frac{2\cdot{100}}{10}}\approx4,5\)\(s\) .
Ābola beigu ātrums: \(v=\sqrt{2\cdot{10}\cdot{100}}\approx45\frac{m}{s}\) .
Vertikāls sviediens
Nosacījumi
- Gaisa pretestību neievēro.
- Uz ķermeni lidojuma laikā darbojas tikai viens spēks – smaguma spēks (gravitācijas spēks).
- Brīvas krišanas paātrinājums \(g\) ir vienāds ar \(9,81\approx{10}\frac{m}{s^2}\) , vērsts tieši uz leju.
Vertikālais sviediens ir vienmērīgi mainīgas (palēninātas) kustības īpašs gadījums (speciālgadījums) (1. attēls).
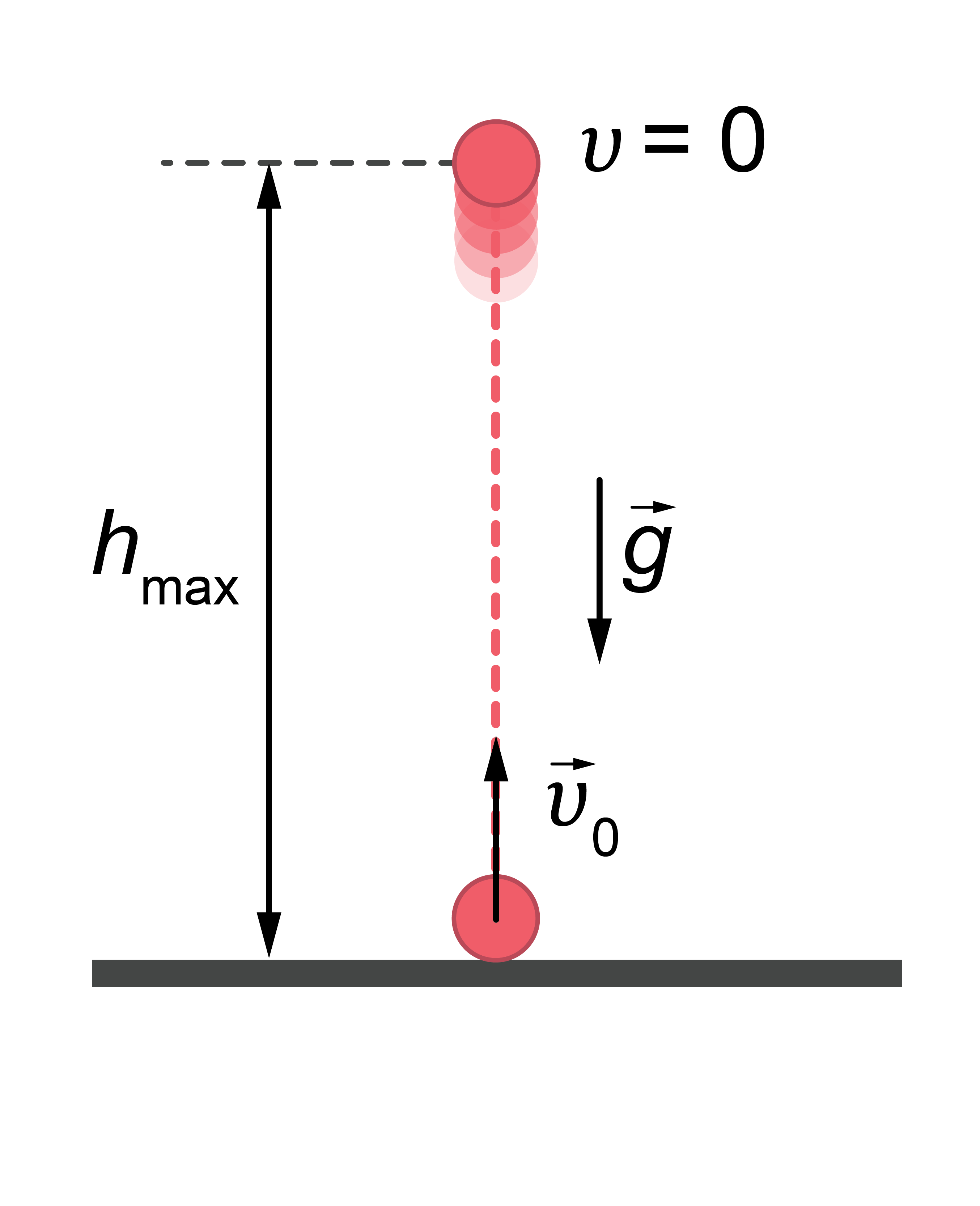
1.att.
Izmanto vienmērīgi palēninātas kustības formulas. Ātruma formulu \(v=v_0-at\) un pārvietojuma (ceļa) formulu \(s=v_0t-\frac{at^2}{2}\) .
Ņem vērā, ka \(v=0\) (beigu ātrums maksimālajā pacelšanās augstumā \(h_\mathrm{max}\)), \(a=g\) un \(s=h_\mathrm{max}\) . Iegūst: \(0=v_0-gt\) un \(h_\mathrm{max}=v_0t-\frac{gt^2}{2}\) , kur \(t\) – ķermeņa pacelšanās laiks.
No formulas \(0=v_0-gt\) izsaka pacelšanās laiku: \(t=\frac{v_0}{g}\) .
Izmantojot divas formulas \(h_\mathrm{max}=v_0t-\frac{gt^2}{2}\) un \(t=\frac{v_0}{g}\) , iegūst maksimālā augstuma izteiksmi:
\(h_\mathrm{max}=v_0\frac{v_0}{g}-\frac{g(\frac{v_0}{g})^2}{2}=\frac{v_0^2}{g}-\frac{v_0^2}{2g}=\frac{v_0^2}{2g}\) .
Maksimālo augstumu hmax var noteikt arī izmantojot ātruma grafiku (2. attēls).
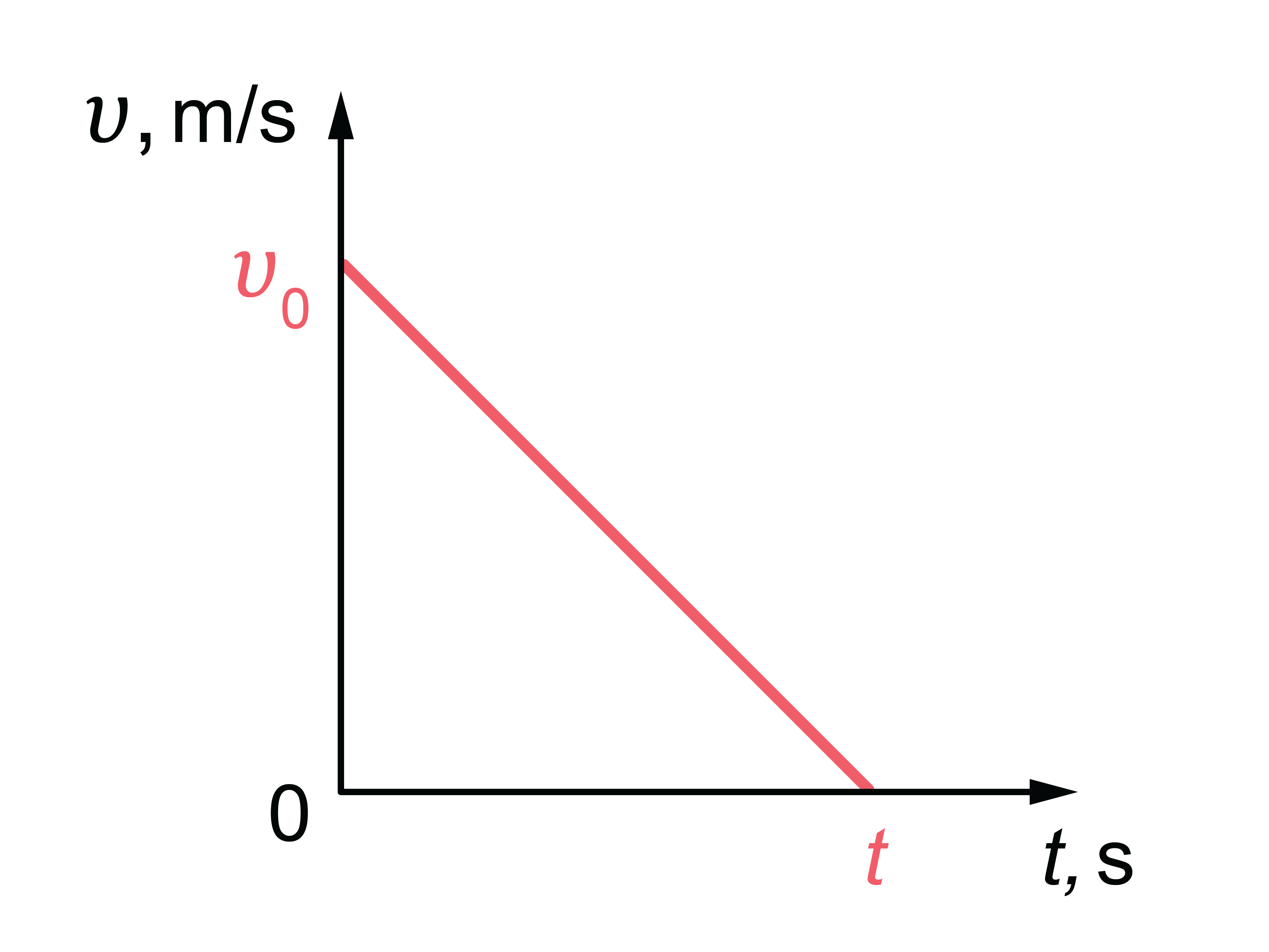
2.att.
Ķermeņa kustības ātrums samazinās lineāri. Laukums zem grafika līknes atbilst veiktajam ceļam (3. attēls). Mūsu gadījumā – veiktais ceļš ir maksimālais augstums \(h_\mathrm{max}\) . No attēla ir redzams: \(h_\mathrm{max}=\frac{v_0t}{2}\) . Izteiksme \(\frac{v_0}{2}\) ir kustības vidējais ātrums (3. attēls).
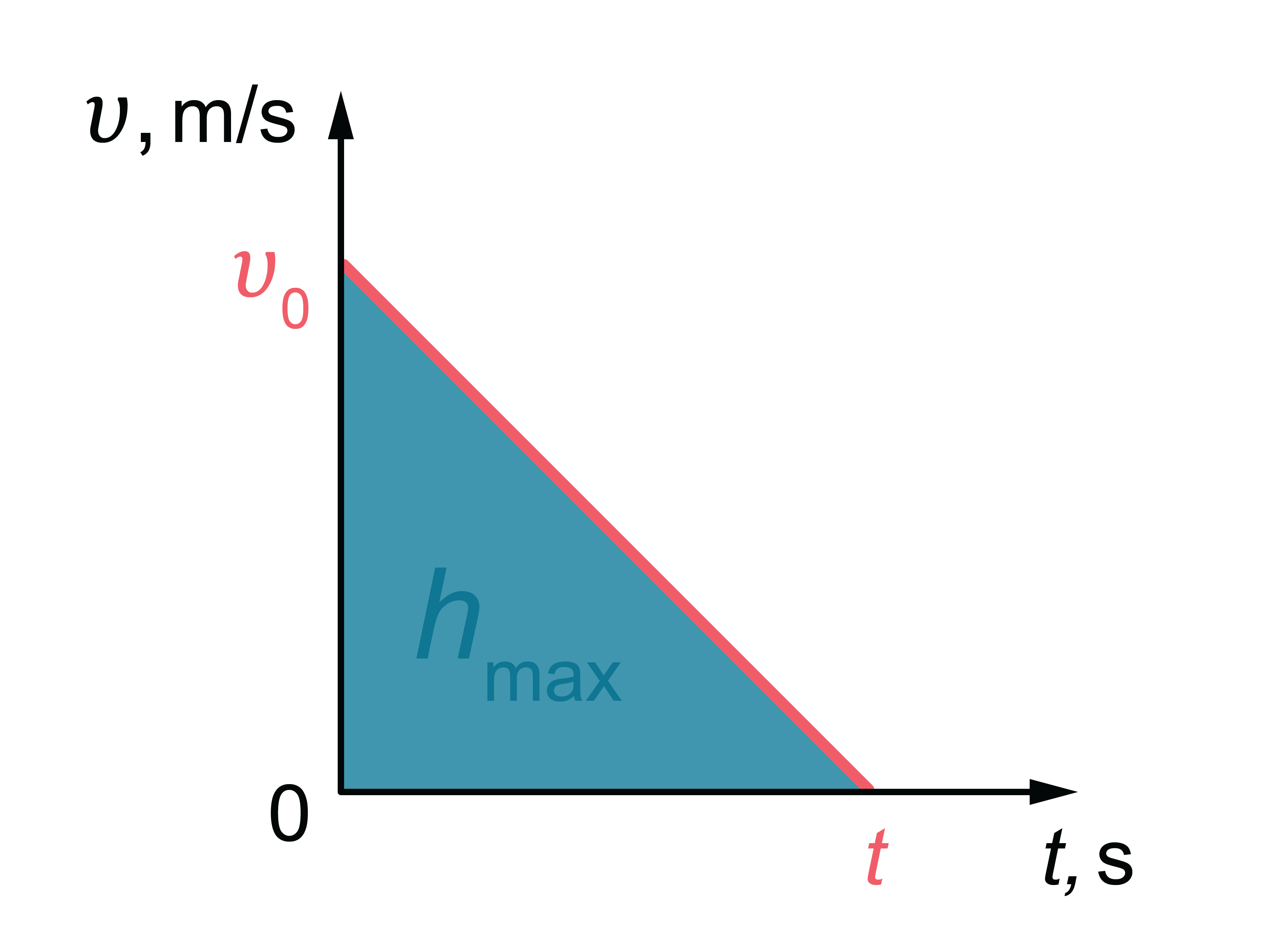
3.att.
Maksimālo augstumu \(h_\mathrm{max}\) var noteikt arī izmantojot mehāniskās enerģijas nezūdamības likumu.
Trajektorijas sākuma punktā ķermenim piemīt tikai kinētiskā enerģija \(E_\mathrm{kin}=\frac{mv_0^2}{2}\) , bet trajektorijas beigu punktā – tikai potenciāla enerģija \(E_\mathrm{pot}=mgh_\mathrm{max}\) . Pielīdzina izteiksmes \(mgh_\mathrm{max}=\frac{mv_0^2}{2}\) un nosaka maksimālo augstumu \(h_\mathrm{max}=\frac{v_0^2}{2g}\) .
Piezīme. Ja formulās \(v=v_0-gt\) un \(h=v_0t-\frac{gt^2}{2}\) izmanto laiku \(t\), kas ir mazāks, nekā pacelšanās laiks, iegūst ķermeņa ātrumu un pacelšanās augstumu konkrētajā laika momentā.
Uzdevuma risināšanas piemērs
Sportists no vietas veica lēcienu \(1\) \(m\) augstumā. Noteikt sportista sākuma ātrumu un lēciena laiku.
No formulas \(h_\mathrm{max}=\frac{v_0^2}{2g}\) nosaka sākuma ātrumu \(v_0=\sqrt{2gh}_\mathrm{max}\) un ieliec skaitliskās vērtības: \(v_0=\sqrt{2\cdot{10}\cdot{1}}\approx{4,5}\frac{m}{s}\) .
No formulas \(0=v_0-gt\) nosaka lēciena laiku \(t=\frac{v_0}{g}\) ieliec skaitliskās vērtības: \(t=\frac{4,5}{10}\approx0,45\) \(s\).
Piezīmes brīvajai krišanai un vertikālajam sviedienam
1. Var izmantot brīvas krišanas paātrinājuma fizikālo jēgu – katru sekundi ātrums mainās par \(10 \) \(m/s\).
Piemērs:
- ja ķermenis izsviests vertikāli uz augšu ar sākuma ātrumu \(v_0=60\frac{m}{s}\), tad pacelšanās laiks ir vienāds ar \(6\) \(s\) (katru sekundi ātrums samazinās par \(10\frac{m}{s}\));
- ja ķermenis brīvi krīt \(6\) \(s\), tad beigu ātrums būs \(60\frac{m}{s}\) (katru sekundi ātrums palielinās par \(10\frac{m}{s}\)).
2. Brīvo krišanu un vertikālo sviedienu var aplūkot "spoguļveidā". Ja ķermenis brīvi krīt no augstuma \(h_0\) un ķermeņa beigu ātrums ir vienāds \(v\), tad vertikālajā sviedienā ar sākuma ātrumu \(v\) maksimālais augstums būs \(h_0\). Krišanas laiks un pacelšanās laiks būs vienādi.
Piemērs:
- ja ķermenis brīvi krīt no augstuma \(180\) \(m\), tad beigu ātrums būs vienāds ar \(60\frac{m}{s}\);
- ja vertikālajā sviedienā ķermeņa sākuma ātrums ir \(60\frac{m}{s}\), tad maksimālais pacelšanās augstums būs \(180\) \(m\).
Horizontāls sviediens
Nosacījumi
- Gaisa pretestību neievēro.
- Uz ķermeni lidojuma laikā darbojas tikai viens spēks – smaguma spēks (gravitācijas spēks).
- Brīvas krišanas paātrinājums \(g\) ir vienāds ar \(9,81\approx{10}\frac{m}{s^2}\) , vērsts tieši uz leju.
Kā modelē kustību (1. attēls).
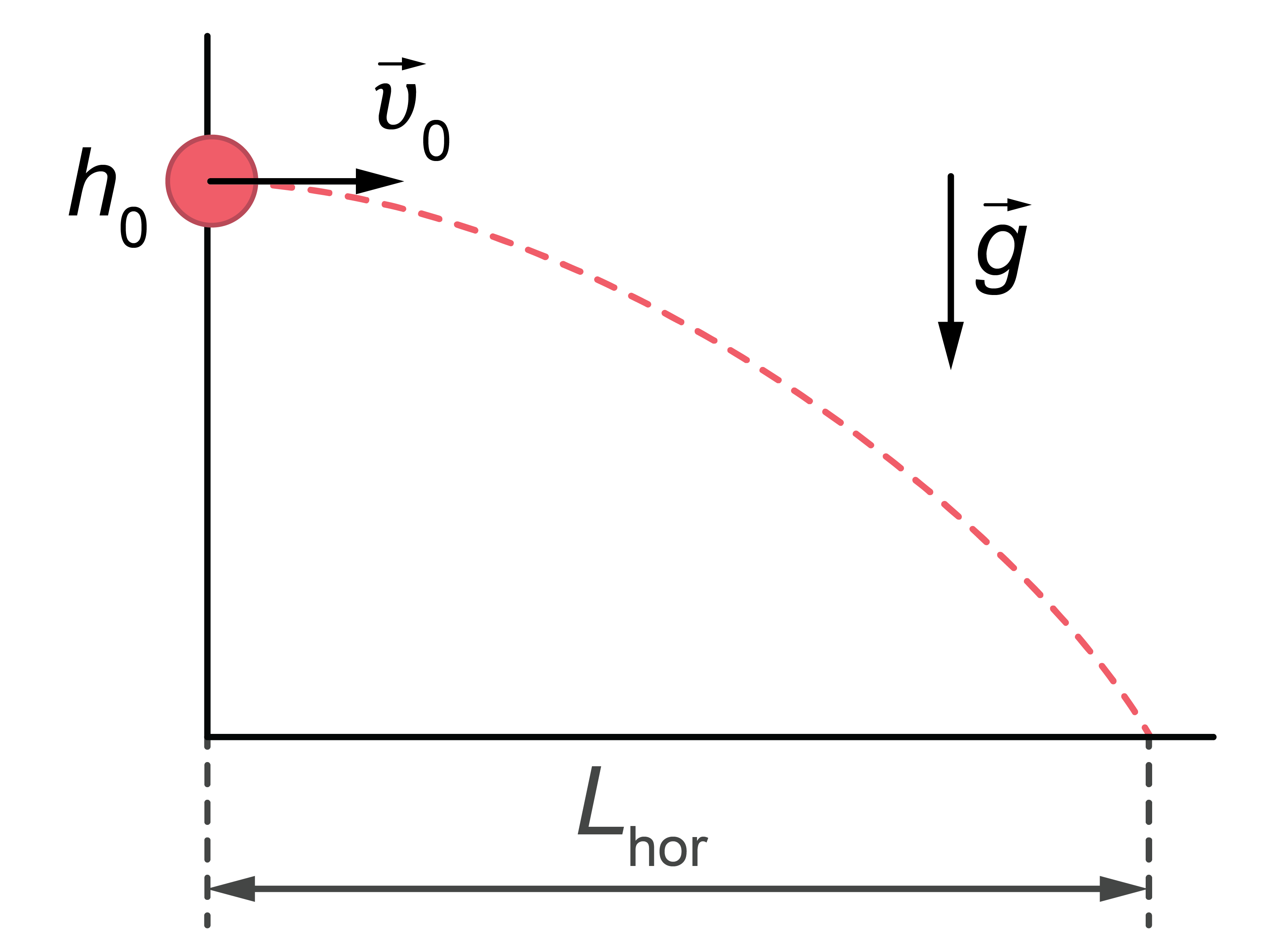
1.att.
- Lidojuma trajektorija – parabolas zars.
- Reālo kustību mākslīgi sadala "divās kustībās".
- Kustība pa horizontāli – vienmērīga (nav "horizontālo'' spēku).
- Kustība pa vertikāli – brīvā krišana.
- Abas kustības "apvieno" laiks (cik ilgi ķermenis lido pa vertikāli, tikpat ilgi ķermenis lido pa horizontāli).
Apzīmējums: \(L_\mathrm{hor}\) – lidojuma tālums pa horizontāli.
Vertikālā kustība
Izmanto formulu \(h_0=\frac{gt^2}{2}\) . Iegūst lidojuma laiku: \(t=\sqrt{\frac{2h_0}{g}}\) . Lidojuma laiks (ilgums) nav atkarīgs no sākuma ātruma!
Izmanto formulu \(v=gt\) , kur ķermeņa beigu ātruma vertikālā komponente. Tātad beigu ātruma vertikālā komponente: \(v=g\sqrt{\frac{2h_0}{g}}\) .
Horizontālā kustība
Kustības ātrums horizontālā virzienā ir nemainīgs. Izmanto formulu \(L_\mathrm{hor}=v_0t\) . Ievieto lidojuma laiku \(t=\sqrt{\frac{2h_0}{g}}\) un iegūst \(L_\mathrm{hor}=v_0\sqrt{\frac{2h_0}{g}}\) .
Par beigu ātrumu
Sākuma ātrums vērsts horizontāli un lidojuma laikā ātruma horizontālā komponente nemainās. Pa vertikāli notiek brīvā krišana: \(v=v_0+gt\) . Bet sākuma ātrums pa vertikāli ir \(0\), tādēļ \(v=gt\) .
Beigu ātrumu \(v_\mathrm{b}\) nosaka, izmantojot Pitagora teorēmu (2. attēls): \(v_\mathrm{b}=\sqrt{v_0^2+(gt)^2}\) .
Ja lidojuma laika \(t\) vietā izteiksmē ieliek \(\sqrt{\frac{2h_0}{g}}\) , tad var iegūt beigu ātrumam b citu formulu: \(v_\mathrm{b}=\sqrt{v_0^2+(g\sqrt{\frac{2h_0}{g}}^2)}=\sqrt{v_0^2+2gh_0}\) .
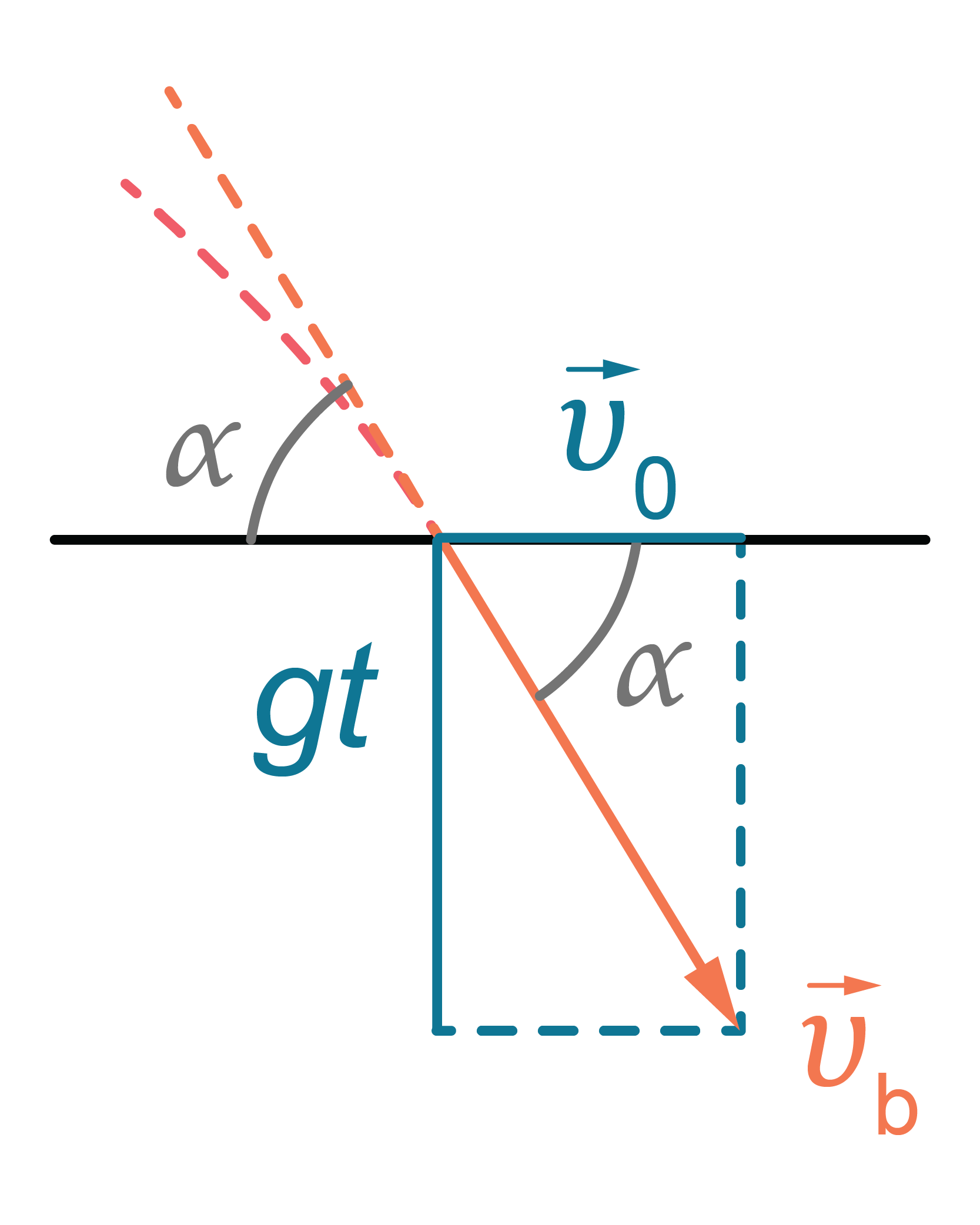
2.att.
Beigu ātruma \(v_\mathrm{b}\) moduli var noteikt arī, izmantojot mehāniskās enerģijas nezūdamības likumu. Trajektorijas sākuma punktā ķermenim piemīt pilnā mehāniskā enerģija \(E_\mathrm{pilnā}=\frac{mv_0^2}{2}+mgh_0\) . Bet trajektorijas beigu punktā – pilnā mehāniskā enerģija ir ķermeņa kinētiskā enerģija \(E_\mathrm{pilnā}=\frac{mv_b^2}{2}\) . Pielīdzina izteiksmes \(\frac{mv_0^2}{2}+mgh_0=\frac{mv_\mathrm{b}^2}{2}\) nosaka ķermeņa beigu ātrumu \(v_\mathrm{b}=\sqrt{v_0^2+2gh_0}\) .
Beigu ātruma virzienu nosaka, izmantojot trigonometrijas formulu (2. attēls): \(tg\alpha=\frac{gt}{v_0}\) .
Piezīme. Ja formulās: \(h=\frac{gt^2}{2}\) , \(l=v_0t\) , \(v_\mathrm{b}=\sqrt{v_0^2+(gt)^2}\) , \(tg\alpha=\frac{gt}{v_0}\) izmanto laiku \(t\), kas ir mazāks, nekā lidojuma laiks, iegūst pārvietojumus pa vertikāli un pa horizontāli, kā arī ātrumu konkrētajā laika momentā.
Uzdevuma risināšanas piemērs
Sportists no baseina torņa, kura augstums \(h_0=10\) \(m\) veic lēcienu horizontālā virzienā ar sākuma ātrumu \(v_0=4\frac{m}{s}\) . Noteikt sportista lidojuma laiku, lidojuma tālumu pa horizontāli un beigu ātrumu pie ūdens virsmas.
No formulas \(h_0=\frac{gt^2}{2}\) nosaka lidojuma laiku \(t=\sqrt{\frac{2h_0}{g}}\) un ievieto skaitliskās vērtības: \(t=\sqrt{\frac{2\cdot{10}}{10}}\approx{}1,4\) \(s\) .
No formulas \(L_\mathrm{hor}=v_0t\) iegūst lidojuma tālumu pa horizontāli: \(L_\mathrm{hor}=4\cdot{1,4}=5,6\) \(m\) .
Beigu ātrumu \(v_\mathrm{b}\) var noteikt šādi: \(v_\mathrm{b}=\sqrt{v_0^2+2gh_0}=\sqrt{4^2+2\cdot{10}\cdot{10}}\approx14,7\frac{m}{s}\) .
Beigu ātruma leņķi pret ūdens virsmu nosaka, izmantojot trigonometrijas formulu: \(tg\alpha=\frac{gt}{v_0}=\frac{10\cdot{1,4}}{4}\approx{3,5}\). Leņķis \(\alpha\approx{74}\)°.