Mērīt var divos veidos:
1) tieši,
2) netieši.
Tiešā mērīšana nozīmē, ka fizikālo lielumu nolasa tieši no mērinstrumenta, bet netiešajā mērīšanā fizikālo lielumu iegūst, izmantojot kādu formulu, kurā ietilpstošie lielumi tiek izmērīti, izmantojot tiešo mērīšanu. Ir daži fizikālie lielumi, kurus var noteikt, izmantojot gan tiešo, gan netiešo mērīšanu. Piemēram, ja mēs vēlamies noteikt, cik augsts ir kāds pie mājas augošs koks, tad varam ņemt mērlenti un sākt mērīt tā augstumu h1, bet tas ir neērti un var izrādīties arī bīstami (1. att. a). Pastāv iespēja augstumu izmērīt arī netieši, izmantojot koka ēnu un kādu priekšmetu, piemēram, cilvēka augumu, kam ir zināms vai viegli izmērāms augstums h2. Cilvēkam ir jānostājas vertikāli pret zemi uz jāizmēra tā veidotās ēnas garums l2. Ja cilvēka augumu h2 izdala ar tā ēnas garumu l2 un to visu pareizina ar koka ēnas garumu l1, tad iegūst koka augstumu h1 (1. att. b).
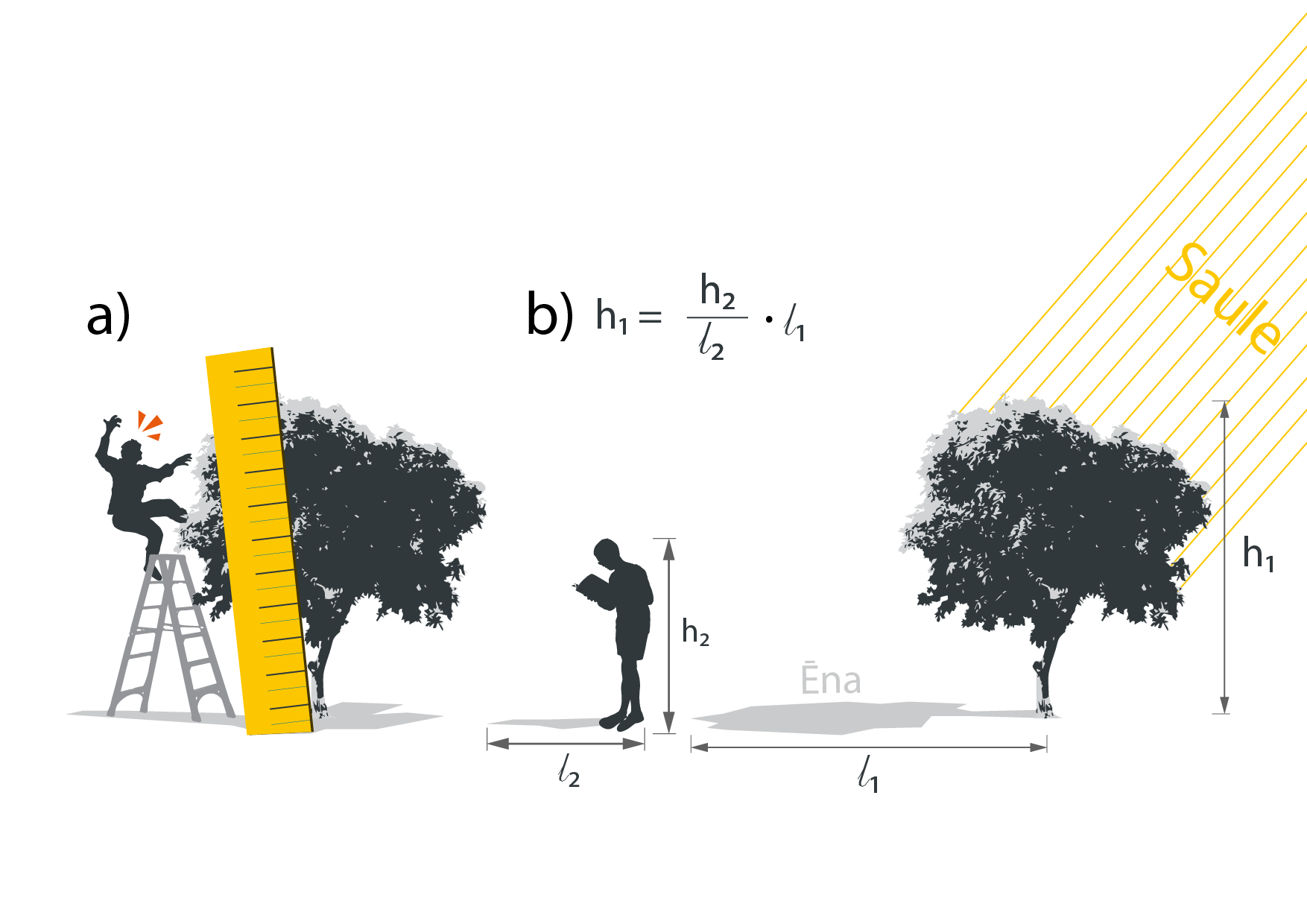
1.att. Tiešā un netiešā mērīšana
Daļu no fizikālajiem lielumiem raksturo tikai tā vērtība – skaitlis. Piemēram, mums ir trauks, kurā atrodas ūdens ar tilpumu V1 = 0,4 l. Veicot matemātiskas darbības ar šo fizikālo lielumu, nozīme ir tikai skaitlim, piemēram, ja mēs salejam kopā 0,4 l ūdens ar 0,3 l ūdens, iegūstam 0,7 l ūdens (2. att. a). Šādus fizikālos lielumus sauc par skalāriem. Ja papildus skaitliskajai vērtībai fizikālo lielumu raksturo arī virziens, tad to sauc par vektoriālu lielumu. Piemēram, ja virves vilcēju komanda savā virzienā pieliek spēku F1 = 10 000 N, bet pretējā komanda velk pretī ar spēku F2 = 8000 N, tad kopējo spēku F iegūst, ja no F1 atņem F2 (2. att. b). Šajā gadījumā jālieto vektoru ģeometriskā saskaitīšana.
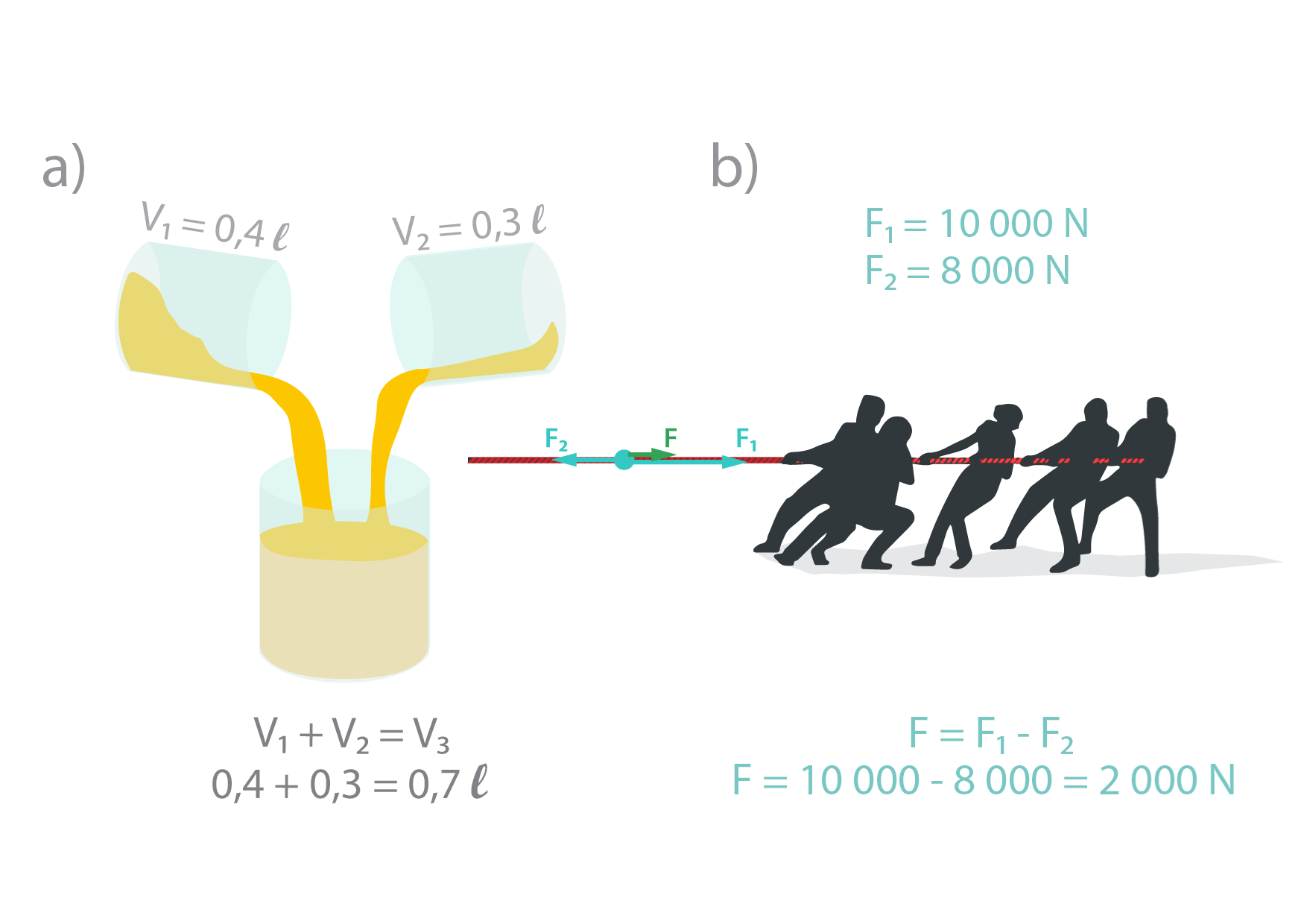
2.att. Skalārs (a) un vektoriāls (b) lielums
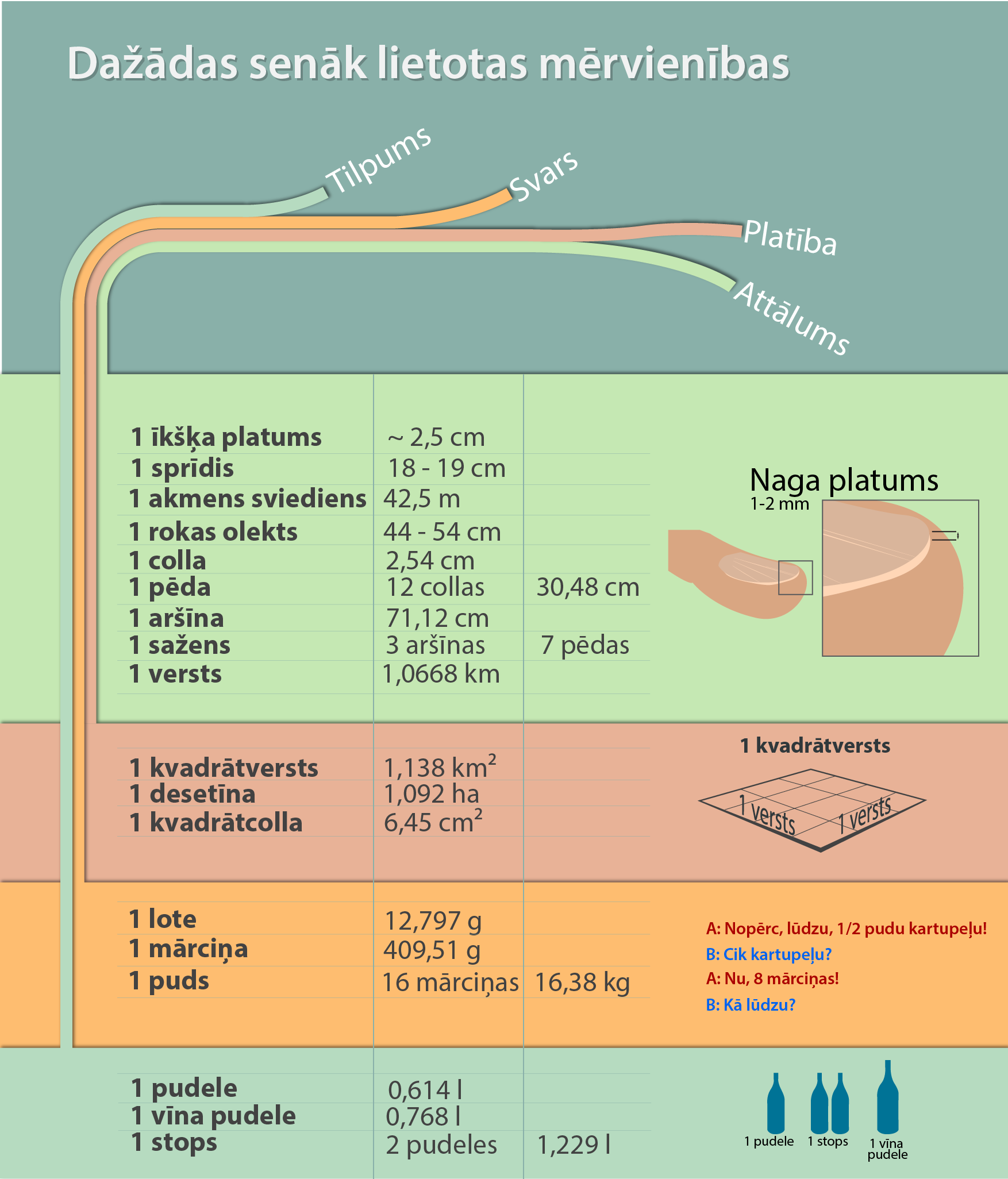
Lai arī mēs zinām, kāds fizikālais lielums tiek mērīts, ir daudz un dažādu mērvienību, kurās var šo lielumu izteikt. Piemēram, garumu un attālumu var mērīt centimetros, metros, collās, jūdzēs, jardos, un Latvijā senos laikos tika lietota arī tāda mērvienība kā vērša māviens (3. att.). Šīs atšķirības radīja lielas neērtības, tādēļ 1960. gadā tika pieņemta Starptautiskā mērvienību sistēma (SI), kurā kopumā ir septiņas pamatmērvienības. Iedomājieties, kā būtu, ja mēs savu garumu mērītu papagaiļos?

3.att. Vēsturiskais vērša māviens
Dažkārt, lai rezultāti būtu vieglāk uztverami, nelieto SI sistēmas pamatvienības, bet citas pieņemtas mērvienības un SI sistēmas mērvienību daudzkārtņus un daļas (4. att.)
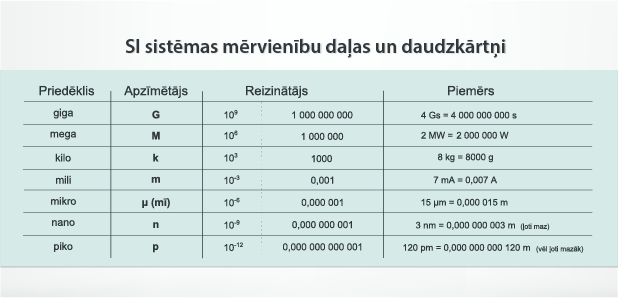
4.att. SI mērvienību daļas vai to daudzkārtņi
Apskatīsim viena pētījuma piemēru un to, kā tajā atklājas apskatītie mērāmie lielumi. Piemēram, dzīvojot un pārvietojoties pa lauku teritorijām, nākas saskarties ar dažādiem teritorijas segumiem un šķēršļiem mūsu ceļā, piemēram, pļavām, vagām, meža ceļiem, grāvjiem, lāci, kokiem. Atkarībā no mūsu pārvietošanās veida katrs no šiem elementiem kustību ietekmē citādāk, jo sastapšanās ar lāci, ejot kājām vai braucot mašīnā, ir nedaudz citādāka. Pieņemsim, ka mūsu rīcībā ir velosipēds, automašīna – visurgājējs, kā arī varam iet kājām. Pētījumā tiks izmantoti visi šie pārvietošanās līdzekļi, lai noskaidrotu, kurš izvēlētajā maršrutā (1. att.) ir visātrākais.
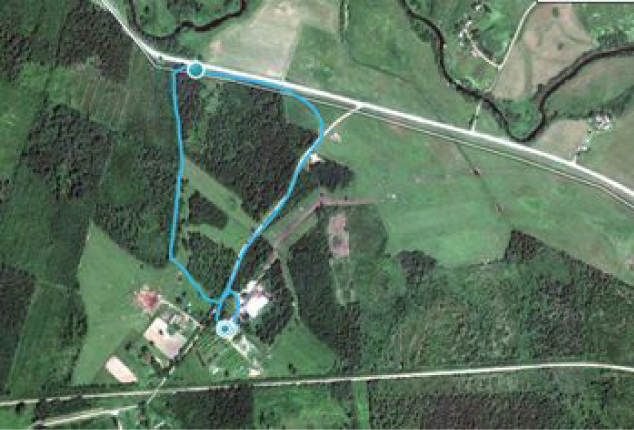
1.att. Izvēlētais maršruts
Mērot paveikto attālumu un ceļā pavadīto laiku, pētījumā tika iegūti 2. attēlā redzamie rezultāti. Redzams, ka šeit nav lietota SI sistēma, bet citas pieņemtas mērvienības un SI sistēmas mērvienību daudzkārtņi, lai rezultāti būtu vieglāk uztverami.

2.att. Pētījumā iegūtie dati
Gan attālums, gan laiks šajā gadījumā tika mērīti tieši, jo tika nolasīti no mērierīces – ar GPS aprīkota viedtālruņa (3. att.).

3.att. Pētījumā izmantotais viedtālrunis ar GPS
Tomēr, ja pētījumā būtu, piemēram, jānosaka kustības vidējais ātrums, tad tā jau būtu netiešā mērīšana, jo kustības attālums un laiks tiktu izmērīts tieši, bet ātrumu aprēķinātu, izmantojot formulu v = l : t, kā tas ir izdarīts kustībai bez transporta līdzekļa 4. attēlā.
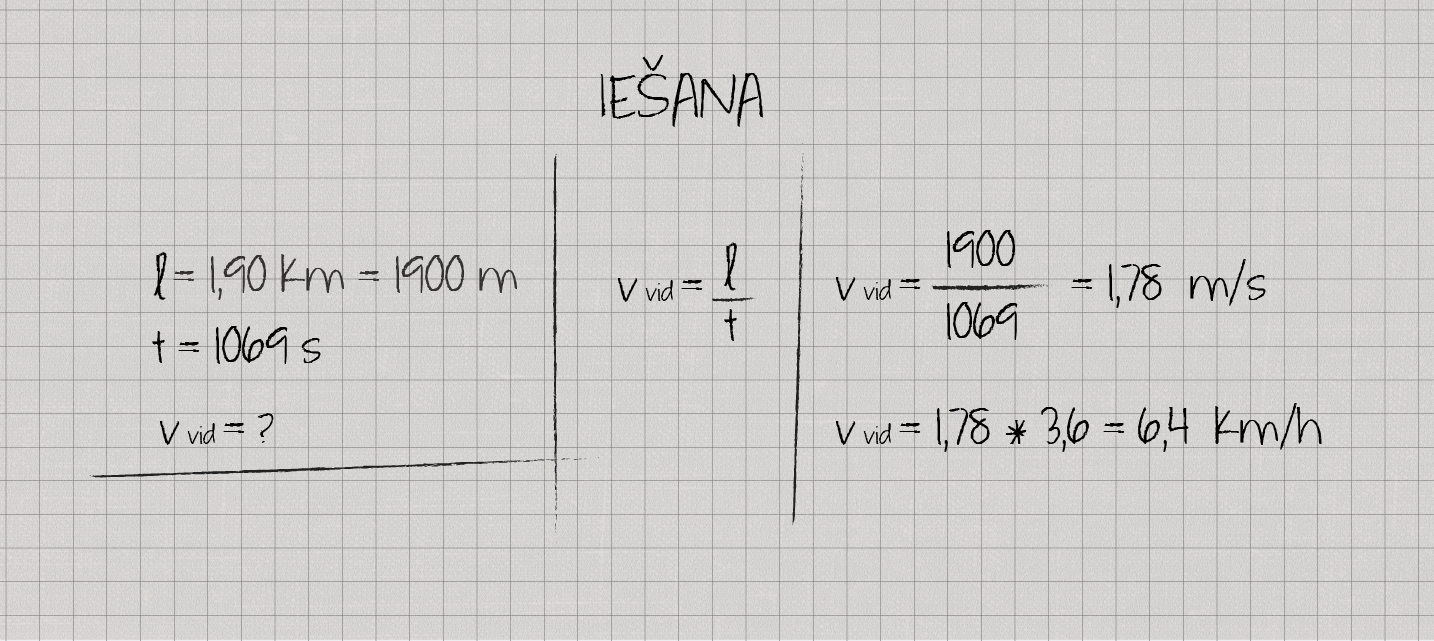
4.att. Netiešās mērīšanas piemērs pētījumā
Pētījumā iesaistīts ievērojams skaits skalāru lielumu (5. att.), tomēr lielākā daļa no tiem pētījuma laikā ir fiksēti vai arī tie ir nenozīmīgi pētījumā veikšanai. Piemēram, nobrauktais attālums l ir fiksēts lielums, jo ar katru pārvietošanās veidu ir jāveic viens un tas pats attālums, lai rezultātus varētu salīdzināt.

5.att. Skalāri lielumi
Protams, pētījumā nevar iztikt arī bez vektoriāliem lielumiem, piemēram, automašīnas paātrinājuma a, smaguma spēka FG u. c. (6. att.).
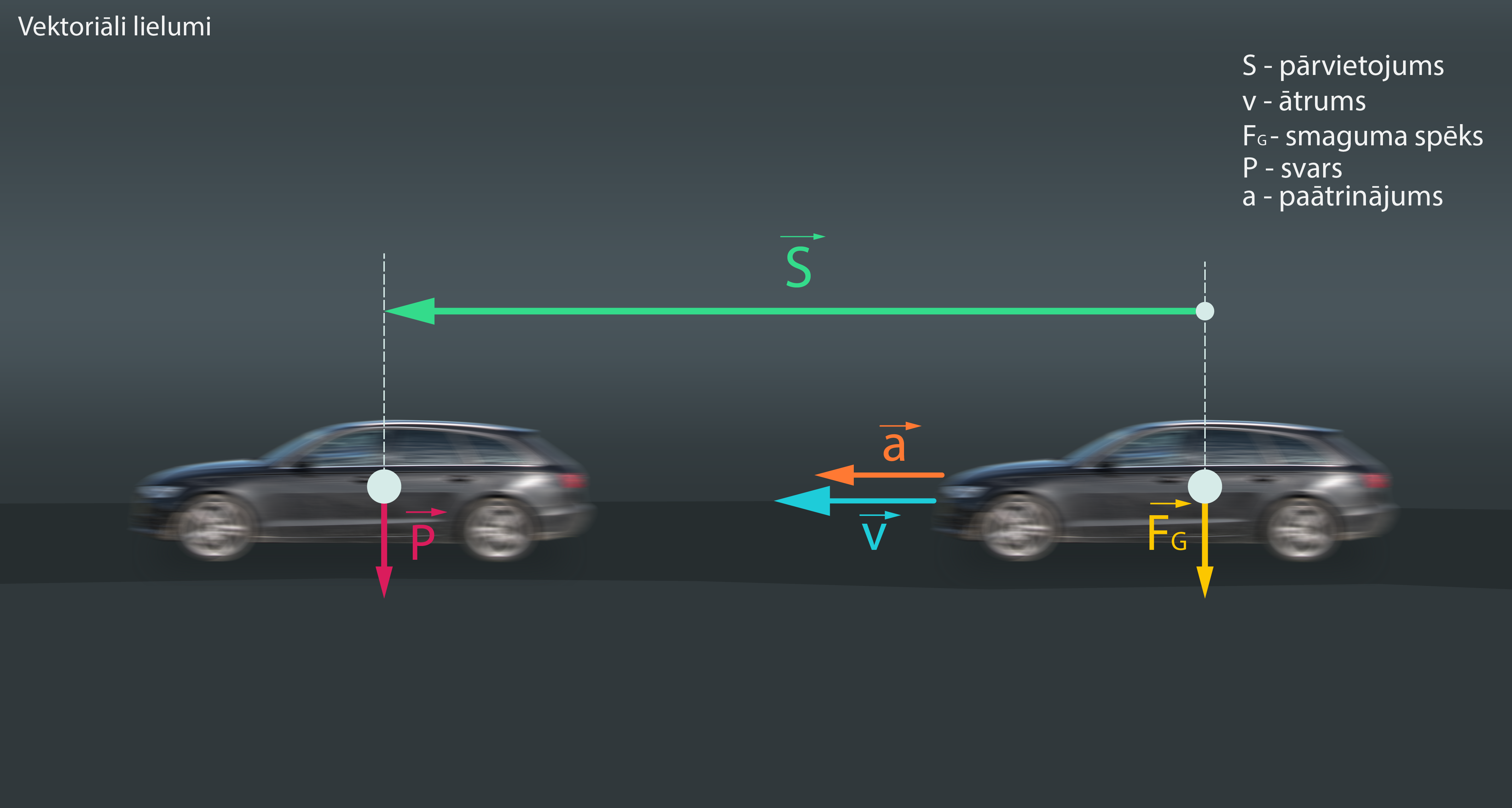
6.att. Vektoriāli lielumi
SI sistēmas nelietošana var dažkārt arī dārgi izmaksāt. Piemēram, 1998. gadā uz Marsu tika nosūtīts 338 kilogramus smagais kosmiskais aparāts Mars Climate Orbiter (1. att.), lai pētītu šīs planētas klimatu. Pirms aparāts paspēja ieiet orbītā ap Marsu, ar to pazuda sakari, līdz ar to vadību pārņēma aparāta borta dators, taču tas, kā izrādījās, nedarbojās ar datiem SI sistēmā, kā tas bija nepieciešams. Gala rezultātā kosmiskais aparāts pietuvojās pārāk tuvu planētai un sadalījās. Zaudējumi bija vairāk nekā 500 miljonu EUR apmērā.

1.att. Kosmiskais aparāts Mars Climate Orbiter