Automobilis velk piekabi pa taisnu horizontālu ceļu. Automobiļa masa ir \(m_1=1200\space\mathrm{kg}\), piekabes masa ir \(m_2=700\space\mathrm{kg}\). Automobilis kopā ar piekabi kustas ar paātrinājumu \(a=2\space\mathrm{m/s^2}\).
Aprēķini sakabes sastiepuma spēku, neievērojot pretestības spēkus! Parādi aprēķinu gaitu!
Uzdevumā ķermeņi, kas savienoti ar sakabi, kustas kopā horizontālajā virzienā. Uz katru no diviem ķermeņiem darbojas spēki, kas piešķir gan automobilim, gan piekabei paātrinājumu \(\overrightarrow{a}\). Abi ķermeņi pārvietojas ar vienādu paātrinājumu.
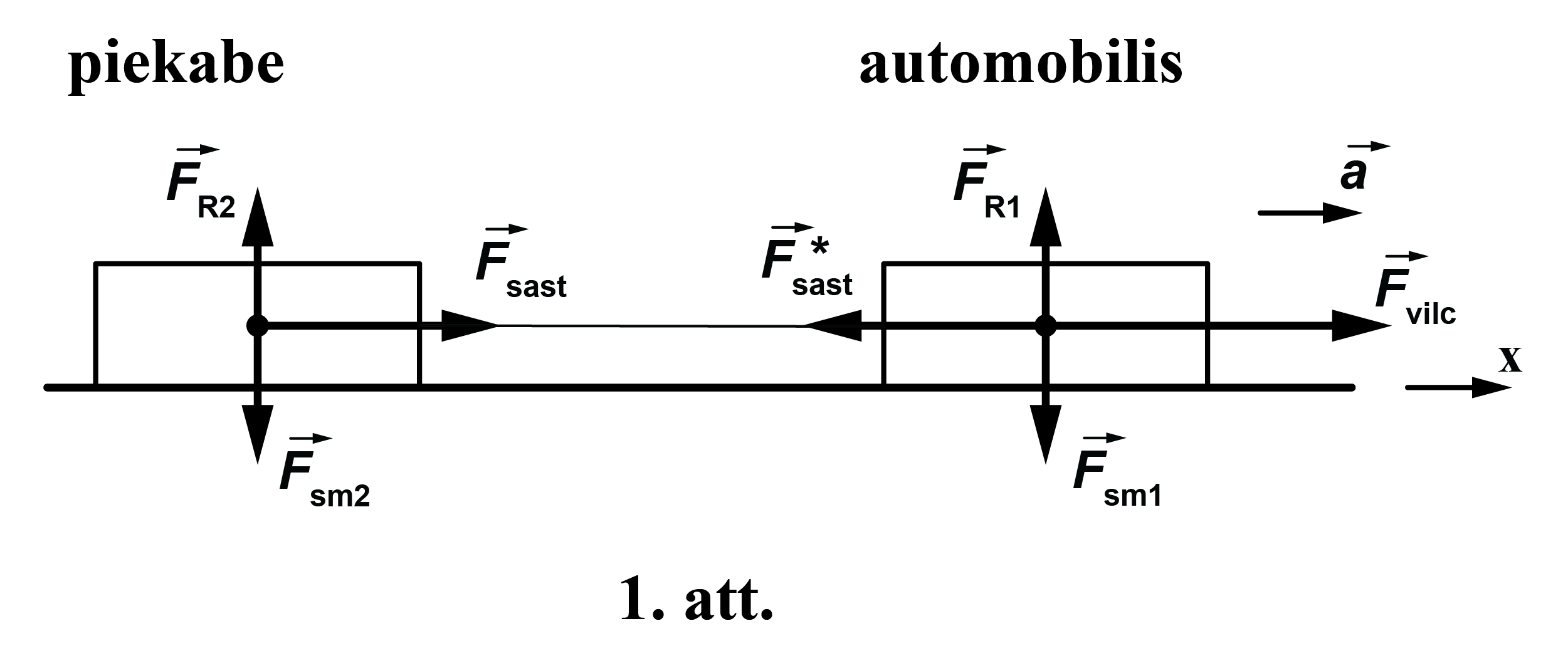
Uz automobili (skatīt 1. attēlu) darbojas četri spēki – vilcējspēks \(\overrightarrow{F}_{\mathrm{vilc}}\), smaguma spēks \(\overrightarrow{F}_{\mathrm{sm1}}\), balsta reakcijas spēks \(\overrightarrow{F}_{\mathrm{R1}}\), sakabes sastiepuma spēks \(\overrightarrow{F}_{\mathrm{sast}}^*\). Uz piekabi darbojas trīs spēki - sakabes sastiepuma spēks \(\overrightarrow{F}_{\mathrm{sast}}\), smaguma spēks \(\overrightarrow{F}_{\mathrm{sm2}}\), balsta reakcijas spēks \(\overrightarrow{F}_{\mathrm{R2}}\). Saskaņā ar III Ņūtona likumu abi sastiepuma spēki \(\overrightarrow{F}_{\mathrm{sast}}^*\) un \(\overrightarrow{F}_{\mathrm{sast}}\) pēc moduļiem ir vienādi.
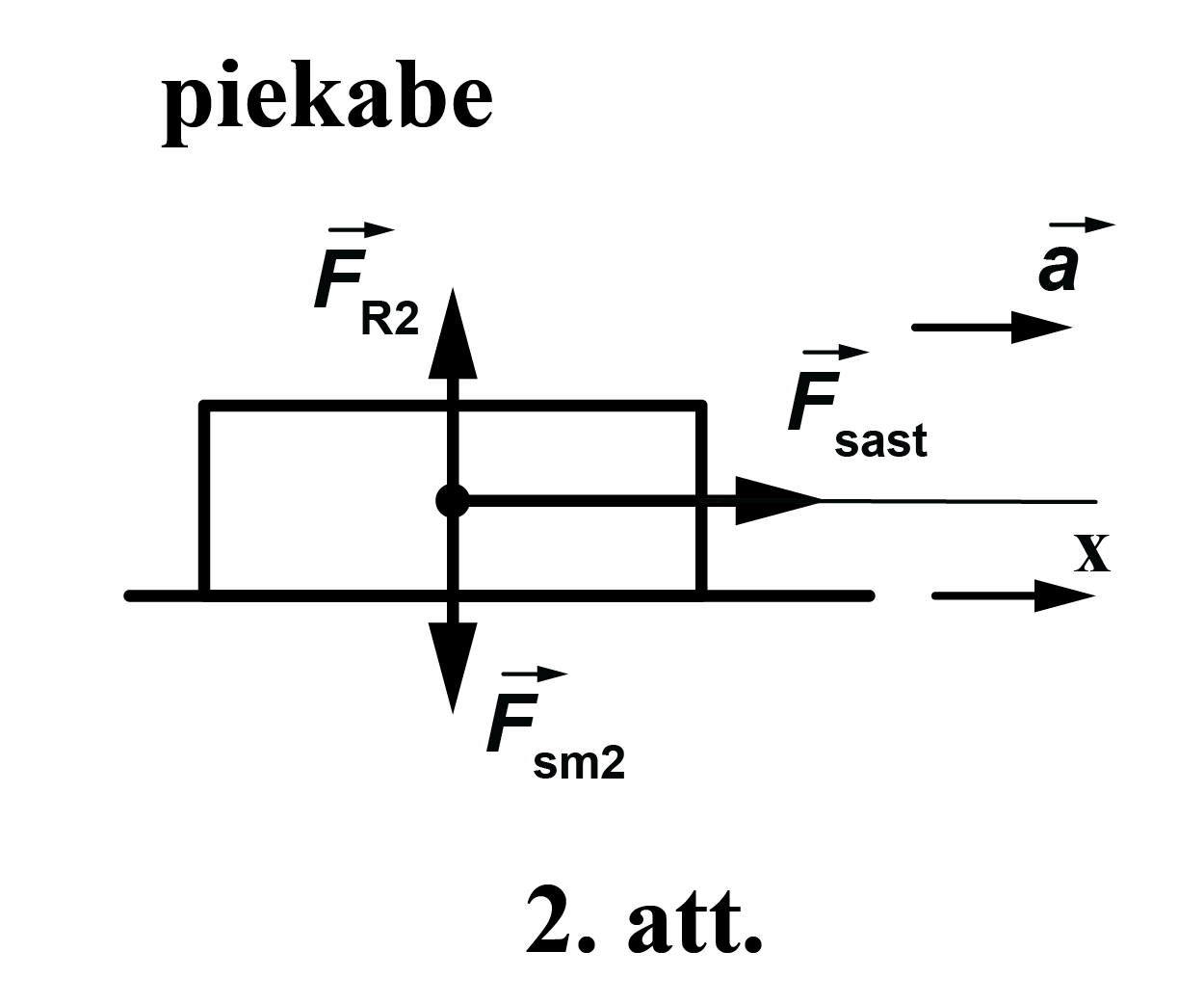
Ja aplūko tikai piekabes kustību (skatīt 2. attēlu), tad ir redzams, ka kustības virzienā uz piekabi darbojas tikai sastiepuma spēks \(\overrightarrow{F}_{\mathrm{sast}}\).
Uzrakstot II Ņūtona likuma formulu piekabes kustībai projekcijās uz X ass: \({F}_{\mathrm{sast}}=m_2a\), nosaka sakabes sastiepuma spēku:
\({F}_{\mathrm{sast}}=m_2a=700\cdot2=1400\space\mathrm{N}\)
No uzdevuma analīzes ir redzams, ka automobiļa masa risinājumā nav jāizmanto.
Atbilde: sakabes sastiepuma spēks ir \(1400\space\mathrm{N}\).
Vērtēšanas kritēriji:
Izmanto otro Ņūtona likumu sakabes sastiepuma spēka aprēķināšanai – 1 punkts.
Aprēķina sastiepuma spēku un pieraksta rezultātu ar mērvienību – 1 punkts.