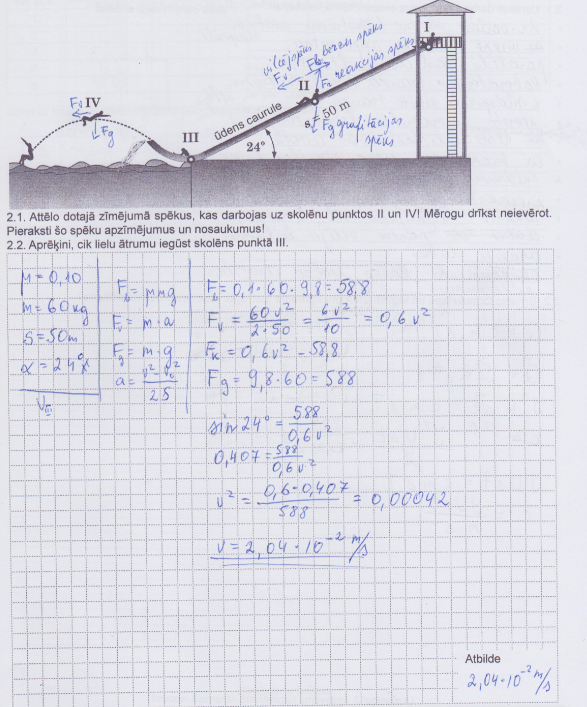
Skolēns, kura masa ir 60 kg, punktā I uzsāk slīdēt pa cauruli. Punktā III viņš sasniedz caurules zemāko punktu, bet punktā IV skolēns sasniedz brīvā lidojuma augstāko trajektorijas punktu. Berzes koeficients starp skolēnu un cauruli ir 0,10. Gaisa pretestību neņem vērā!
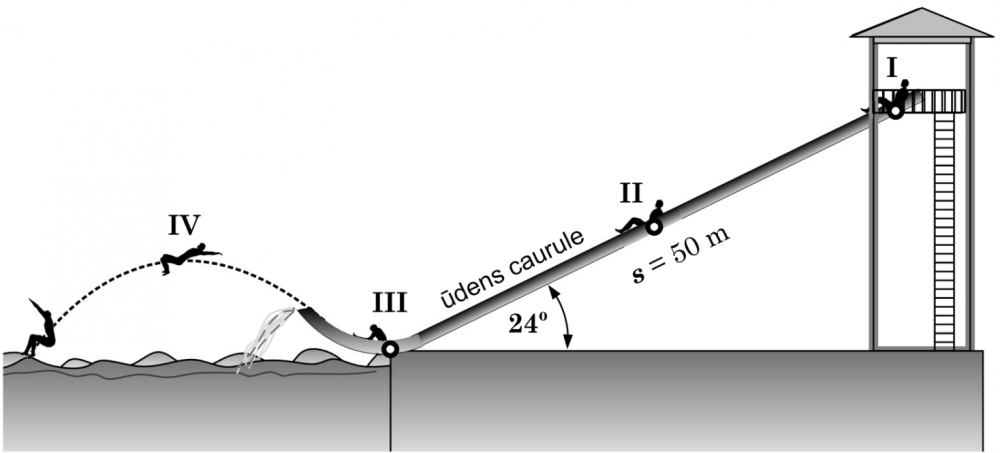
2.1. Attēlo dotajā zīmējumā spēkus, kas darbojas uz skolēnu punktos II un IV! Mērogu drīkst neievērot. Pieraksti šo spēku apzīmējumus un nosaukumus!
2.2. Aprēķini, cik lielu ātrumu iegūst skolēns punktā III.
2.1. Punktā II uz skolēnu darbojas trīs spēki: smaguma spēks \(\overrightarrow{F}_{\mathrm{sm}}\) vertikāli uz leju, caurules reakcijas spēks \(\overrightarrow{F}_{\mathrm{R}}\) perpendikulāri caurulei un slīdes berzes spēks \(\overrightarrow{F}_{\mathrm{b}}\) pretēji kustības virzienam (1. att.).
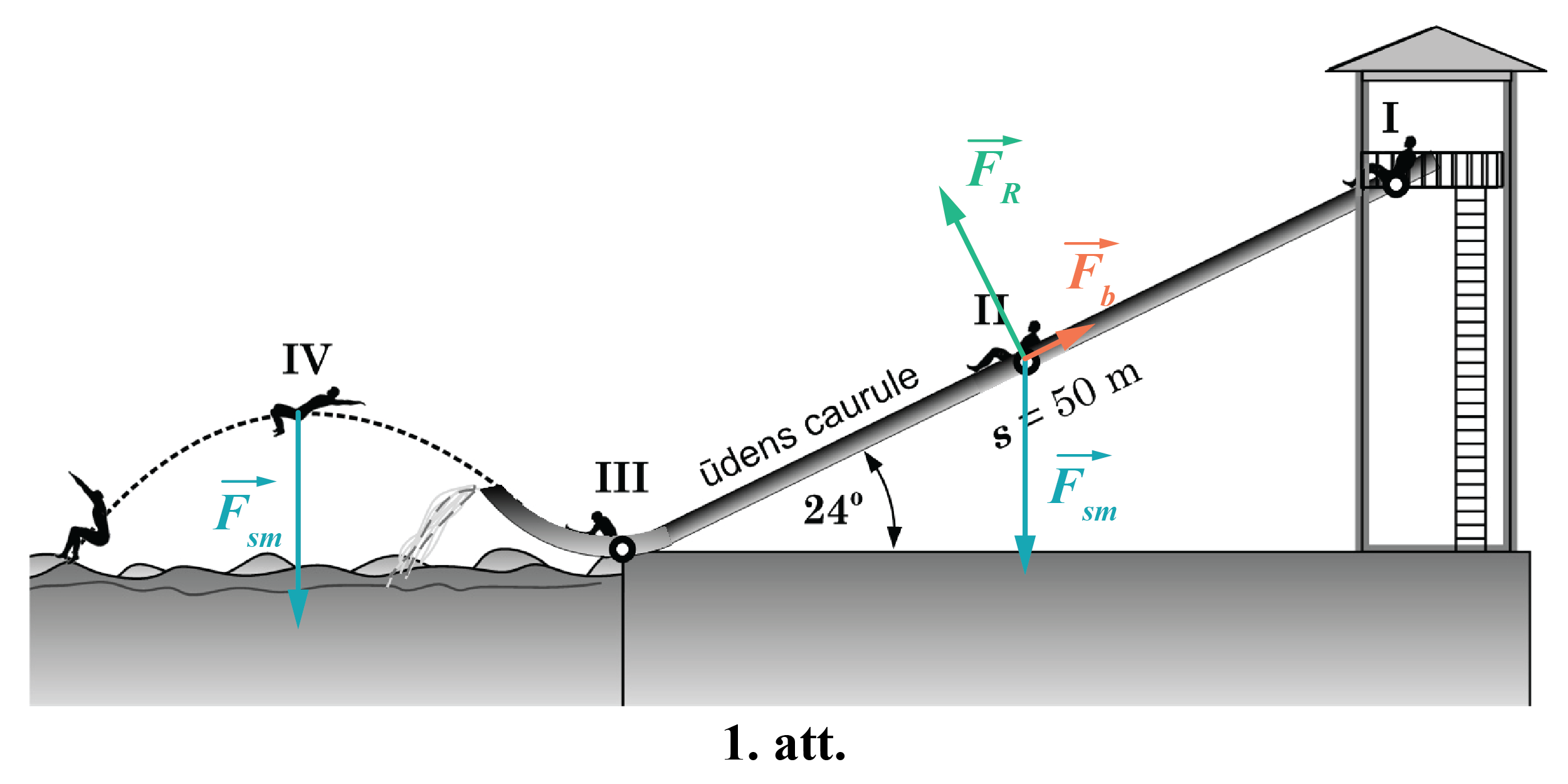
Punktā IV uz skolēnu darbojas tikai viens spēks: smaguma spēks \(\overrightarrow{F}_{\mathrm{sm}}\) vertikāli uz leju (1. att.). Uzdevuma tekstā ir teikts, kā gaisa pretestību neņem vērā.
2.2. Skolēna ātrumu punktā III var noteikt, izmantojot spēkus (dinamiskā metode) vai enerģijas nezūdamības likumu (enerģētiskā metode).
Izmantotie apzīmējumi: \(m\) – skolēna masa, \(g\) – brīvās krišanas paātrinājums, \(h\) – augstums virs punkta III līmeņa, \(v\) – skolēna ātrums punktā III, \(\mu\) – slīdes berzes koeficients starp skolēnu un cauruli, \(\alpha\) – caurules leņķis attiecībā pret horizontu.
1. Dinamiskā metode:
Skolēna ātrumu \(v\) punktā III nosaka pēc formulas \(v^2-v_0^2=2as\). No uzdevuma teksta ir zināms, ka punktā I sākuma ātrums \(v_0=0\). Tāpēc \(v=\sqrt{2as}\). Kustības paātrinājums nav vienāds ar brīvās krišanas paātrinājumu un tas ir jāatrod no II Ņūtona likuma.
Kustības laikā no punkta I līdz punktam III uz skolēnu darbojas trīs spēki \(\overrightarrow{F}_{\mathrm{sm}}\), \(\overrightarrow{F}_{\mathrm{R}}\) un \(\overrightarrow{F}_{\mathrm{b}}\) (2. att.). Rezultējošais spēks \(\overrightarrow{F}_{\mathrm{rez}}\) piešķir skolēnam paātrinājumu saskaņā ar II Ņūtona likumu \(\overrightarrow{F}_{\mathrm{rez}}=m\overrightarrow{a}\) vai \(\overrightarrow{F}_{\mathrm{sm}}+\overrightarrow{F}_{\mathrm{R}}+\overrightarrow{F}_{\mathrm{b}}=m\overrightarrow{a}\).
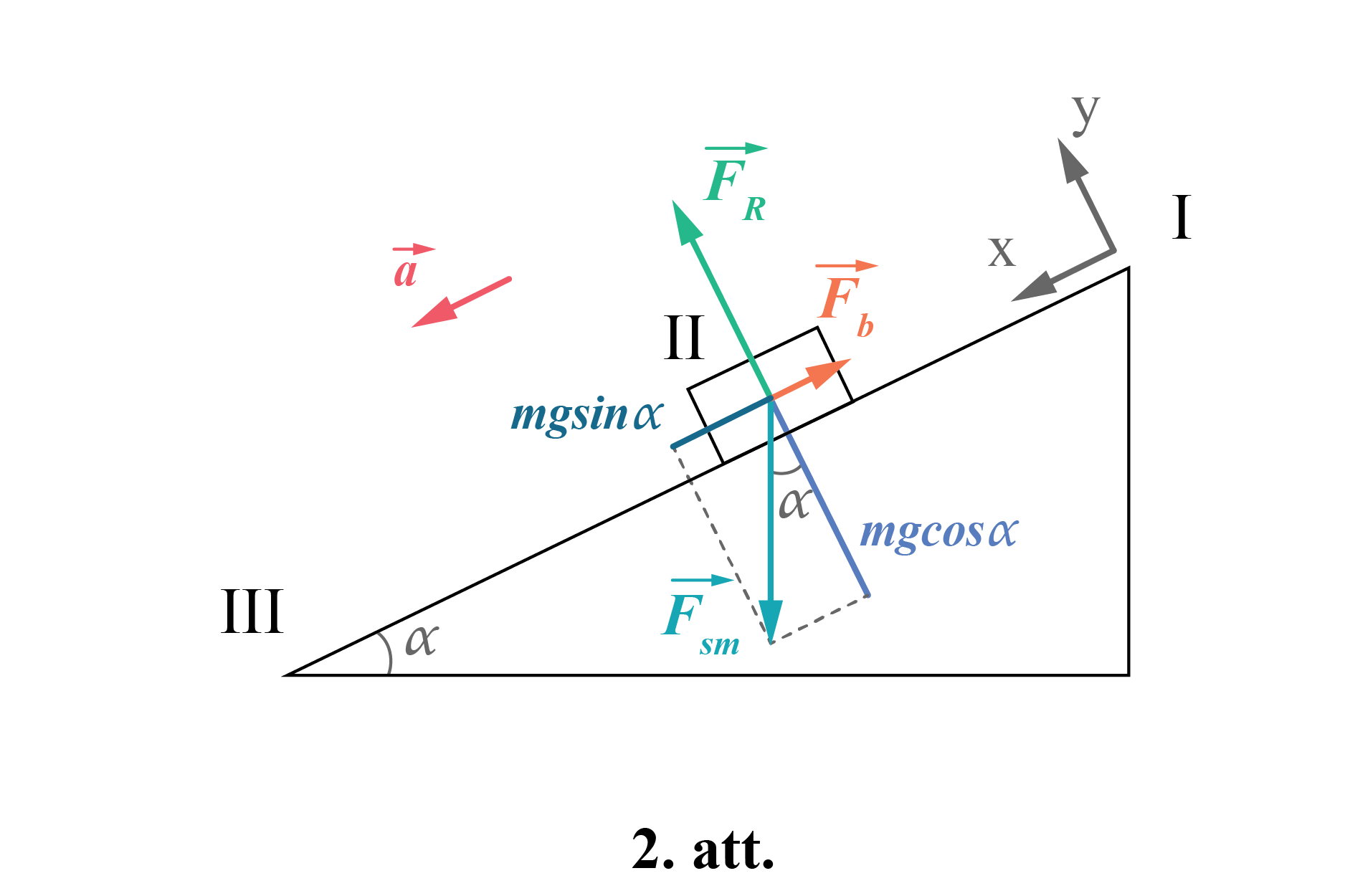
Vienādojuma projekcijas uz koordinātu asīm:
Uz X ass: \(mg\sin\alpha-F_{\mathrm{b}}=ma\) (1).
Uz Y ass: \(F_{\mathrm{R}}-mg\cos\alpha=0\) (2).
Slīdes berzes spēks \(F_{\mathrm{b}}=\mu F_{\mathrm{R}}\).
No vienādojuma (2) nosaka caurules reakcijas spēku \(F_{\mathrm{R}}=mg\cos\alpha\) un iegūst slīdes berzes spēka aprēķina formulu \(F_{\mathrm{b}}=\mu mg\cos\alpha\) un ievieto vienādojumā (1):
\(mg\sin\alpha-\mu mg\cos\alpha=ma\).
Tālāk saīsina ar \(m\) un izsaka paātrinājumu \(a=g(\sin\alpha-\mu\cos\alpha)\).
Skolēna ātrums punktā III ir vienāds ar \(v=\sqrt{2as}=\sqrt{2gs(\sin\alpha-\mu\cos\alpha)}\).
Aprēķini:
\(v=\sqrt{2gs(\sin\alpha-\mu\cos\alpha)}=\sqrt{2\cdot 10\cdot 50\cdot(\sin{24^{\mathrm{o}}-0,10\cos{24^{\mathrm{o}}}})}\approx17,9\space\mathrm{m/s}\approx 18\space\mathrm{m/s}\).
Aprēķini pa soļiem:
Skolēna smaguma spēks \(F_{\mathrm{sm}}=mg=60\cdot 10=600\space\mathrm N\).
Caurules reakcijas spēks \(F_{\mathrm{R}}=mg\cos\alpha=60\cdot 10\cdot\cos24^{\mathrm{o}}\approx548\space\mathrm{N}\).
Slīdes berzes spēks \(F_{\mathrm{b}}=\mu F_{\mathrm{R}}=0,10\cdot548=54,8\space\mathrm{N}\).
Skolēna smaguma spēka projekcija kustības virzienā \(mg\sin\alpha=60\cdot10\cdot\sin24^{\mathrm{o}}\approx244\space\mathrm{N}\).
Skolēna kustības paātrinājums caurulītē \(a=\frac{mg\sin\alpha-F_{\mathrm{b}}}{m}=\frac{244-54,8}{60}\approx3,15\space\mathrm{m/s^2}\).
Skolēna ātrums III punktā \(v=\sqrt{2as}=\sqrt{2\cdot3,15\cdot 50}\approx17,7\space\mathrm{m/s}\approx18\space\mathrm{m/s}\).
2. Enerģētiskā metode:
Punktā I skolēnam piemīt pilnā mehāniskā enerģija, kas iekļauj tikai potenciālo enerģiju \(W_{\mathrm{p}}=mgh\), Kustības laikā potenciālā enerģija pāriet kinētiskajā enerģijā \(W_{\mathrm{kin}}=\frac{mv^2}{2}\) un tiek pastrādāts darbs \(A\) slīdes berzes spēka pārvarēšanai. Tā kā pilnā mehāniskā enerģija saglabājas visu kustības laiku, tad \(W_{\mathrm{pot}}=W_{\mathrm{kin}}+A\).
Darbu \(A\) berzes spēka pārvarēšanai nosaka pēc formulas \(A=F_{\mathrm{b}}s\). Slīdes berzes spēku nosaka no izteiksmes \(F_{\mathrm{b}}=\mu F_{\mathrm{R}}\). Savukārt balsta reakcijas spēku aprēķina pēc formulas \(F_{\mathrm{R}}=mg\cos\alpha\).
Augstumu \(h\) nosaka no taisnleņķa trijstūra h= s·sinα.
Ievieto visas sakarības formulā \(W_{\mathrm{pot}}=W_{\mathrm{kin}}+A\), iegūst izteiksmi \(mgs\sin\alpha=\frac{mv^2}{2}+\mu mgscos\alpha\). Tālāk aprēķina skolēna ātrumu punktā III: \(v=\sqrt{2gs(\sin\alpha-\mu\cos\alpha)}\).
Piezīme: Aprēķinus var veikt pa soļiem. Var arī izmantot citas formulas aprēķiniem.
Aprēķini:
Skolēna potenciālā enerģija punktā I: \(W_{\mathrm{pot}}=mgh=mgs\sin\alpha=60\cdot 10\cdot50\cdot\sin 24^{\mathrm{o}}\approx12202\space\mathrm{J}\).
Darbs slīdes berzes spēka pārvarēšanai \(A=F_{\mathrm{b}}s=54,8\cdot 50=2740\space\mathrm{J}\).
Skolēna kinētiskā enerģija punktā III: \(W_{\mathrm{kin}}=W_{\mathrm{pot}}-A=12202-2740=9462\space\mathrm{J}\).
Skolēna ātrums punktā III: \(v=\sqrt{\frac{2W_{\mathrm{kin}}}{m}}=\sqrt{\frac{2\cdot9462}{60}}\approx17,8\space\mathrm{m/s}\approx18\space\mathrm{m/s}\).
Atbilde: Skolēna ātrums punktā III ir \(18\space\mathrm{m/s}\) .
Vērtēšanas kritēriji:
1. Dināmiskā metode:
Attēlo spēkus punktā II un IV un pieraksta to apzīmējumus un nosaukumus – 1 punkts.
Aprēķina smaguma spēka projekciju un balsta reakcijas spēku – 1 punkts.
Aprēķina slīdes berzes spēku – 1 punkts.
Aprēķina kustības paātrinājumu – 1 punkts.
Aprēķina ātrumu – 1 punkts.
2. Enerģētiskā metode:
Attēlo spēkus punktā II un IV un pieraksta to apzīmējumus un nosaukumus – 1 punkts.
Aprēķina potenciālo enerģiju – 1 punkts.
Aprēķina berzes spēka darbu – 1 punkts.
Aprēķina kinētisko enerģiju – 1 punkts.
Aprēķina ātrumu punktā III – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri:
1. piemērs: Risinājums novērtēts ar 5 punktiem.
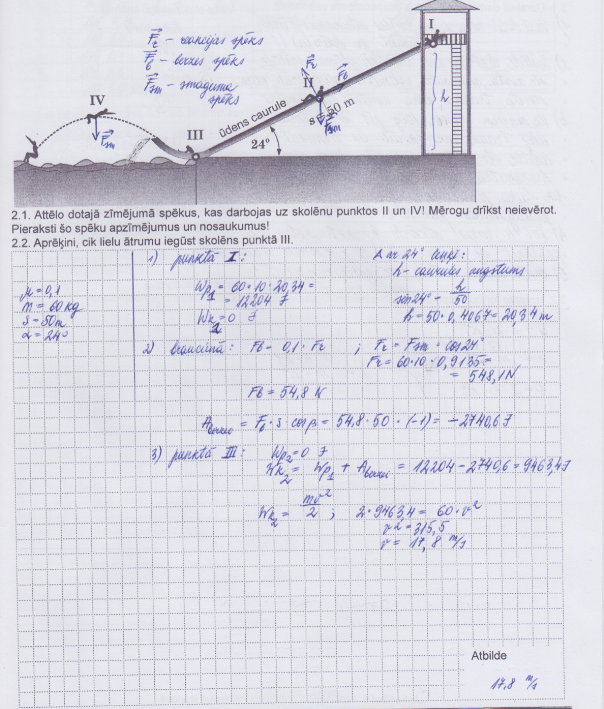
2. piemērs: Risinājums novērtēts ar 5 punktiem.
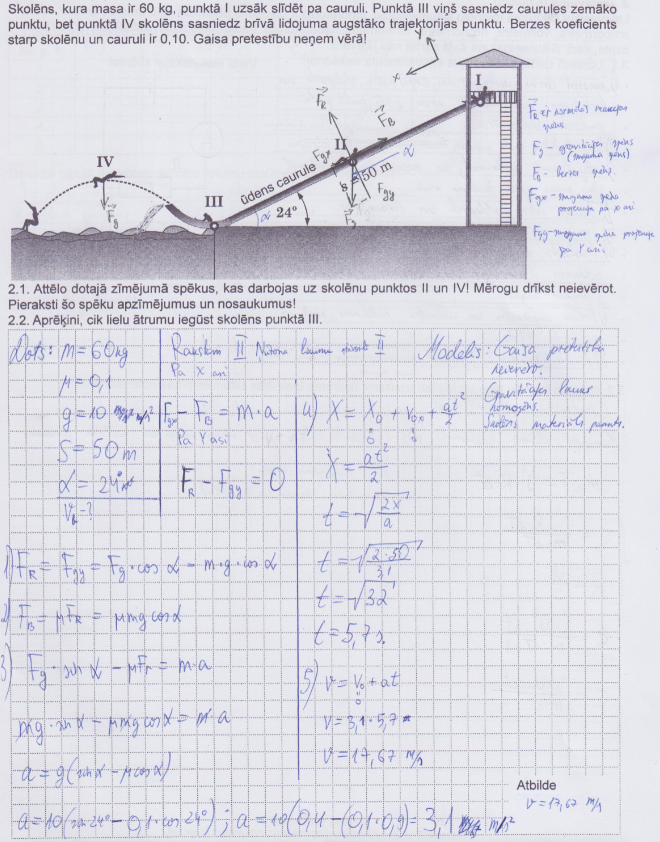
3. piemērs: Risinājums novērtēts ar 4 punktiem - nepareizi noteikts berzes spēks.
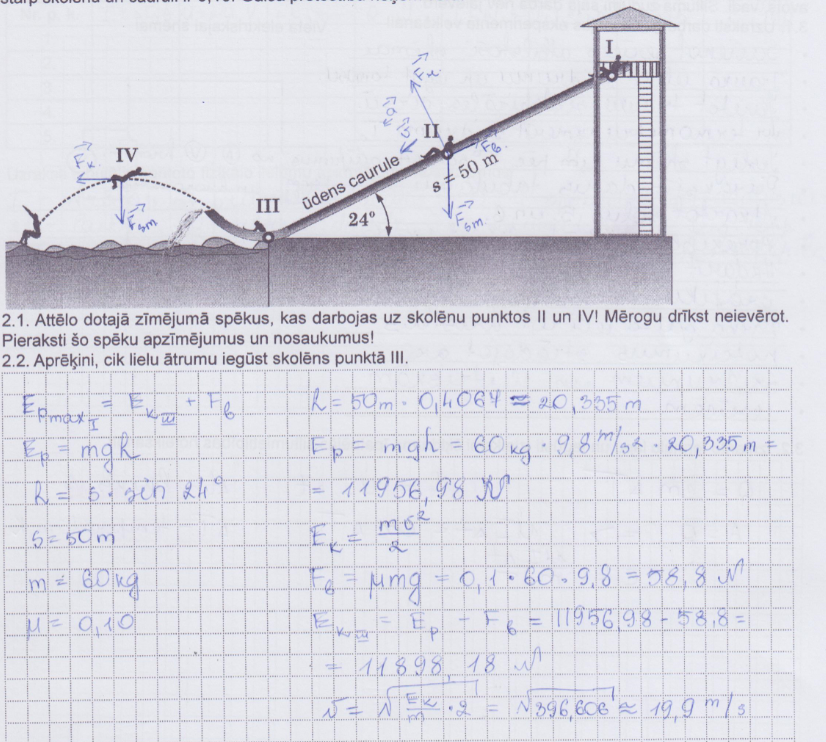
4. piemērs: Risinājums novērtēts ar 3 punktiem - nav noteikts ātrums un paātrinājums.
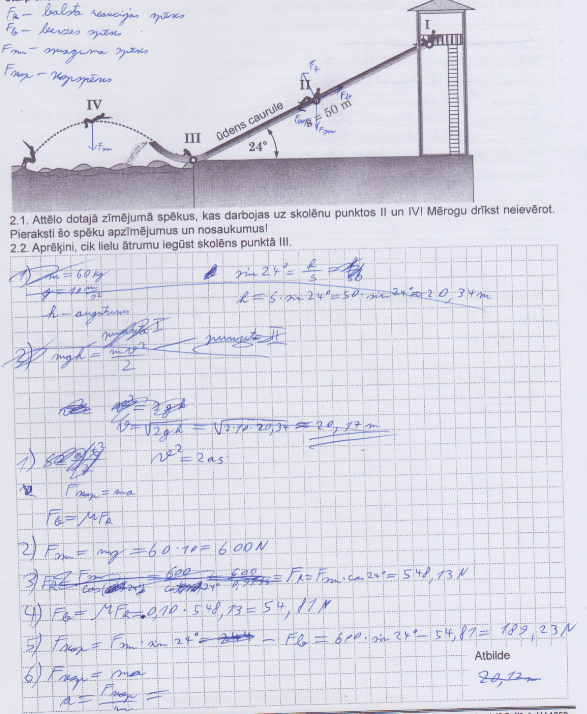
5. piemērs: Risinājums novērtēts ar 0 punktiem.