Lāsteka bez berzes slīd pa slīpu virsmu, kas ar horizontu veido leņķi α. Lāsteka uzsāk slīdēt augstumā H. Brīvās krišanas paātrinājums ir g. Cik liels ir lāstekas ātrums \(v\), kad tā ir veikusi pusceļu? Atbildi pamato! Izmanto tikai dotos apzīmējumus!
Uzdevumu var risināt, izmantojot gan enerģijas nezūdamības likumu, gan vienmērīgi paātrinātas kustības likumsakarības.
Pirmais risinājuma variants:
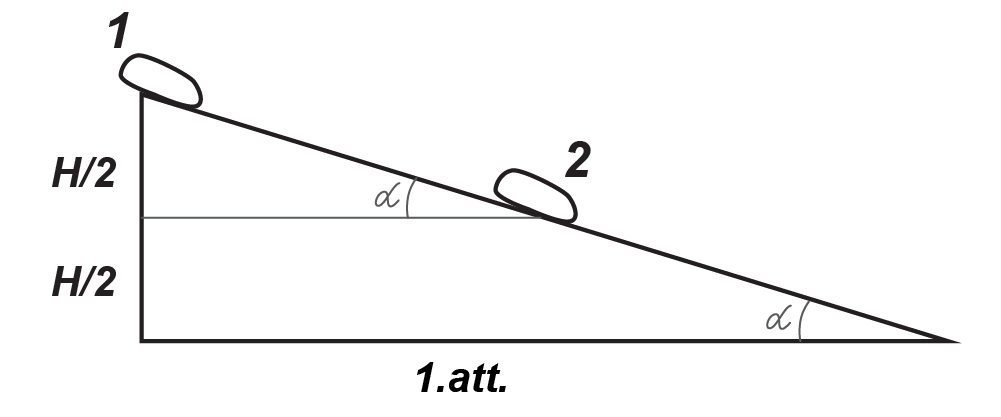
Punktā 1 lāstekas (1. att.) sākuma ātrums ir vienāds ar nulli. Kad lāsteka ir veikusi pusceļu, tā atrodas punktā 2. Zīmējumā no punkta 2 novelk taisni paralēli slīpās virsmas pamatnei. Leņķis starp taisni un slīpo virsmu ir α, tātad, veidojas divi līdzīgi trijstūri. Kad lāsteka ir veikusi pusceļu, tā atrodas punktā 2. Tā kā lāsteka sāk salīdēt no augstuma H, tad veicot pusceļu, tās augstums ir H/2.
Pēc uzdevuma nosacījumiem, lāsteka slīd bez berzes, tapēc tās pilnā mehāniskā enerģija nemainās. Par potenciālās enerģijas nulles līmeni izvēlēsimies lāstekas stāvokli punktā 2. Punktā 1 lāstekai attiecībā pret punktu 2 piemīt potenciālā enerģija \(E_{\mathrm{pot}}=mg\frac{H}{2}\). Savukārt, punktā 2 lāstekai piemīt tikai kinētiskā enerģija \(E_{\mathrm{kin}}=\frac{mv^2}2\). Pēc pilnās mehāniskās enerģijas nezūdamības likuma, lāstekas potenciālā enerģija punktā 1 vienāda ar kinētisko enerģiju punktā 2:
\(E_{\mathrm{pot}}=E_{\mathrm{kin}}\space \) jeb \(\space mg\frac{H}{2}=\frac{mv^2}{2}\). No dotā vienādojuma izsakot lāstekas kustības ātrumu \(v\) punktā 2, iegūst: \(v=\sqrt{gH}\).
Otrais risinājuma variants:
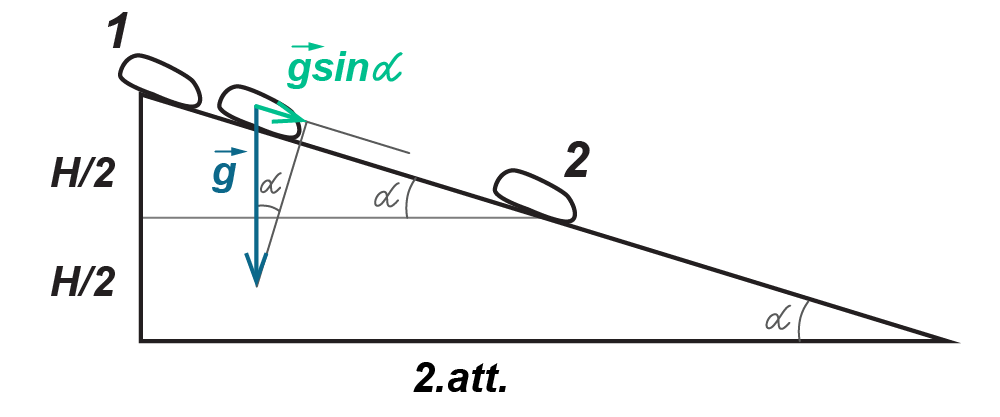
Lāstekas kustība pa slīpo virsmu bez berzes ir vienmērīgi paātrināta kustība ar paātrinājumu \(a=g\sin{\alpha}\) (2. att.). Lāstekas veikto ceļu \(S\) starp punktiem 1 un 2 var noteikt, izmantojot sakarības taisnleņķa trijstūrī:
\(\sin \alpha =\frac{H}{2s} \space \implies \space s=\frac{H}{2 \sin \alpha}\)
Lāstekas ātruma aprēķināšanai punktā 2 izmanto formulu \(v^2- v_0^2=2as\), kur \(a \) ir lāstekas paātrinājums, \(s\) - lāstekas veiktais ceļš, \(v_0\) - lāstekas sākuma ātrums, kas šajā situācijā ir vienāds ar nulli. Ievietojot formulā izteiksmes paātrinājuma un veiktā ceļa noteikšanai, iegūst:
\(v^2=2 \cdot g \sin \alpha \cdot \frac{H}{2 \cdot \sin \alpha}\), no kurienes \(v= \sqrt{gH}\).
Atbilde: Lāstekas kustības ātrums pusceļā ir \(v= \sqrt{gH}\)
Vērtēšanas kritēriji
I variants
Iegūst sakarību starp veikto ceļu un augstumu vai citādāk pamato, ka, veicot pusceļu, lāstekas augstums samazinās 2 reizes – 1 punkts.
Izmanto mehāniskās enerģijas nezūdamības likumu – 1 punkts.
Iegūst gala izteiksmi ātruma aprēķināšanai – 1 punkts.
II variants
Iegūst sakarību starp veikto ceļu un augstumu vai citādāk pamato, ka, veicot pusceļu, lāstekas augstums samazinās par H/2 – 1 punkts.
Iegūst izteiksmi lāstekas paātrinājuma aprēķināšanai – 1 punkts.
Zina vai atrod formulu lapā izteiksmi, kas saista ātrumu un ceļu paātrinātā kustībā, un izsaka meklējamo lielumu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemērī
1. piemērs: risinājums novērtēts ar 3 punktiem.

2. piemērs: risinājums novērtēts ar 3 punktiem.
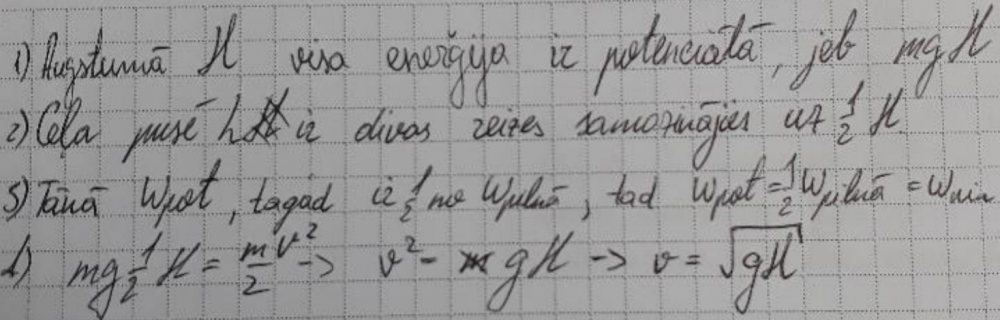
3. piemērs: risinājums novērtēts ar 3 punktiem.
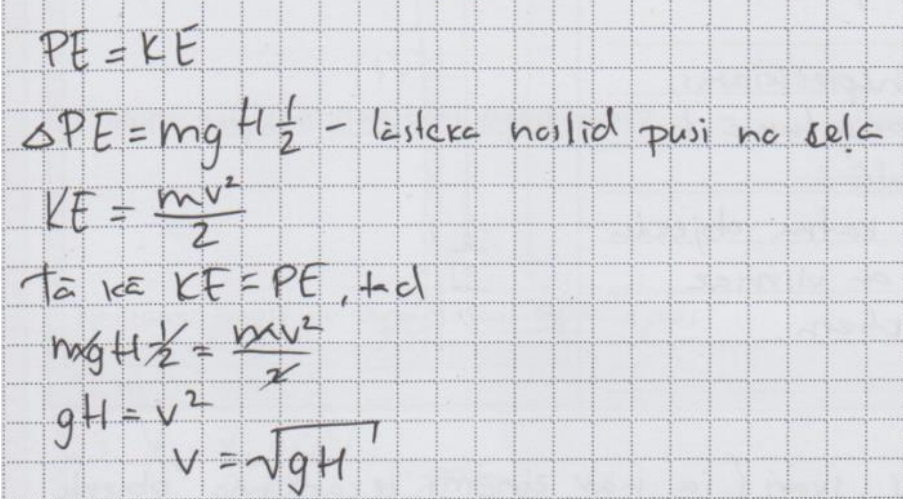
4. piemērs: risinājums novērtēts ar 2 punktiem (risināšanās ideja ir pareiza, bet kinētiskā enerģija ir divreiz mazākā).

5. piemērs: risinājums novērtēts ar 2 punktiem (lāsteka nekrīt ar brīvāš krišanas paātrinājumu).
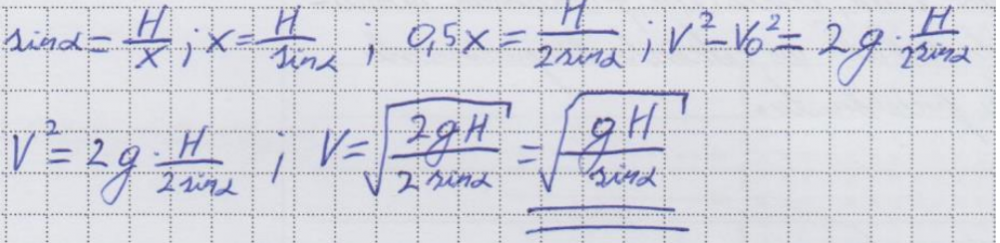
6. piemērs: risinājums novērtēts ar 1 punktu (par enerģijas likuma nezūdamības izmantošanu).
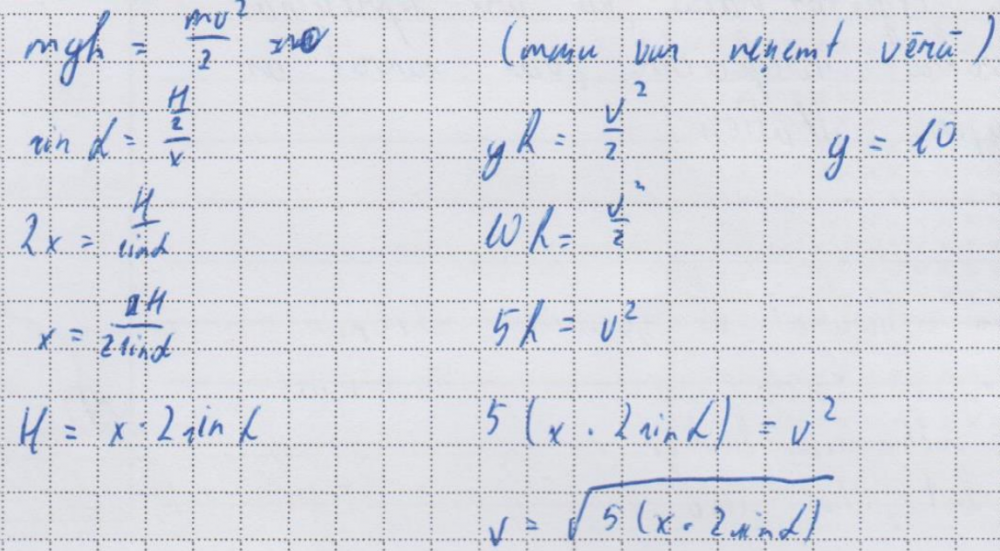
7. piemērs: risinājums novērtēts ar 1 punktu (par risinājuma plānu).

8. piemērs: risinājums novērtēts ar 1 punktu (par sakarības \(v^2-v_0^2=2as\) izmantošanu).
