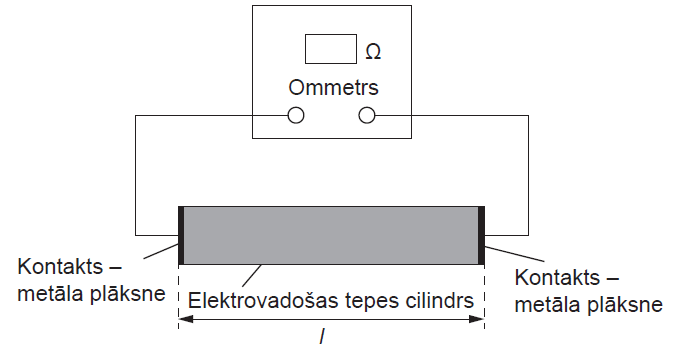
Elektrovadošā tepe (špaktele) ir mīksts materiāls, kuram var viegli piešķirt dažādas formas. Lai noskaidrotu, kā noteikta tilpuma tepes gabala pretestība mainās atkarībā no tā garuma, veica eksperimentu un aprēķināja materiāla īpatnējo pretestību. Elektrovadošās tepes cilindra garuma \(l\) un ar ommetru izmērītās pretestības \(R\) vērtības dotas uzdevuma 2. punkta tabulā. Pretestības mērījumu kļūda ir neievērojami maza.
Ir zināms, ka elektrovadošās tepes cilindra īpatnējo pretestību \(\rho\) nosaka pēc formulas \(\rho=\frac{(R-R_0)V}{l^2}\), kur \(R_0\)ir savienojošo vadu un kontaktu pretestība, \(V\)ir elektrovadošās tepes gabala tilpums, bet \(l\)– tā garums.
1. Pamato, kāpēc \(R\) atkarības no \(l^2\) attēlošana grafikā ļautu pamatot formulā doto sakarību starp \(R\) un \(l\)!
2. Aprēķini un ieraksti tabulā \(l^2\) vērtības un \(l^2\) absolūtās kļūdas vērtības! Norādi aprēķinos izmantotās izteiksmes un aprēķina piemēru!
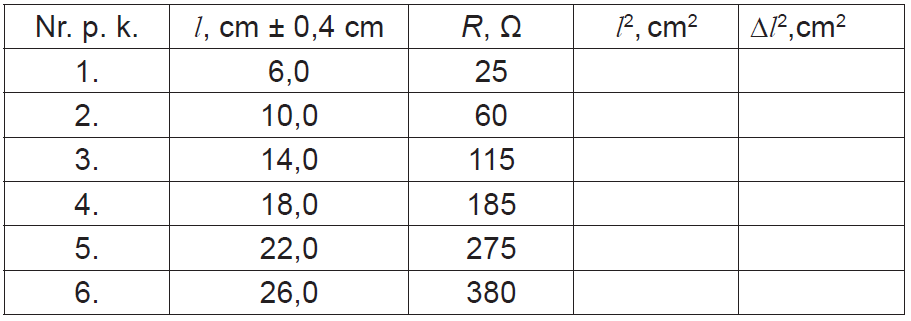
Mērījumu un aprēķinu tabula
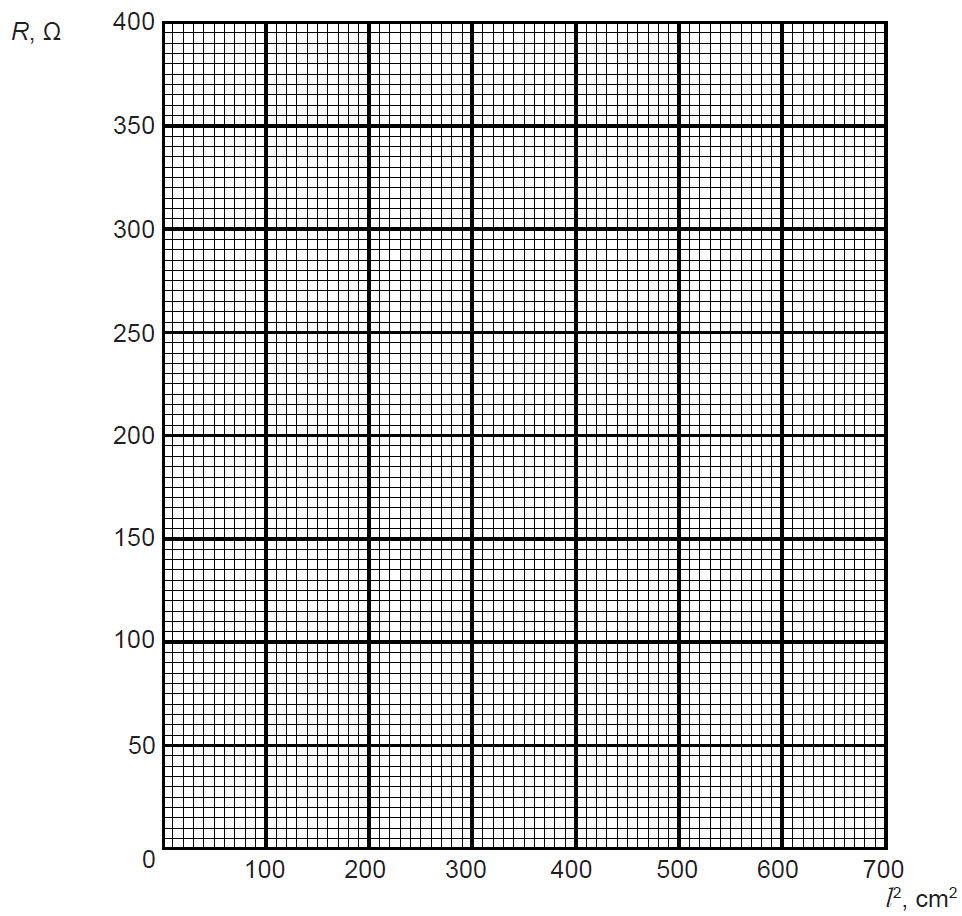
3. Uzzīmē \(R\) atkarības no \(l^2\) grafiku!
4. Nosaki iegūtās taisnes virziena (slīpuma) koeficientu!
5. Skaidro, kā, izmantojot iegūto grafiku, iespējams noteikt īpatnējās elektriskās pretestības \(\rho\) vērtību!
6. Izmantotā elektrovadošās tepes gabala tilpums ir 18,8 cm3. Nosaki īpatnējās elektriskās pretestības \(\rho\) vērtību!
7. Kādu vēl informāciju par eksperimenta iekārtu var iegūt, izmantojot šo grafiku? Atbildi pamato!
1. punkts. Pamato, kāpēc \(R\) atkarības no \(l^2\) attēlošana grafikā ļautu pamatot formulā doto sakarību starp \(R\) un \(l\)!
Uzdevumā prasīts, kā pretestības \(R\) atkarības no \(l^2\) attēlošana grafikā ļauj (palīdz) pamatot doto sakarību starp \(R\) un \(l\). Acīmredzot, doto sakarību – formulu ir jāpārveido tā, lai būtu skaidri saskatāma \(R\) atkarība no \(l\) (vai, kā sagaidāms no \(l^2\)) – tātad, jāizsaka \(R\).
Pārveidojot formulu un izsakot \(R\) atkarību no \(l^2\), iegūst:
\(R=\frac{\rho}{V}l^2+R_0\)
No matemātikas zināms, ka šādas sakarības grafiks ir taisne (\(y=kx+b\)).
Tātad, ja iegūtās \(R\) atkarības no \(l^2\) grafiks būtu taisne, formulā dotā sakarība varētu būt pareiza. Šo secinājumu var papildināt ar spriedumu no fizikas – izmantojot datu bukletā atrodamo pretestības formulu \(R=\frac{\rho l}{S}\) var secināt, ka iegūtā sakarība šai pretestības formulai atbilst: ievietojot iepriekš iegūtajā sakarībā izteiksmi cilindra tilpuma aprēķināšanai \(V=lS\), iegūst:
\(R=\frac{\rho}{V}l^2+R_0=R=\frac{\rho}{lS}l^2+R_0=R=\frac{\rho}{S}l+R_0\).
Fakts, ka grafikam jābūt taisnei, atrodams arī uzdevuma 4. punkta formulējumā.
ATBILDE
Pārveidojot formulu un izsakot \(R\) atkarību no \(l^2\), iegūst:
\(R=\frac{\rho}{V}l^2+R_0\). Šādas sakarības grafiks ir taisne (\(y=kx+b\)). Tātad, ja pētījumā iegūto datu grafiks būtu taisne, formulā dotā sakarība varētu būt pareiza.
2. punkts. Aprēķini un ieraksti tabulā \(l^2\) vērtības un \(l^2\) absolūtās kļūdas vērtības! Norādi aprēķinos izmantotās izteiksmes un aprēķina piemēru!
\(l^2\) aprēķins šaubas nerada – tabulā dotā \(l\) vērtība jākāpina kvadrātā, piemēram \(l^2=6,0\cdot6,0=36\space\mathrm{cm^2}\).
Lai aprēķinātu lieluma \(l^2\) absolūto kļūdu var izmantot datu bukletā atrodamo informāciju:
Jāpiebilst, ka datu bukletā trūkst informācijas par to, ka otro metodi var izmantot tikai gadījumā, ja lielumi \(a\) un \(b\) ir savstarpēji neatkarīgi, kas nozīmē, ka situācijai \(l^2=l\cdot l\) tā piemērojama nav. Tātad, šoreiz der tikai pirmā metode. Var izmantot arī ievietošanas paņēmienu – aprēķināt \(l\) parciālo kļūdu un pēc tam rezultējošo kļūdu.
ATBILDE
\(l^2=6,0\cdot6,0=36\space\mathrm{cm^2}\)
\(\Delta(l^2)=l^2\cdot2\frac{\Delta l}{l}=6,0^2\cdot2\cdot\frac{0,4}{6,0}=4,8\space\mathrm{cm^2}\)
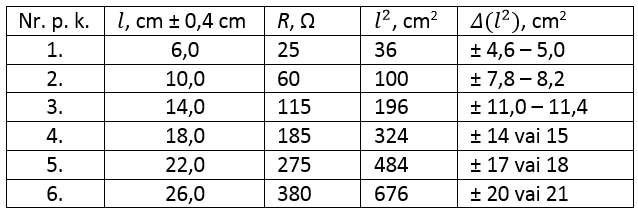
3. punkts. Uzzīmē \(R\) atkarības no \(l^2\) grafiku!
Jau 1. punktā konstatēts, ka \(R\) atkarības no \(l^2\) grafiks varētu būt taisne (\(\mathrm{y=kx+c}\)).
\(R=\frac{\rho}{V}l^2+R_0\)
Fakts, ka grafikam jābūt taisnei, atrodams 4. punkta formulējumā.
Ja \(R_0\neq0\), šai taisnei nav jāiet caur koordinātu sākumpunktu.
Iepriekšējā uzdevumā aprēķinātas \(\Delta(l)^2\) vērtības, ko jāizmanto, grafiku veidojot. Uzdevuma tekstā teikts arī, ka pretestības \(R\) mērījumu kļūdas ir neievērojami mazas.
Tātad, "labā" grafikā ir:
- pareizi atlikti datu punkti
- kļūdu nogriežņi (var nebūt precīzi)
- grafiks – taisne (puslīdz "labākās atbilstības līnija")
- taisne nav "ar spēku" izvilkta caur koordinātu sākumpunktu
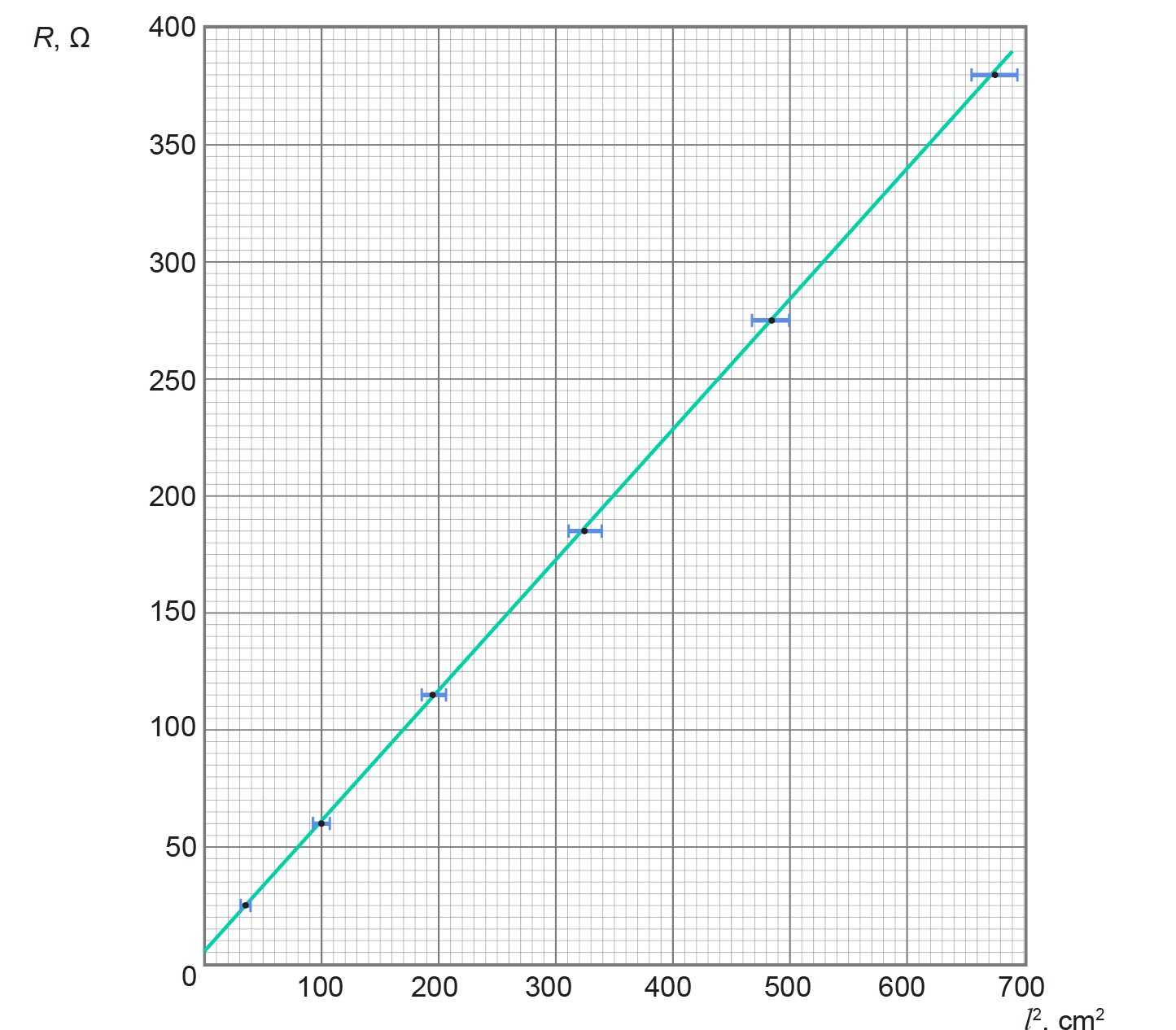
4. punkts. Nosaki iegūtās taisnes virziena (slīpuma) koeficientu!
Funkciju \(\mathrm{y=kx+c}\), kur \(\mathrm{k}\) un \(\mathrm{c}\space\in\space\mathbb{R}\), sauc par lineāru funkciju. Lineāras funkcijas grafiks ir taisne.
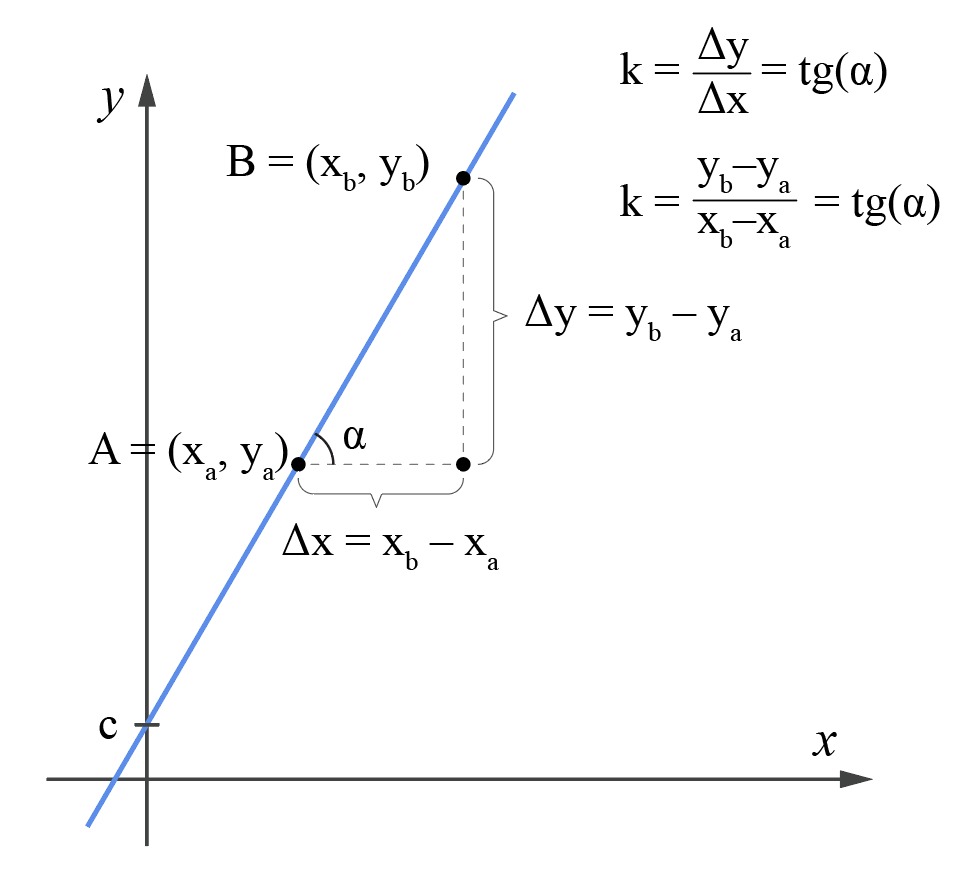
Konstante \(\mathrm{k}\) ir taisnes \(\mathrm{y=kx+c}\) virziena koeficients, \(\mathrm{k=tg\alpha}\) un konstante \(\mathrm{c}\) rāda taisnes krustpunktu ar \(\mathrm{y}\) asi.
Lai atrisinātu uzdevumu, jāizvēlas uz iepriekšējā uzdevumā zīmētās taisnes divus punktus (vēlams tādus, kas neatrodas tuvu viens otram), un jāveic atbilstošos aprēķinus.
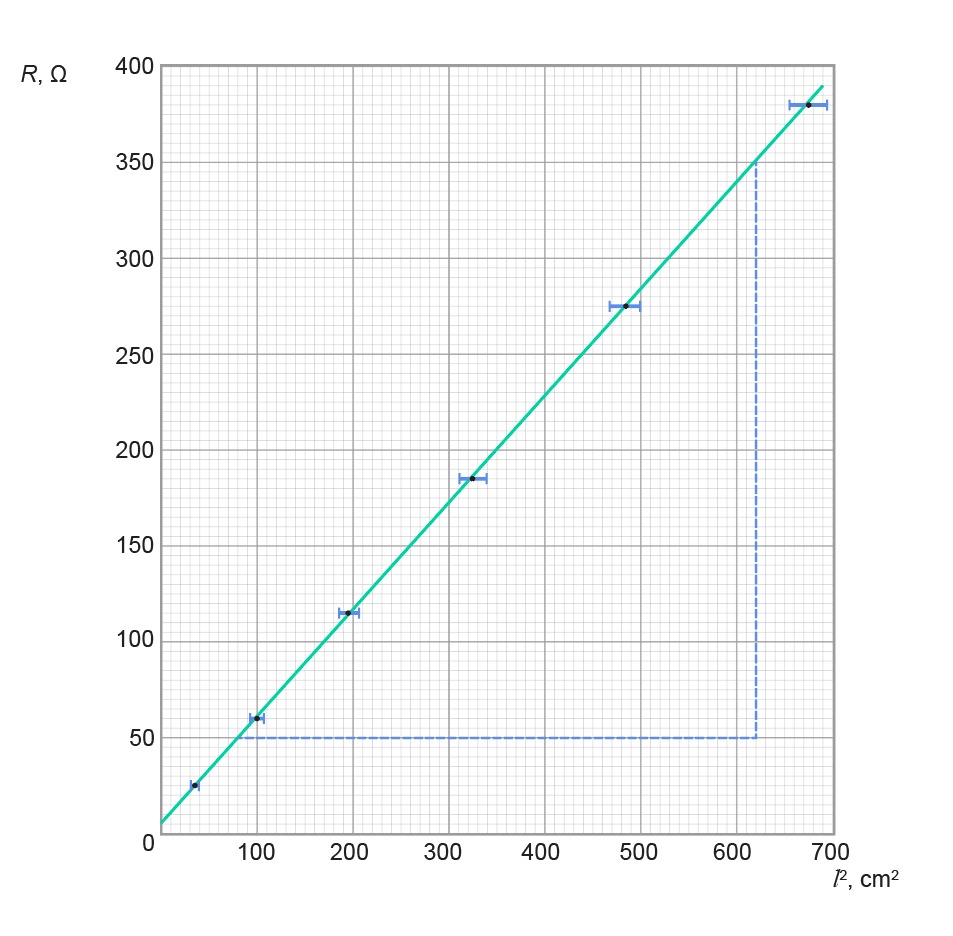
ATBILDE
\(k=\frac{R_2-R_1}{l_2^2-l_1^2}=\frac{350-50}{620-80}=0,555\space\mathrm{\Omega/cm^2}\).
5. punkts. Skaidro, kā, izmantojot iegūto grafiku, iespējams noteikt īpatnējās elektriskās pretestības \(\rho\) vērtību!
Pārveidojot uzdevumā doto sakarību un izsakot \(R\) atkarību no \(l^2\) , iegūtās taisnes
\(R=\frac{\rho}{V}l^2+R_0\) virziena koeficients \(\mathrm{k}=\frac{\rho}{V}\).
Tātad \(\rho=\mathrm{k}V\)
6. punkts. Izmantotā elektrovadošās tepes gabala tilpums ir \(18,8\space\mathrm{cm^3}\). Nosaki īpatnējās elektriskās pretestības \(\rho\) vērtību!
Izmantojot 5. punkta atrisinājumu zināms, ka īpatnējās pretestības vērtību var aprēķināt, ja zina taisnes virziena koeficientu, kas aprēķināts 4. punktā, un doto tepes gabala tilpuma vērtību.
Tad \(\rho=\mathrm{k}V=0,555\cdot18,8=10,4\space\mathrm{\Omega \cdot cm=0,104\space\Omega \cdot m}\).
Var izmantot arī uzdevumā doto sakarību \(\rho=\frac{R-R_0}{l^2}V\), ņemot datus no tabulas un \(R_0\) nolasot no taisnes krustpunkta ar \(R\) asi
(\(R_0\approx5\space\Omega\)).
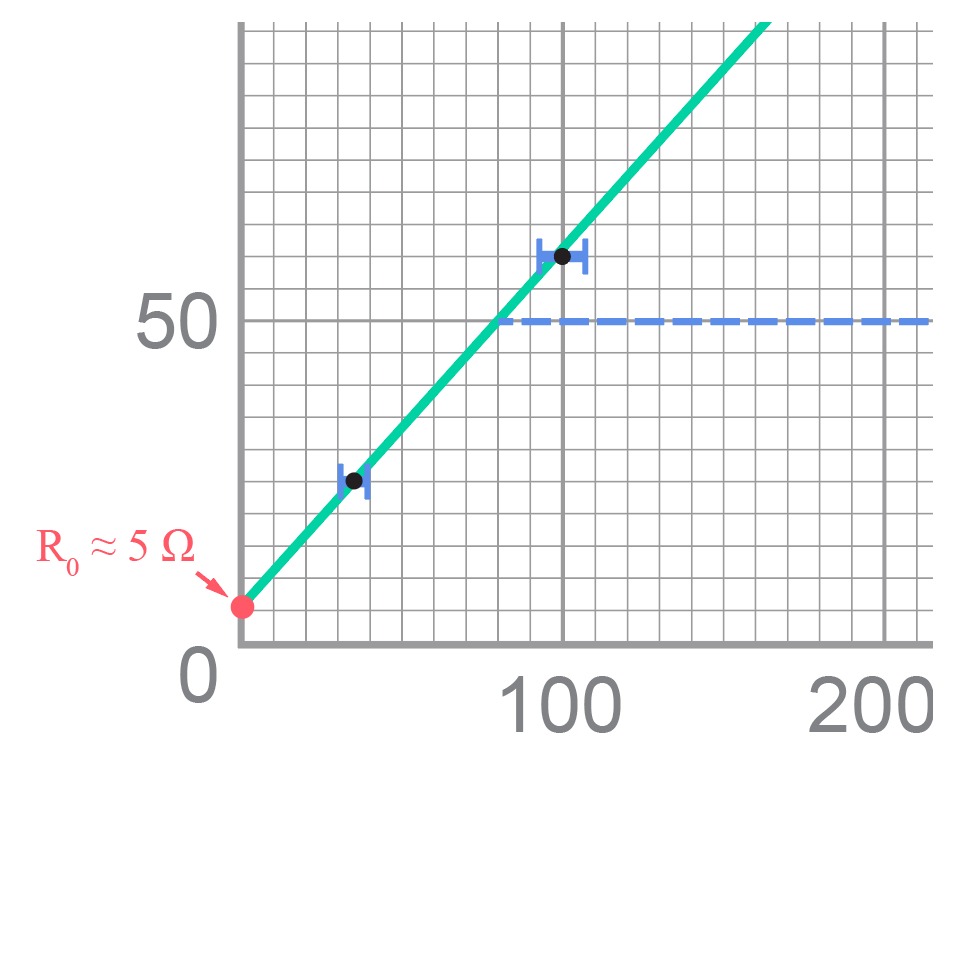7. punkts. Kādu vēl informāciju par eksperimenta iekārtu var iegūt, izmantojot šo grafiku? Atbildi pamato!
Uzdevumā jautāts, kādu informāciju var iegūt, izmantojot grafiku.
Tā kā \(R=\frac{\rho}{V}l^2+R_0\), \(R_0\) nosakāms, atrodot grafika taisnes krustpunktu ar \(\mathrm{y}(R)\) asi (\(R\) vērtība, kad \(l^2=0\)). Šajā gadījumā \(R_0\approx5\space\Omega\).
Turklāt, ja grafiks ir lineārs, var secināt, ka īpatnējā pretestība ir konstants lielums.
Šis ir komplekss uzdevums un to vērtē kopumā – vērtējot kādu konkrētu apakšuzdevumu, ņem vērā arī citos apakšuzdevumos sniegtās atbildes.
1. punkts
Uzdevuma izpilde eksāmenā – 39%.
Vērtēšanas kritēriji
Pārveido formulu, izsakot \(R\) atkarību no \(l^2\) – 1 punkts.
Secina, ka \(R\) un \(l^2\) saista lineāra sakarība – 1 punkts.
Secina, ka formulā dotā sakarība var būt patiesa, ja attēlojot datus grafiski, būs lineāra sakarība vai, ka lineāra sakarība atbilst pretestības formulai \(R=\frac{\rho l}{S}\), vai citi derīgi apsvērumi – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 3 punktiem.
3. piemērs: risinājums novērtēts ar 3 punktiem.
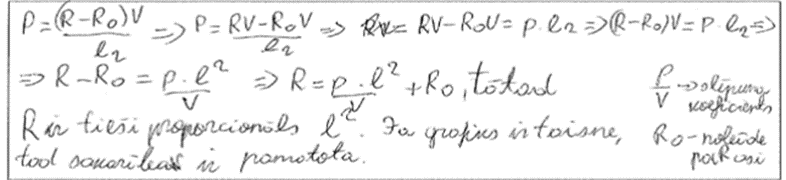
4. piemērs: risinājums novērtēts ar 3 punktiem.
5. piemērs: risinājums novērtēts ar 3 punktiem.
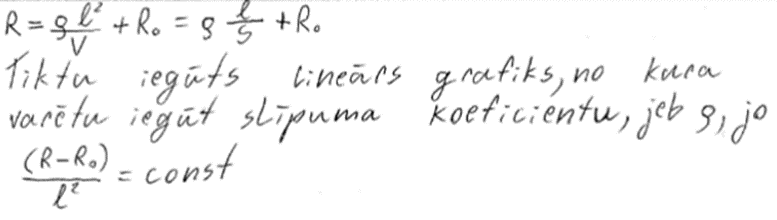
6. piemērs: risinājums novērtēts ar 2 punktiem. Sakarība nav pārveidota.
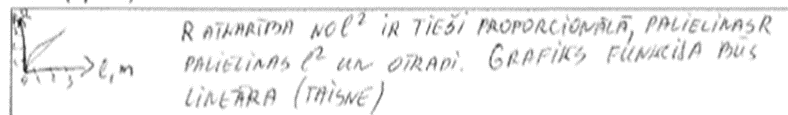
7. piemērs: risinājums novērtēts ar 2 punktiem. Sajaukts atkarīgais un neatkarīgais lielums.
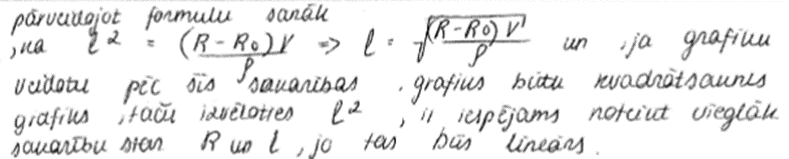
8. piemērs: risinājums novērtēts ar 1 punktu. Punkts piešķirts par ideju par taisni.
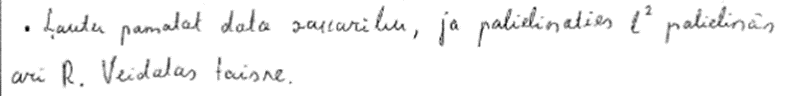
9. piemērs: risinājums novērtēts ar 1 punktu. Punkts piešķirts par ideju par taisni.
10. piemērs: risinājums novērtēts ar 0 punktu. Nav atbildes uz jautājumu.
2. punkts
Uzdevuma izpilde eksāmenā – 52%.
Aprēķina \(l^2\) (pareizi aizpildīta atbilstošā sadaļa tabulā vai tai blakus redzamas visas aprēķinātās vērtības ) – 1 punkts.
Tālāk vērtē līmeņos:
3 punkti:
Aprēķina \(l^2\) absolūto kļūdu, izmantojot relatīvo kļūdu saskaitīšanas paņēmienu, ievietošanas paņēmienu, citu derīgu metodi vai datu bukleta 2. metodi.
Ir uzrakstīta kļūdu aprēķina izteiksme un aprēķina piemērs.
Rezultāti ierakstīts tabulā, zīmīgo ciparu skaits nepārsniedz piecus.
Pieļaujama nebūtiska nepilnība.
2 punkti:
Ir viena būtiska nepilnība:
• neatbilstošs zīmīgo ciparu skaits;
• kļūdas, aprēķinā, ievietojot skaitļus;
• nepareizi pārveidota kļūdu aprēķina formula, lai izmantotu konkrētajā situācijā;
• nav parādīts, kā formula pārveidota konkrētajai situācijai, ja iegūti nepareizi skaitliski rezultāti.
1 punkts:
Vairākas nepilnības
VAI
\(l^2\) absolūtās kļūdas aprēķinātas izmantojot nepareizu formulu, piemēram \((\Delta l)^2\), bet skaitliski pareizi, pierakstot ar atbilstošu zīmīgo ciparu skaitu.
0 punktu:
\(l^2\) absolūtās kļūdas aprēķina nav vai tā rēķināta kā gadījuma kļūda.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem.
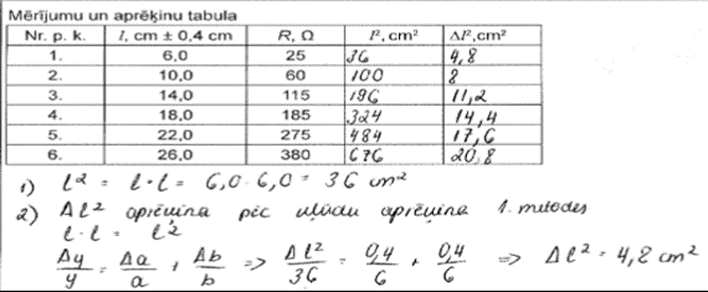
2. piemērs: risinājums novērtēts ar 4 punktiem. Kļūdas novērtējums maksimāls, bet pamatots.
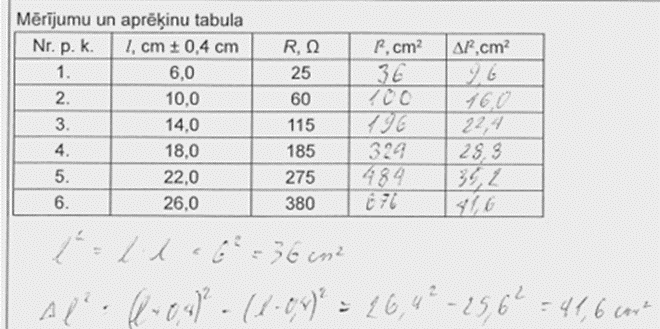
3. piemērs: risinājums novērtēts ar 3 punktiem. It kā tikai divreiz mazāks rezultāts, bet nav rādīts, kā to formulu iegūst...
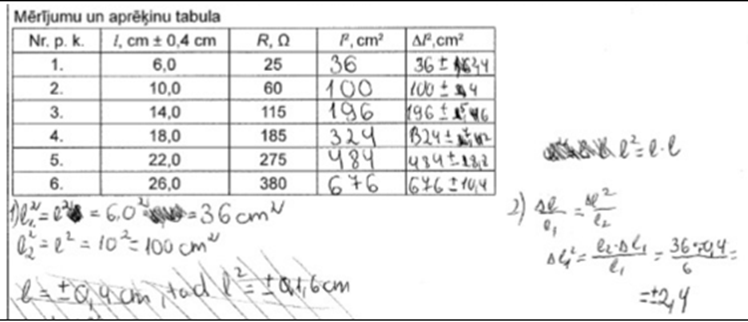
4. piemērs: risinājums novērtēts ar 2 punktiem. Nederīga metode kļūdas aprēķinam, bet, saskaņā ar vērtēšanas kritērijiem, 1 punktu piešķir.
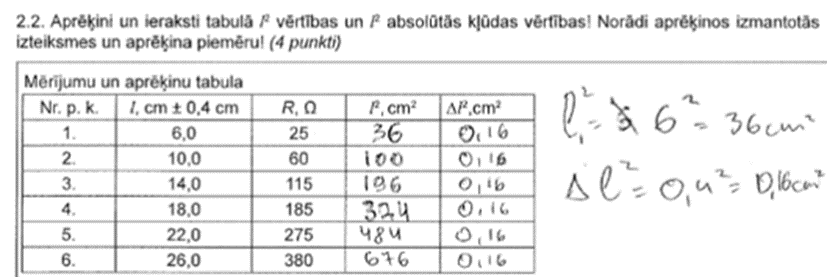
5. piemērs: risinājums novērtēts ar 1 punktu.
3. punkts
Uzdevuma izpilde eksāmenā – 73%.
Vērtē līmeņos.
2 punkti, ja ir izpildīti vismaz trīs no:
• pareizi atlikti datu punkti;
• atbilstoši aprēķinātajām kļūdām \(\Delta(l)^2\) parādīti kļūdu nogriežņi (var nebūt precīzi);
• grafiks – taisne (labākās atbilstības līnija);
• grafiks nav datu punktiem neatbilstoši izvilkts caur koordinātu sākumpunktu.
1 punkts, ja ir divas nepilnības.
0 punktu, ja ir trīs vai vairāk nepilnības.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
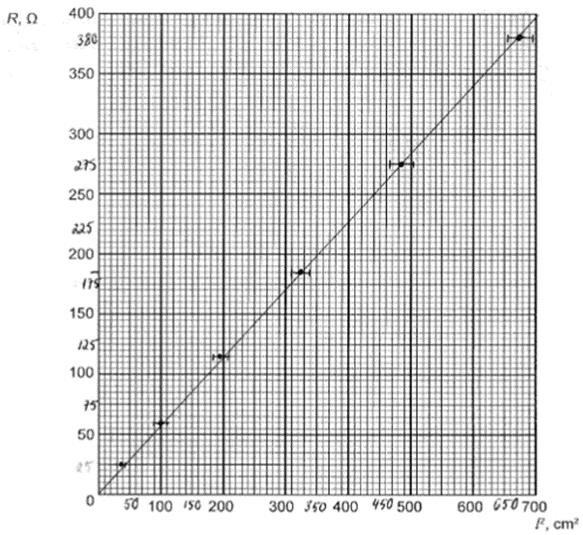
2. piemērs: risinājums novērtēts ar 1 punktu. Grafiks ir datu punktiem neatbilstoši izvilkts caur koordinātu sākumpunktu.
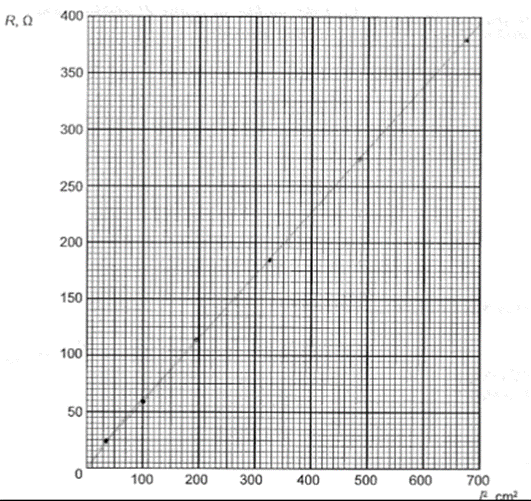
3. piemērs: risinājums novērtēts ar 0 punktu.
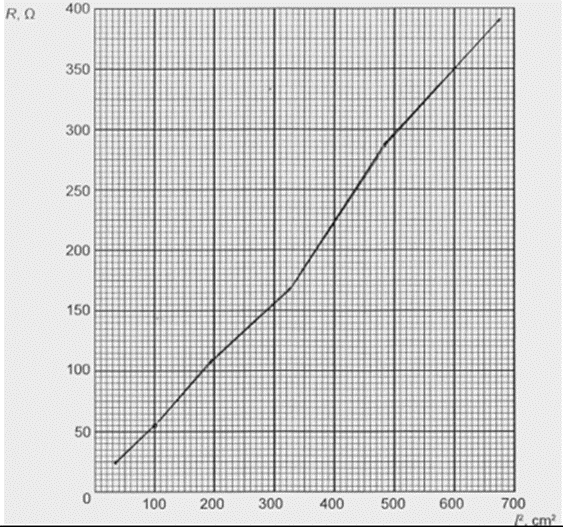
4. punkts
Uzdevuma izpilde eksāmenā – 69%.
Parādīts/paskaidrots, kā virziena koeficients rēķināts ("trīsstūrītis" nav ļoti maziņš) – 1 punkts.
Pareizi sarēķināts (der robežās 0,540 – 0,570, mērvienība var nebūt) – 1 punkts.
Zīmīgo ciparu skaitu nevērtē.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
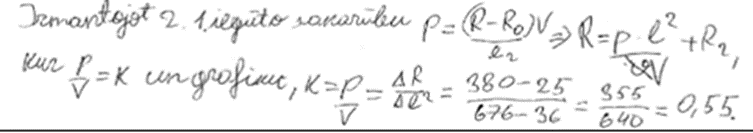
3. piemērs: risinājums novērtēts ar 1 punktu. Parādīts/paskaidrots, kā virziena koeficients rēķināts, nav sarēķināts.
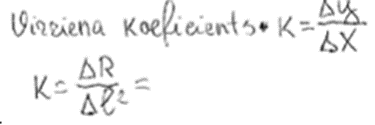
4. piemērs: risinājums novērtēts ar 0 punktu.
5. punkts
Uzdevuma izpilde eksāmenā – 48%.
Nosaukta/pieminēta īpatnējās pretestības saistība ar taisnes virziena koeficientu (ja paskaidrojumi sniegti punktos 1. vai 4., šo punktu te ieskaita) – 1 punkts.
Īpatnējā pretestība matemātiski izteikta ar virziena koeficientu vai uzrakstīts, ka jāzina tilpums, lai \(\rho\) sarēķinātu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 1 punktu. Ir doma par saistību ar virziena koeficientu, tikai nepareiza.
3. piemērs: risinājums novērtēts ar 0 punktu. Nav reālas saistības ar grafiku – datus var iegūt no tabulas.
6. punkts
Uzdevuma izpilde eksāmenā – 46%.
Uzraksta risinājuma gaitu: formula vai izteiksme uzrakstīta ar lielumu skaitliskajām vērtībām – 1 punkts
Iegūst skaitlisko vērtību robežās \(\mathrm{10,3\space\Omega\cdot cm}\) līdz \(\mathrm{10,6\space\Omega\cdot cm}\) – 1 punkts
Norāda mērvienību un zīmīgo ciparu skaits nepārsniedz piecus – 1 punkts.
Ja skolēns izvēlējies risinājuma veidu, kas nav aprakstīts kritērijos, vērtētājs patstāvīgi sadala risinājumu soļos, atbilstoši dotajam punktu skaitam.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 3 punktiem.
3. piemērs: risinājums novērtēts ar 2 punktiem. Pieņemts, ka \(R_0=0\space\Omega\), kas neatbilst grafikam.
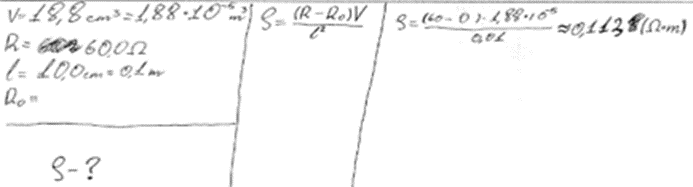
4. piemērs: risinājums novērtēts ar 1 punktu. Nepareiza mērvienība, nepareizi aprēķināts.
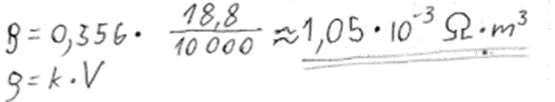
5. piemērs: risinājums novērtēts ar 0 punktu. Formula ir, bet nav saprasts, kādi lielumi tajā iekļauti.
7. punkts
Uzdevuma izpilde eksāmenā – 29%.
Uzdevumā jautāts, kādu informāciju var iegūt tieši IZMANTOJOT GRAFIKU. Tādēļ vērtē tikai tādu informāciju, kas iegūstama, izmantojot grafiku, citus spriedumus par eksperimenta iekārtu. Arī secinājums, ka grafika linearitāte liecina, ka īpatnējā pretestība ir konstants lielums, nav gluži secinājums par iekārtu. Tomēr, ja pieļauj, ka pētāmo materiālu var uztver kā iekārtas daļu, šādu atbildi šoreiz pieņemt.
Nosaukta \(R_0\) vai cita tālāk pamatota informācija – 1 punkts.
Paskaidrots, kā \(R_0\) iegūst (\(R_0\) vērtībai nav jābūt nosauktai) vai pamatojums citai no grafika iegūstamai informācijai – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
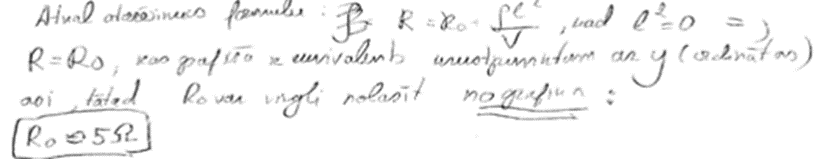
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 1 punktu. Par ideju.
4. piemērs: risinājums novērtēts ar 0 punktu.
