Attēlā redzams elementārdaļiņu standartmodelis.
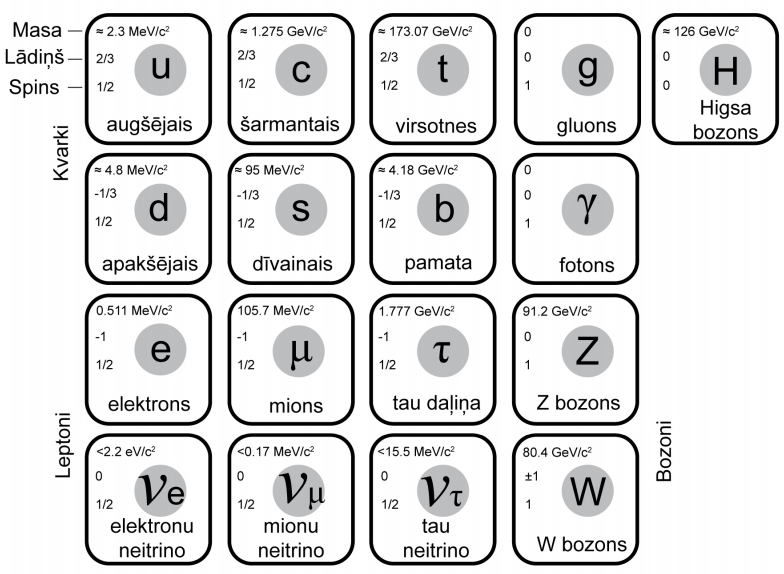
No kādiem trīs kvarkiem sastāv protons un neitrons?
Protons: ______________ ______________ ______________
Neitrons: ______________ ______________ ______________
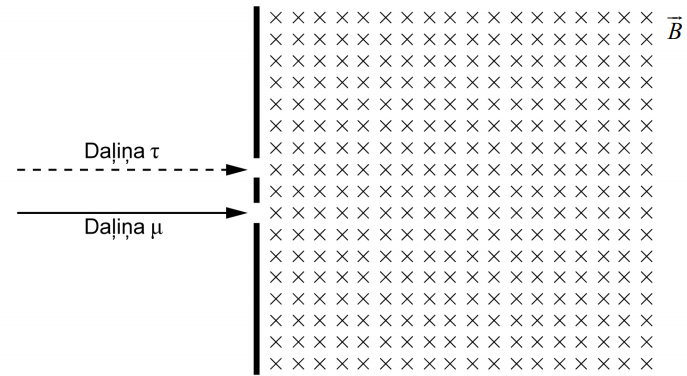
Daļiņas mioni \(\mu\) un tau \(\tau\) rodas daļiņu paātrinātājā un ar vienādu ātrumu ielido magnētiskajā laukā perpendikulāri indukcijas līnijām. Magnētiskā lauka indukcijas \(\overrightarrow{B}\) līnijas vērstas perpendikulāri zīmējuma plaknei prom no novērotāja. Attēlo zīmējumā \(\mu\) un \(\tau\) trajektorijas magnētiskajā laukā!
Pētot elementārdaļiņu īpašības, fiziķi Gells–Menns un Cveigs 1964. gadā formulēja hipotēzi, ka protons un neitrons sastāv no kvarkiem. Kvarku apzīmējumi: u (no angļu valodas “up” – augšējais), d (“down” – apakšējais). Pie tam d kvarkiem elektriskais lādiņš ir negatīvs \(-\frac{1}{3}e\), kur \(e\) – elektrona elektriskais lādiņš, bet u kvarkiem lādiņš ir pozitīvs \(+\frac{2}{3}e\). Pēc šī modeļa protons sastāv no diviem u kvarkiem un viena d kvarka, neitrons – no diviem d kvarkiem un viena u kvarka.
Protona (uud) lādiņš pēc moduļa ir vienāds ar elektrona lādiņu: \(+\frac{2}{3}e+\frac{2}{3}e+(-\frac{1}{3}e)=+1e\).
Neitronam (ddu) nav lādiņa: \(-\frac{1}{3}e-\frac{1}{3}e+\frac{2}{3}e=0\).
Piezīme: Uzdevumā nekas nebija jāskaidro, bija tikai jāpieraksta atbilde.
Atbilde:
Protons: uud jeb augšējais, augšējais un apakšējais kvarki.
Neitrons: ddu jeb augšējais, apakšējais un apakšējais kvarki.
Lādētas daļiņas kustības trajektorija ir atkarīga no magnētiskā lauka indukcijas \(\overrightarrow{B}\) un lādētās daļiņas parametriem – elektriskā lādiņa \(q\) un kustības ātruma \(\overrightarrow{v}\). Tā kā lādētās daļiņas ielido magnētiskajā laukā \(90^0\) lielā leņķī attiecībā pret indukcijas līnijām, daļiņu kustības trajektorijas magnētiskajā laukā ir riņķa līnijas.
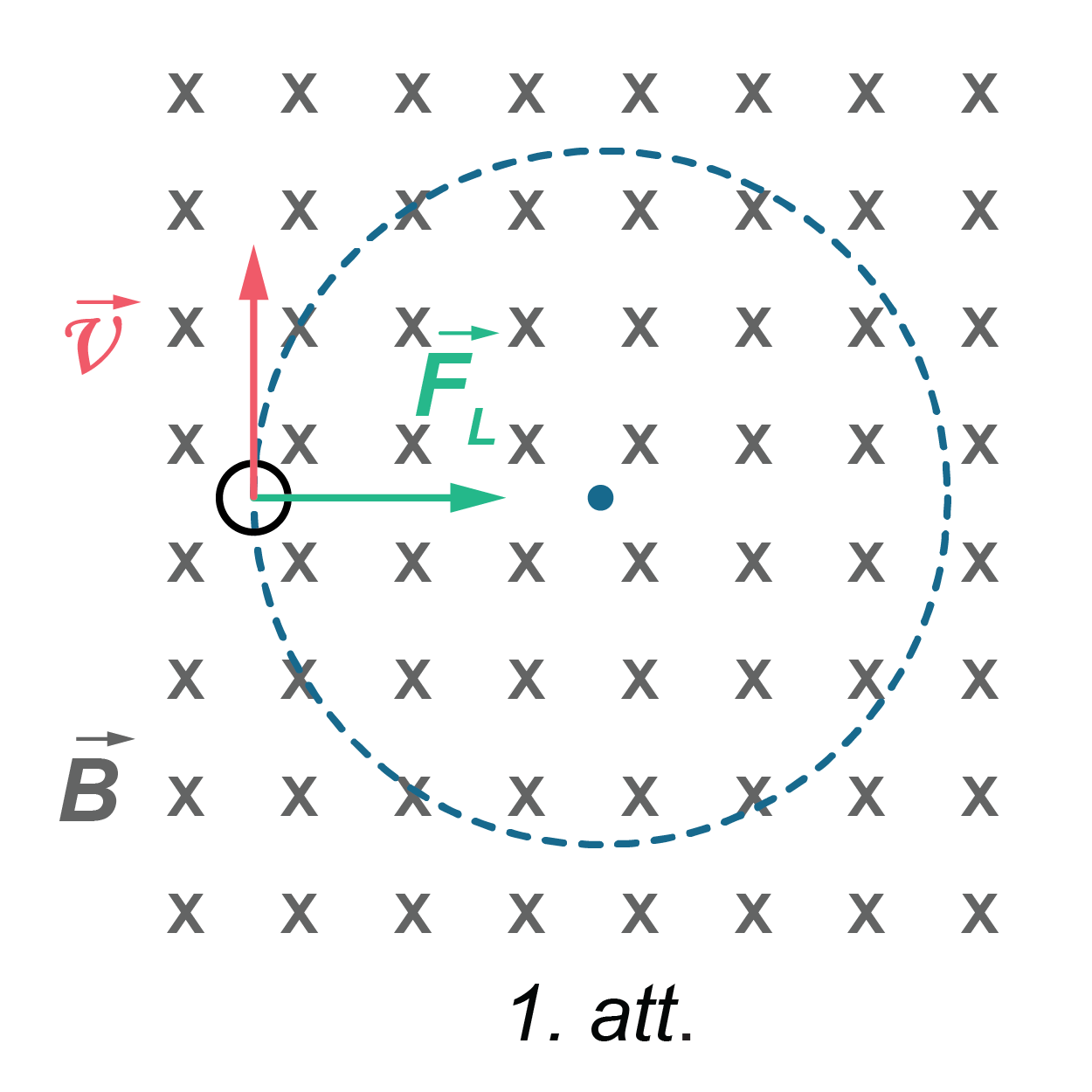
Uz daļiņu, kas ielido magnētiskajā laukā, darbojas Lorenca spēks \(F_\mathrm{L}=qvB\), kas piešķir daļiņai centrtieces paātrinājumu \(a_\mathrm{c}=\frac{v^2}{R}\) (1. att.), kur \(R\) – kustības trajektorijas (riņķa līnijas) rādiuss.
Saskaņā ar II Ņūtona likumu:
\(F_\mathrm{L}=ma_\mathrm{c}\)
\(qvB=m\frac{v^2}{R}\).
No vienādojuma izsakot daļiņas trajektorijas liekuma rādiusu, iegūst \(R=\frac{mv}{qB}\).
No izteiksmes redzams, ka daļiņas kustības trajektorijas liekuma rādiuss ir atkarīgs no daļiņas masas \(m\), kustības ātruma \(v\), daļiņas elektriskā lādiņa \(q\) un magnētiskā lauka indukcijas \(B\).
Atbilstoši uzdevuma nosacījumiem, mionam \(\mu\) un daļiņai \(\tau\) (tau) piemīt vienāds elektriskais lādiņš \(q\) un vienāds kustības ātrums \(v\). Daļiņu lādiņš ir negatīvs un tās ielido vienā un tajā pašā magnētiskajā laukā. Atšķiras vienīgi daļiņu masa – jo lielāka masa, jo lielāks trajektorijas liekuma rādiuss. No uzdevumā piedāvātā standartmodeļa attēla nosaka miona masu – 105,7 MeV/c2 un tau daļiņas masu – 1,777 GeV/c2 (daļiņu masas var salīdzināt pēc Einšteina formulas \(E=mc^2 \space \implies \space m=\frac{E}{c^2}\), kur \(E\) – daļiņas enerģija, \(m\) – daļiņas masa, \(c\) – elektromagnētisko viļņu izplatīšanās ātrums vakuumā)
Lai salīdzinātu daļiņu masas, jāsaskaņo mērvienības. 1 GeV = 1000 MeV. Tātad, tau daļiņas masa ir 1777 MeV/c2, kas ir aptuveni 17 reizes lielāka, nekā miona masa. Secinājums – tau daļiņas trajektorijas liekuma rādiuss \(R=\frac{mv}{qB}\) magnētiskajā laukā ir ap 17 reizēm lielāks, nekā miona trajektorijas liekuma rādiuss. Masu ir iespējams novērtēt nerēķinot – jo lielāka ir daļiņas enerģija, jo lielāka ir tās masa. Daļiņas tau un miona enerģiju nolasa no uzdevumā dotā standartmodeļa attēla.
Daļiņas kustības virzienu nosaka pēc tā, kādā virzienā darbojas Lorenca spēks. To var veikt, piemēram, pēc kreisās rokas paņēmiena. Uzdevumā daļiņas magnētiskajā laukā sāk kustību uz leju (2. att.).
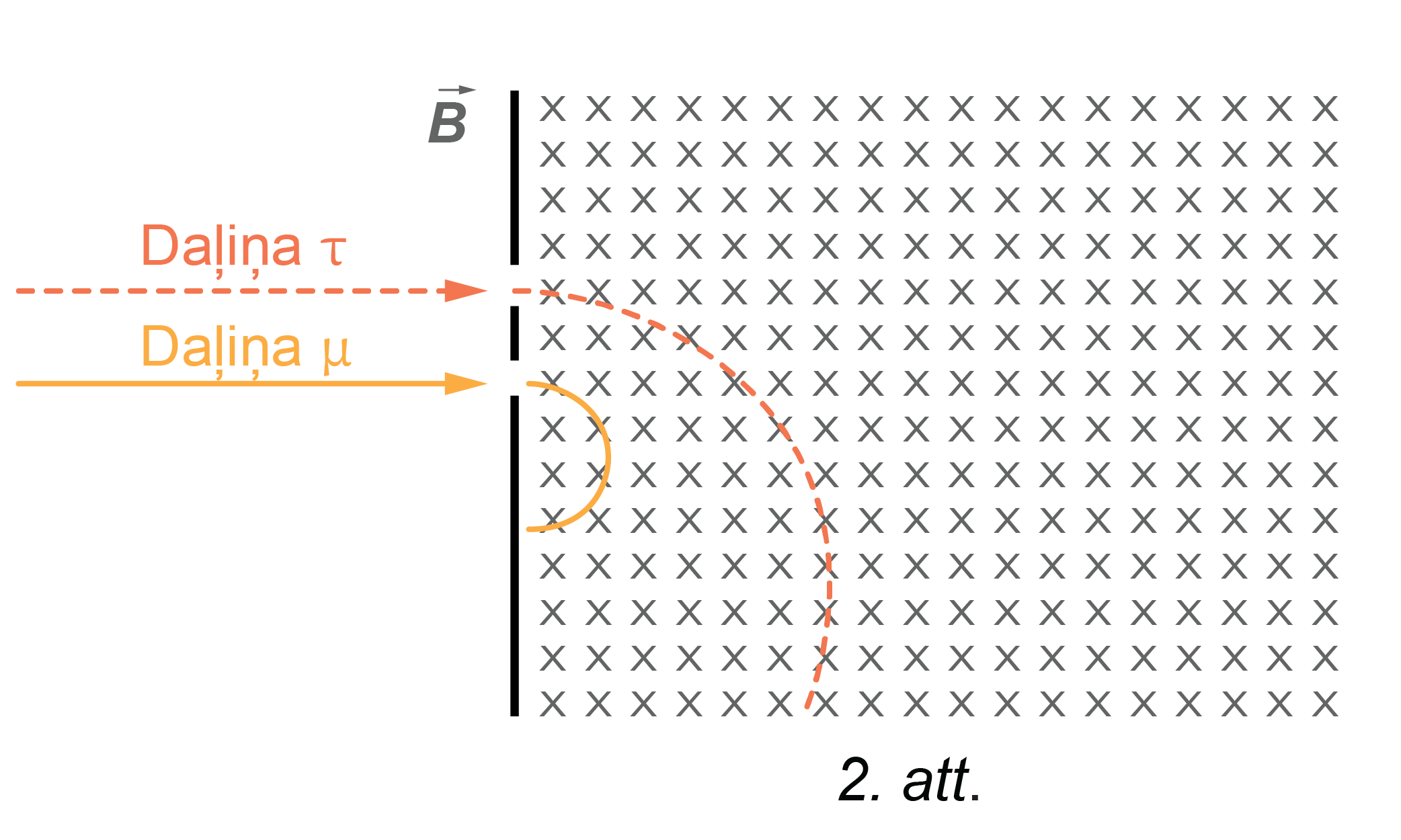
Piezīme 1.: Zīmējums nav veikts mērogā.
Piezīme 2.: Arī šajā punktā eksāmenā netika prasīts skaidrojums, bija jāiezīmē katras daļiņas kustības trajektorija.
Vērtēšanas kritēriji
Zina, pēc kādām pazīmēm ir klasificētas elementārdaļiņas standartmodelī – 1 punkts par katru daļiņu.
Attēlo zīmējumā daļiņu trajektorijas kā riņķa līnijas, kas magnētiskajā laukā noliecās "uz leju" – 1 punkts.
Attēlo zīmējumā daļiņu trajektorijas ar dažādiem rādiusiem (tau daļiņas trajektorijas rādiuss ir lielāks nekā miona) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem.
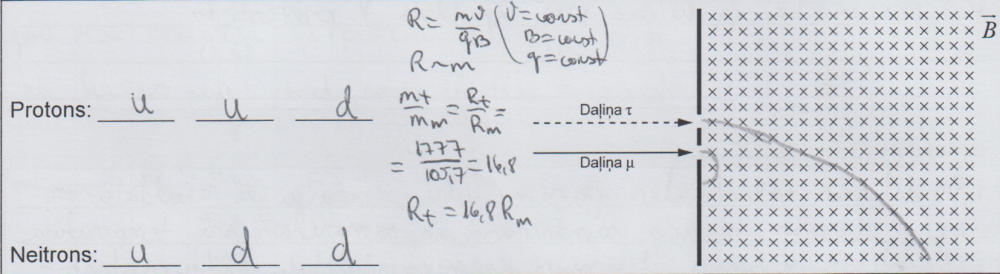
2. piemērs: risinājums novērtēts ar 4 punktiem.

3. piemērs: risinājums novērtēts ar 3 punktiem (virzieni nav pareizi).

4. piemērs: risinājums novērtēts ar 3 punktiem (neattēlo zīmējumā, ka tau daļiņas trajektorijas rādiuss ir lielāks nekā miona).

5. piemērs: risinājums novērtēts ar 1 punktu (tikai par daļiņu trajektoriju dažādu rādiusu attēlošanu).
