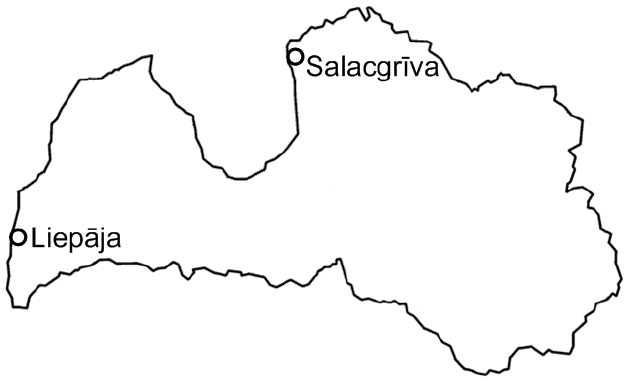
Festivālā Positivus, kas katru gadu notiek Salacgrīvā, klausītājs vienā no koncertiem atrodas \(300\space\mathrm m\) attālumā no skatuves. Festivālu translē arī pa radio. Cits klausītājs Liepājā koncertu klausās pa radio, un skaņa to sasniedz nedaudz ātrāk nekā klausītāju koncertā.
1. Izskaidro, kāpēc ir iespējama situācija, ka klausītājs Liepājā dažkārt dzird koncertu pirms klausītāja festivālā uz vietas!
2. Koncertu pa radio klausās arī divās automašīnās – A un B. Koncertu pārraida, izmantojot divas frekvences – frekvenci \(1152\space\mathrm{kHz}\) ar amplitūdas modulāciju (AM) un frekvenci \(102,5\space\mathrm{MHz}\) ar frekvences modulāciju (FM). Automobilī A radio klausās AM diapazonā, bet automobilī B – FM diapazonā. Abi automobiļi iebrauc ielejā, ko norobežo kalnains apvidus. Izskaidro, kāpēc automobilī A koncerts ir dzirdams visu laiku, bet automobilī B signāls no raidītāja nepienāk un koncerts nav dzirdams!
1. Līdz klausītājam uz vietas Salacgrīvā skaņa nonāk, izplatoties gaisā ar ātrumu \(330\space\mathrm{m/s}\). Pieņemsim, ka klausītājs atrodas \(330\space\mathrm{m}\) attālumā no skatuves. Zinot sakarību starp ātrumu, veikto ceļu un laiku \(v=\frac{s}{t}\), var aprēķināt laiku, kādā skaņa nokļūst līdz klausītājam: \(t_1=\frac{s_1}{v_1}=\frac{330}{330}=1\space\mathrm s\).
Līdz klausītājam Liepājā koncerts tiek raidīts ar radiovilņu palīdzību. Radioviļņi (kā jebkuri elektromagnētiskie viļņi) gaisā izplatās ar gaismas ātrumu \(3\cdot10^5\space\mathrm {km/s}\). Ja pieņem, ka Liepāja no Salacgrīvas atrodas \(270\space\mathrm{km}\) lielā attālumā, tad radiosignāls Liepājā nokļūst laikā \(t_2=\frac{s_2}{v_2}=\frac{270}{3\cdot10^5}\approx 0,9\cdot10^{-3}\space\mathrm s\), kas ir ievērojami mazāk, nekā \(1\space\mathrm s\)! Tāpēc ir iespējama situācija, ka klausītājs Liepājā dažkārt dzird koncertu pirms klausītāja festivālā uz vietas.
2. Difrakcija ir viļņu (elektromagnētisko, mehānisko u.c.) apliekšanās ap dažādām nehomogenitātēm (šķēršļiem) vidē, kas atrodas to izplatīšanās ceļā. Difrakcija ir novērojama, ja viļņa garums ir salīdzināms ar šķēršļa izmēru.
Viļņa garumu \(\lambda\) nosaka pēc formulas \(\lambda=cT\), kur \(c\) – elektromagnētiskā viļņa izplatīšanās ātrums gaisā, \(T\) – viļņa periods. Viļņa periods \(T\) un viļņa frekvence \(f\) ir savstarpēji apgriezti lielumi \(T=\frac{1}{f}\). Tādēļ viļņa garumu \(\lambda\) nosaka arī pēc formulas \(\lambda=\frac{c}{f}\).
AM diapazons: viļņa garums \(\lambda_{\mathrm{AM}}=\frac{c}{f_{\mathrm{AM}}}=\frac{3\cdot10^8}{1152\cdot10^3}\approx260\space\mathrm m\).
FM diapazons: viļņa garums \(\lambda_{\mathrm{FM}}=\frac{c}{f_{\mathrm{FM}}}=\frac{3\cdot10^8}{102,5\cdot10^6}\approx2,9\space\mathrm m\).
Skaidrs, ka viļņi, kuru garums ir \(260\space\mathrm m\), var apiet virsmas reljefu. Savukārt viļņi, kuru garums ir \(2,9\space\mathrm m\), izplatās praktiski tikai taisnā virzienā. Tādēļ AM stacija aiz kalniem ir dzirdama, bet FM stacija – nē.
Vērtēšanas kritēriji
1. Salīdzina signāla izplatīšanās laiku – 1 punkts
2. Aprēķina viļņa garumu – 1 punkts. Secina par viļņu izplatīšanos – 1 punkts.