Velosipēdista kustību pa horizontālu ceļa posmu raksturo koordinātas vienādojums \(x=4+t^2\).
Fizikālie lielumi vienādojumā ir norādīti SI vienībās.
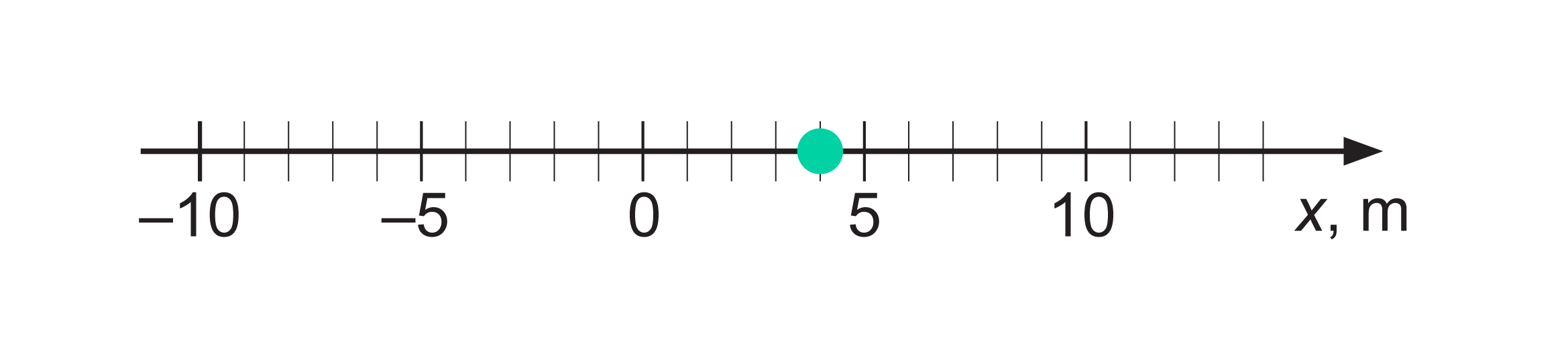
1. Uz koordinātu ass atzīmē punktu, kas atbilst riteņbraucēja pozīcijai sākotnējā laika momentā! (1 punkts)
2. No koordinātas vienādojuma nosaki velosipēdista sākotnējo ātrumu \(v_0\) un paātrinājumu \(a\)! (2 punkti)
3. Velosipēdista ātrums trijās sekundēs izmainās par \(6~\mathrm{m/s}\). Aprēķini velosipēdista impulsa izmaiņu, ja zināms, ka viņa masa ir \(60~\mathrm{kg}\)! (2 punkti)
4. Aprēķini velosipēdista vidējo ātrumu pirmajās astoņās sekundēs! (2 punkti)
5. Grafikos I un II attēlota paātrinājuma un ātruma atkarība no laika.
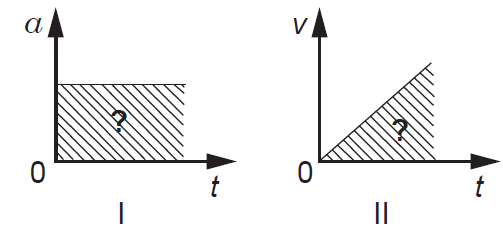
Kurus fizikālos lielumus var noteikt, aprēķinot iesvītrotā laukuma skaitlisko vērtību grafikā I un grafikā II? (2 punkti)
6. Vējš pūš velosipēdista kustības virzienā viņam tieši mugurā ar ātrumu, kas lielāks nekā velosipēdista ātrums. Pamato, kāpēc vēja ātrums ar velosipēdistu saistītajā atskaites sistēmā ir mazāks nekā ar zemi saistītajā atskaites sistēmā! (1 punkts)
1. Jāzina vai jāatrod datu bukletā ķermeņa kustības vienādojums vienmērīgi paātrinātas kustības gadījumā:
\(x=x_0+v_0t+\frac{at^2}{2}\). Konkrētajā gadījumā \(x=4+t^2\) (\(x=4+0\cdot t+\frac{2t^2}{2}\)).
Tātad sākuma koordināta ir \(x_0=4\space\mathrm{m}\).
Atbilde:
2. Jāzina vai jāatrod datu bukletā ķermeņa kustības vienādojums vienmērīgi paātrinātas kustības gadījumā:
\(x=x_0+v_0t+\frac{at^2}{2}\). Konkrētajā gadījumā \(x=4+t^2\) (\(x=4+0\cdot t+\frac{2t^2}{2}\)). Tātad: \(v_0=0\space\mathrm{m/s}\); \(a=2\space\mathrm{m/s^2}\)
Atbilde: \(v_0=0\space\mathrm{m/s}\); \(a=2\space\mathrm{m/s^2}\)
3. Jāzina vai jāatrod datu bukletā sakarību ķermeņa impulsa aprēķināšanai \(p=mv\). Konkrētajā situācijā ķermeņa masa nemainās, tātad impulsa izmaiņa \(\Delta p=m\Delta v=60\cdot6=360\space\mathrm{\frac{{kg\cdot m}}{s}}\). Šādi risinot, fakts, ka ātruma izmaiņa notika trijās sekundēs, nav jāizmanto.
Alternatīvs risinājuma variants: var izmantot iepriekš iegūto paātrinājuma vērtību \(a=2\space\mathrm{m/s^2}\), datu bukletā atrodamo sakarību, kas saista spēku ar ķermeņa impulsa izmaiņu: \(F=\frac{\Delta p}{\Delta t}\) un Otro Ņutona likumu \(F=ma\), lai noteiktu spēku, kas ķermenim piešķir paātrinājumu \(a\). Tad \(\Delta p=F\Delta t=ma\Delta t=60\cdot2\cdot3=360\space\mathrm{\frac{kg\cdot m}{s}}\).
Atbilde: impulsa izmaiņa \(\Delta p=360\space\mathrm{\frac{{kg\cdot m}}{s}}\).
4. Jāzina, ka vidējo ātrumu aprēķina, dalot visu kustības laikā veikto ceļu ar kopējo kustības laiku: \(v_\mathrm{vid}=\frac{l}{t}\).
Tātad vispirms jānosaka pirmajās astoņās sekundēs veiktais ceļš. Var izmantot kustības vienādojumu: \(x=4+t^2=4+8^2=68\space\mathrm{m}\) velosipēdista koordināta pēc 8 sekundēm. Taisnlīnijas kustībā veiktais ceļš ir vienāds ar pārvietojumu
\(l=s=x-x_0=68-4=64\space\mathrm{m}\).
Var aprēķināt 8 sekundēs sasniegto ātrumu \(v=at=2\cdot8=16\space\mathrm{m/s}\) un tad veikto ceļu (pārvietojumu), izmantojot formulu lapā atrodamo sakarību \(v^2-v_0^2=2as\):
\(s=\frac{v^2-v_0^2}{2a}=\frac{16^2-0^2}{2\cdot2}=64\space\mathrm{m}\)
Zinot veikto ceļu, var aprēkināt vidējo ātrumu: \(v_\mathrm{vid}=\frac{l}{t}=\frac{64}{8}=8\space\mathrm{m/s}\).
Atbilde: \(v_\mathrm{vid}=8\space\mathrm{m/s}\).
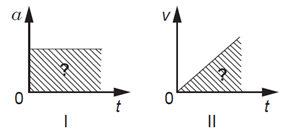5. Jāzina, ka ātruma izmaiņa vienāda ar laukumu zem paātrinājuma grafika atkarībā no laika (\(v=at\) – iesvītrotā taisnstūra laukums), bet veiktais ceļš vienāds ar laukumu zem ātruma grafika atkarībā no laika (šajā gadījumā \(l=v_\mathrm{vid}t=\frac{v_{\mathrm{max}}t}{2}\) iesvītrotā trijstūra laukums).
Atbilde: I – ceļš; II – ātrums.
6. Tā kā vējš pūš velosipēda kustības virzienā, vēja ātrums attiecībā pret velosipēdu \(v_\mathrm{vv}\) ir mazāks kā vēja ātrums attiecībā pret zemi \(v_\mathrm{vz}\) – tieši par velosipēda kustības ātrumu attiecībā pret zemi \(v_\mathrm{v}\).
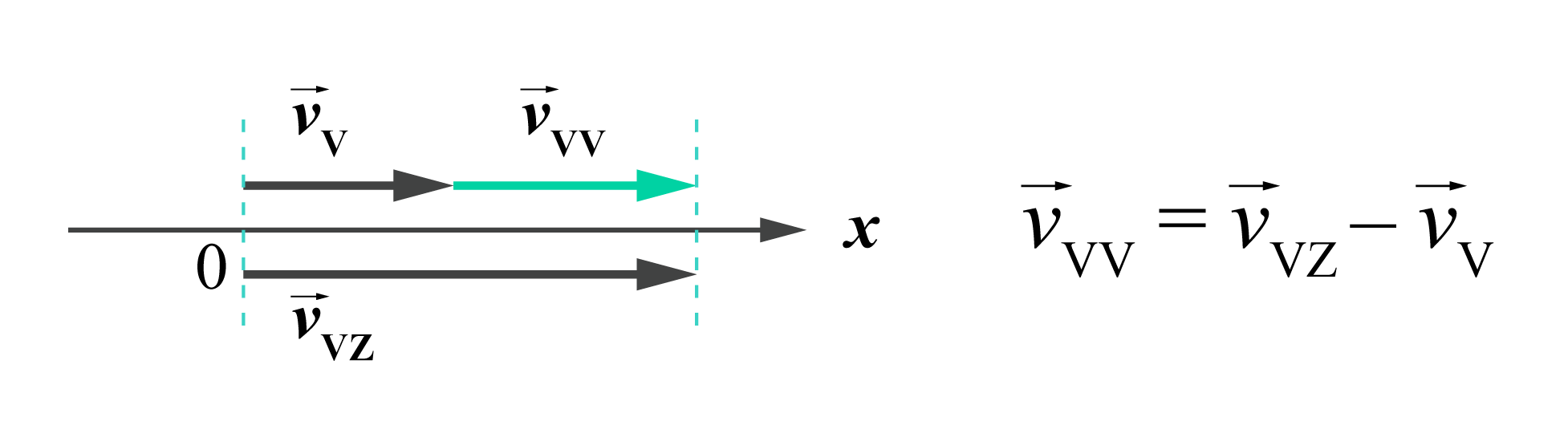
Atbilde: tā kā attiecībā pret zemi vējš un velosipēds kustas vienā virzienā, tad attiecībā pret velosipēdu vēja ātrums ir mazāks, nekā attiecībā pret zemi: \(v_\mathrm{vv}=v_\mathrm{vz}-v_\mathrm{v}\).
1. Vērtēšanas kritēriji
Nosaka riteņbraucēja sākuma pozīciju un atzīmē uz koordinātu ass – 1 punkts.
Atbilde \(x_0=4\space\mathrm{m}\) tieši nolasāma koordinātas vienādojumā, ja punkts uz koordinātu ass atzīmēts pareizi, atbildes pamatojums nav nepieciešams. Par nekorektu pamatojumu punktu neatņem.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
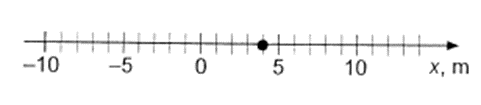
2. piemērs: risinājums novērtēts ar 0 punktu.
2. Vērtēšanas kritēriji
- No koordinātas vienādojumu nosaka sākotnējo ātrumu \(v_0\) – 1 punkts
- No koordinātas vienādojumu nosaka paātrinājumu \(a\) – 1 punkts
Kustības vienādojums dots uzdevuma tekstā, atbildes pamatojums nav nepeciešams. Ja norādīta mērvienība paātrinājumam, sākuma ātruma mērvienība var nebūt norādīta.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
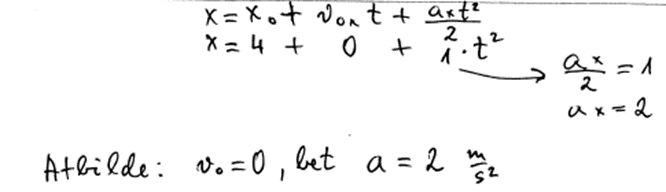
2. piemērs: risinājums novērtēts ar 2 punktiem.
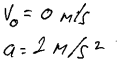
3. piemērs: risinājums novērtēts ar 1 punktu. Pareizi noteikts tikai viens prasītais lielums.
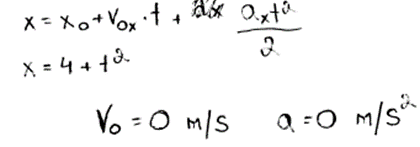
4. piemērs: risinājums novērtēts ar 0 punktu.
3. Vērtēšanas kritēriji
- Uzraksta risinājuma gaitu impulsa izmaiņas aprēķināšanai: formula un/vai formulās ievietoti skaitļi – 1 punkts.
- Skaitliski aprēķina impulsa izmaiņu, uzraksta mērvienību – 1 punkts.
Ja aprēķināts impulss \(p=m\ v=60\cdot6=360\space\mathrm{\frac{{kg\cdot m}}{s}}\), nevis impulsa izmaiņa – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
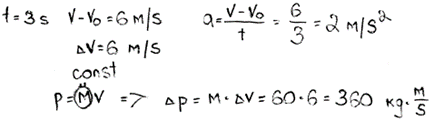
2. piemērs: risinājums novērtēts ar 1 punktu. Aprēķināts impulss, nevis impulsa izmaiņa.
3. piemērs: risinājums novērtēts ar 0 punktu.
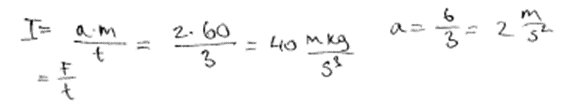
4. Vērtēšanas kritēriji
- Uzraksta risinājuma gaitu vidējā ātruma aprēķināšanai – 1 punkts
- Skaitliski aprēķina vidējo ātrumu, izsakot veikto ceļu no kustības vienādojuma vai kā citādi – 1 punkts
Ja uzrakstīts, ka kustība ir vienmērīgi paātrināta, vidējo ātrumu var rēķināt: \(v_\mathrm{vid}=\frac{v-v_0}{2}\). Pieļaujamas nepilnības pierakstā, aprēķinot veikto ceļu.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
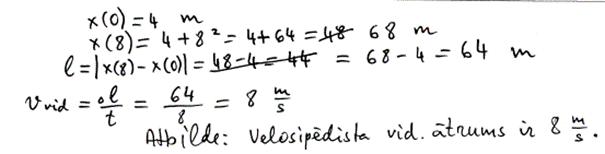
2. piemērs: risinājums novērtēts ar 1 punktu. Punkts piešķirts par pareizi uzrakstīto formulu vidējā ātruma aprēķināšanai.
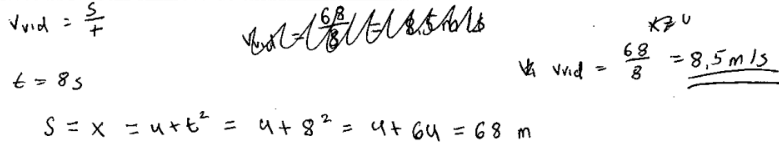
3. piemērs: risinājums novērtēts ar 0 punktu.
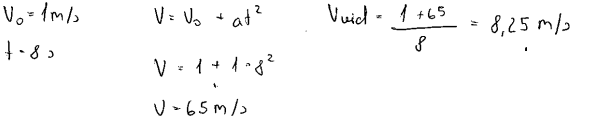
5. Vērtēšanas kritēriji
- Pareiza atbilde par grafiku I: ātrums (der arī atbildes "beigu ātrums", "momentānais ātrums", "ātruma izmaiņa") – 1 punkts. Par atbildi "vidējais ātrums" punktu neieskaita.
- Pareiza atbilde par grafiku II: ceļš – 1 punkts
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
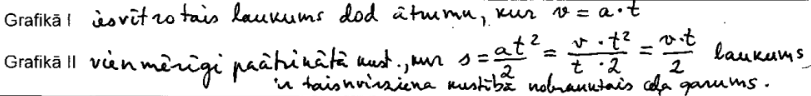
2. piemērs: risinājums novērtēts ar 2 punktiem.
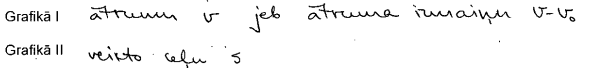
3. piemērs: risinājums novērtēts ar 1 punktu. Pareizi sniegta atbilde tikai par pirmo grafiku.
4. piemērs: risinājums novērtēts ar 0 punktu.
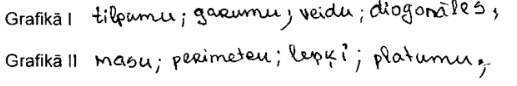
6. Vērtēšanas kritēriji
Skaidro, izmantojot ideju par ātruma noteikšanu kustīgā atskaites sistēmā (ātrumu vektoriāla saskaitīšana) un faktu, ka vējš un velosipēds kustas vienā virzienā – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
2. piemērs: risinājums novērtēts ar 1 punktu.
3. piemērs: risinājums novērtēts ar 0 punktu.
