Automašīnas ātruma projekcijas \(v_{\mathrm x}\) izmaiņa atkarībā no laika \(t\) dota attēlā.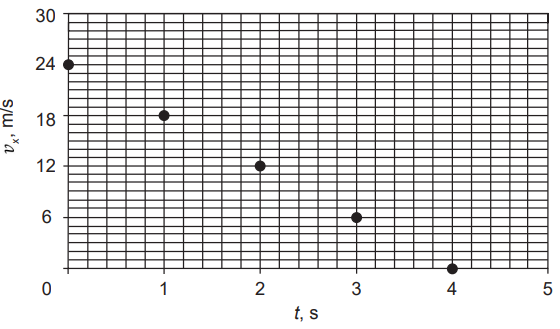
Uzraksti automašīnas ātruma projekcijas vienādojumu gan vispārīgā veidā, gan dotajam gadījumam! Parādi risinājuma gaitu!
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Ātruma projekcijas \(v_\mathrm x\) vienādojumu sastāda no paātrinājuma projekcijas \(a_\mathrm x\) formulas: \(a_\mathrm x=\frac{v_\mathrm x-v_\mathrm{0x}}{t}\), kur \(v_\mathrm {0x}\) – sākuma ātruma projekcija, \(t\) – kustības laiks. No vienādojuma izsaka ātruma projekciju un iegūst ātruma projekcijas vienādojumu vispārīgā veidā \(v_\mathrm x=v_\mathrm {0x}+a_\mathrm x t\).
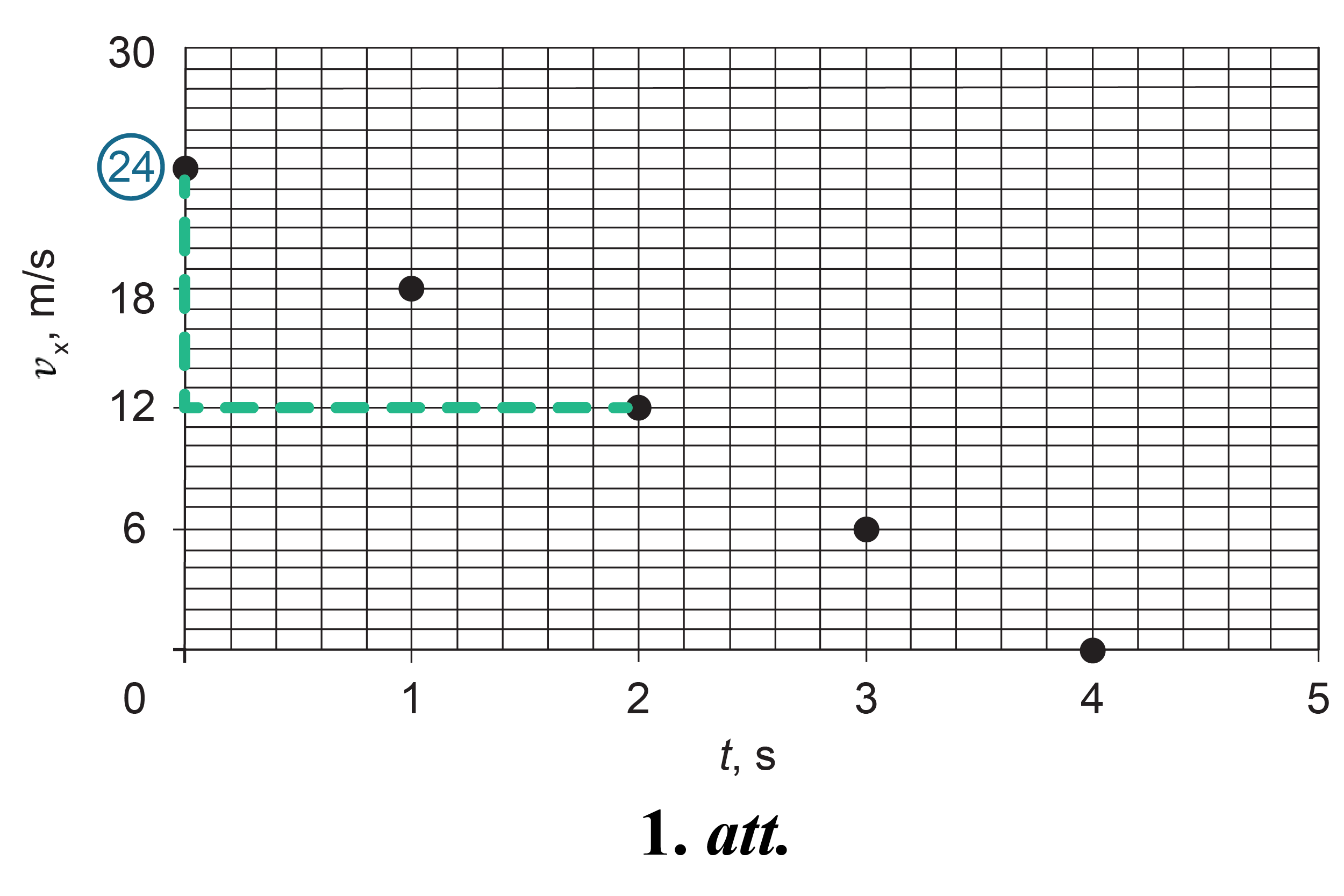
Sākuma ātruma projekcijas vērtību \(v_\mathrm{0x}\) nolasa no grafika (1. att.). Uzdevumā \(v_\mathrm{0x}=24\space\mathrm{m/s}\). Sākuma ātruma projekcija ir pozitīva, tādēļ automašīna kustas X ass virzienā (2. att.).
Kustības laikā automašīna bremzē, tādēļ ātruma modulis samazinās. Tādēļ paātrinājuma vektors vērsts pretēji sākuma ātruma vektoram jeb pretēji X ass virzienam (2. att.). Tādēļ paātrinājuma projekcija ir negatīva, \(a_\mathrm x <0\).
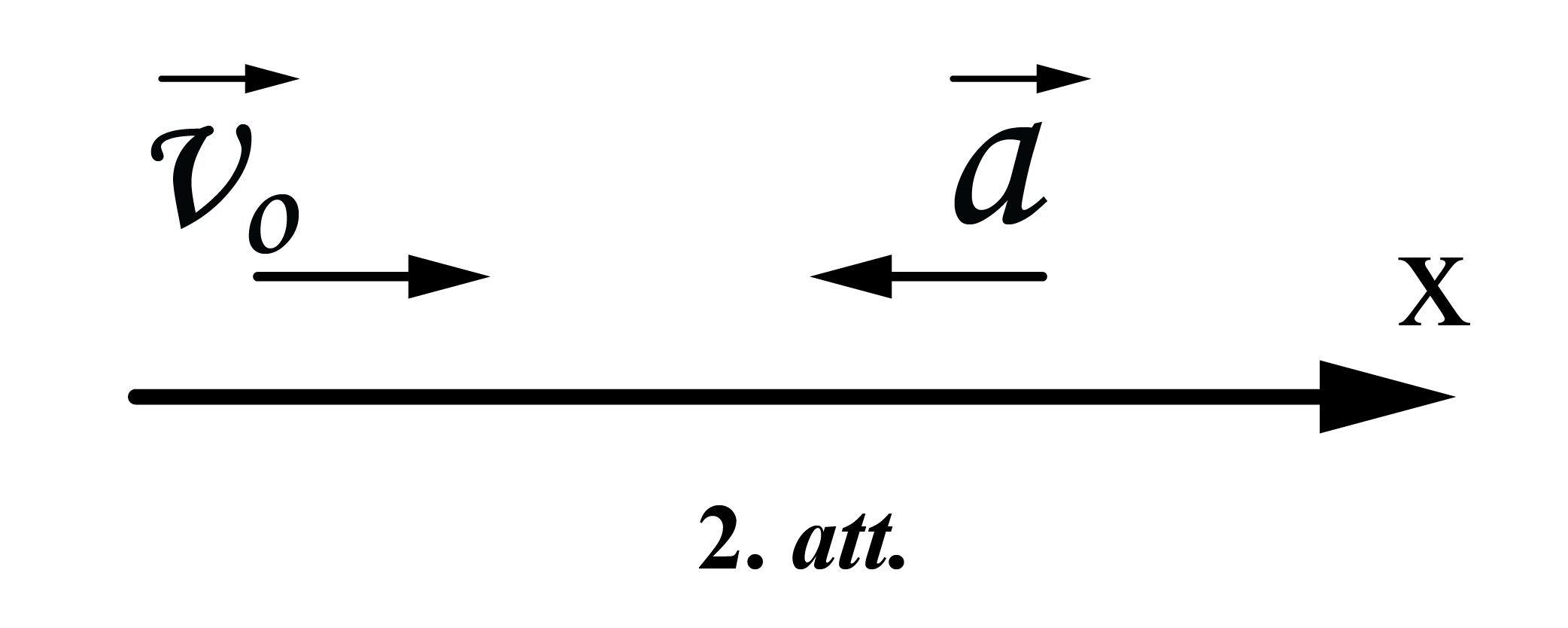
Paātrinājuma moduli nolasa, izmantojot paātrinājuma definīciju: paātrinājums ir skaitliski vienāds ar ātruma izmaiņu laika vienībā. Zīmējumā (1.att.) ātruma modulis samazinās divu sekunžu laikā par \(24-12=12\space\mathrm{m/s}\). Tadēļ paātrinājuma modulis ir vienāds \(\frac{12}{2}=6\space\mathrm{m/s^2}\). Paātrinājuma projekcija \(a_\mathrm x=-6\space\mathrm{m/s^2}\).
Ātruma projekcijas vienādojums: \(v_\mathrm x=24-6t\). Laiks mainās intervālā no \(0\) līdz \(4\space\mathrm s\).
Piezīme: paātrinājuma projekciju var noteikt formāli pēc formulas \(a_\mathrm x=\frac{v_\mathrm x-v_\mathrm{0x}}{t}\). No grafika (1. att.) nolasa lielumu skaitliskās vērtības. Piemēram: \(v_\mathrm {0x}=24\space\mathrm{m/s}\); \(v_\mathrm {x}=0\); \(t=4\space\mathrm s\). Tad \(a_\mathrm {x}=\frac{0-24}{4}=-6\space\mathrm{m/s^2}\).
Uzdevuma izpilde eksāmenā - 51,2%.
Vērtēšanas kritēriji
Uzraksta taisnes vienādojumu vispārīgā formā – 1 punkts.
Nolasa no grafika atbilstošās vērtības un aprēķina paātrinājumu – 1 punkts.
Uzraksta ātruma projekcijas vienādojumu – 1 punkts.