2012. gadā pasaules rekordu uzstādīja Jelgavā ražotais mini bezpilota lidaparāts (drons) „Penguin B”, lidojumā pavadot 54 stundas un 27 minūtes (avots: Neatkarīgā rīta avīze).
1. Nosaki lidaparāta veikto ceļu šajā laikā, ja tas pārvietojas ar vidējo ātrumu 70 km/h.
2. Uzzīmē spēkus, kas darbojas uz lidaparātu tā vienmērīgas horizontālas kustības laikā! Pieņem, ka spēki pielikti masas centrā O! Spēku mērogu vari neievērot! Pieraksti šo spēku nosaukumus!

3. Cik liels smaguma spēks darbojas uz lidaparātu, ja tā masa kopā ar kravu ir 17 kg?
4. Vai šo lidaparātu var izmantot uz Mēness? Pamato atbildi!
1.
Bezpilota lidaparāta veikto ceļu \(s\) nosaka pēc formulas \(s=v_{\mathrm{vid}}t\), kur \(v_\mathrm{vid}\)– lidaparāta lidojuma vidējais ātrums, \(t\) – lidojuma laiks.
Aprēķini:
doto lidojuma laiku pārveidojot stundās, iegūst \(\mathrm{54 \space h \space 27 \space min = \mathrm{54\space h+\frac{27}{60}\space h=54,45 \space h}}\).
\(s=v_\mathrm{vid}t=70\mathrm{km/h}\cdot54,45\space\mathrm{h}=3811,5\space\mathrm{km}\approx3,8\cdot10^3\space\mathrm{km}\)
Piezīme: aprēķinos var izteikt lidojuma laiku un ātrumu SI pamatvienībās.
Tad lidojuma laiks \(\mathrm{54\space h \space 27\space min = 54·3600 + 27·60 = 194400 + 1620 =196020 \space s ≈ 1,96·10^5\space s}\).
Lidojuma vidējais ātrums \(\mathrm{70 \space km/h=\frac{70 \cdot 1000 \space m}{3600\space s}≈19,4 \space m/s}\).
\(s=v_\mathrm{vid}t=19,4\space\mathrm{m/s}\cdot 1,96\cdot 10^5\space\mathrm{s}\approx3,8\cdot10^6\space\mathrm{m}=3,8\cdot10^3\space\mathrm{km}\)
Atbilde:
lidaparāta veiktais ceļš \(3,8\cdot10^6\space\mathrm{m}=3,8\cdot10^3\space\mathrm{km}\).
2.
Lidaparāts kustas vienmērīgi horizontālā virzienā. Tātad, ātrums nemainās laikā un, saskaņā ar I Ņūtona likumu, kopspēks, kas darbojas uz dronu, ir vienāds ar nulli. Uz lidaparātu darbojas četri spēki (skatīt attēlu). Vertikāli uz leju – smaguma spēks \(\overrightarrow{F_\mathrm{sm}}\), vertikāli uz augšu – spārnu cēlējspēks \(\overrightarrow{F_\mathrm{cel}}\). Kustības virzienā – dzinēja vilcējspēks \(\overrightarrow{F_\mathrm{vilc}}\), pretēji kustības virzienam – gaisa pretestības spēks \(\overrightarrow{F_\mathrm{pret}}\).
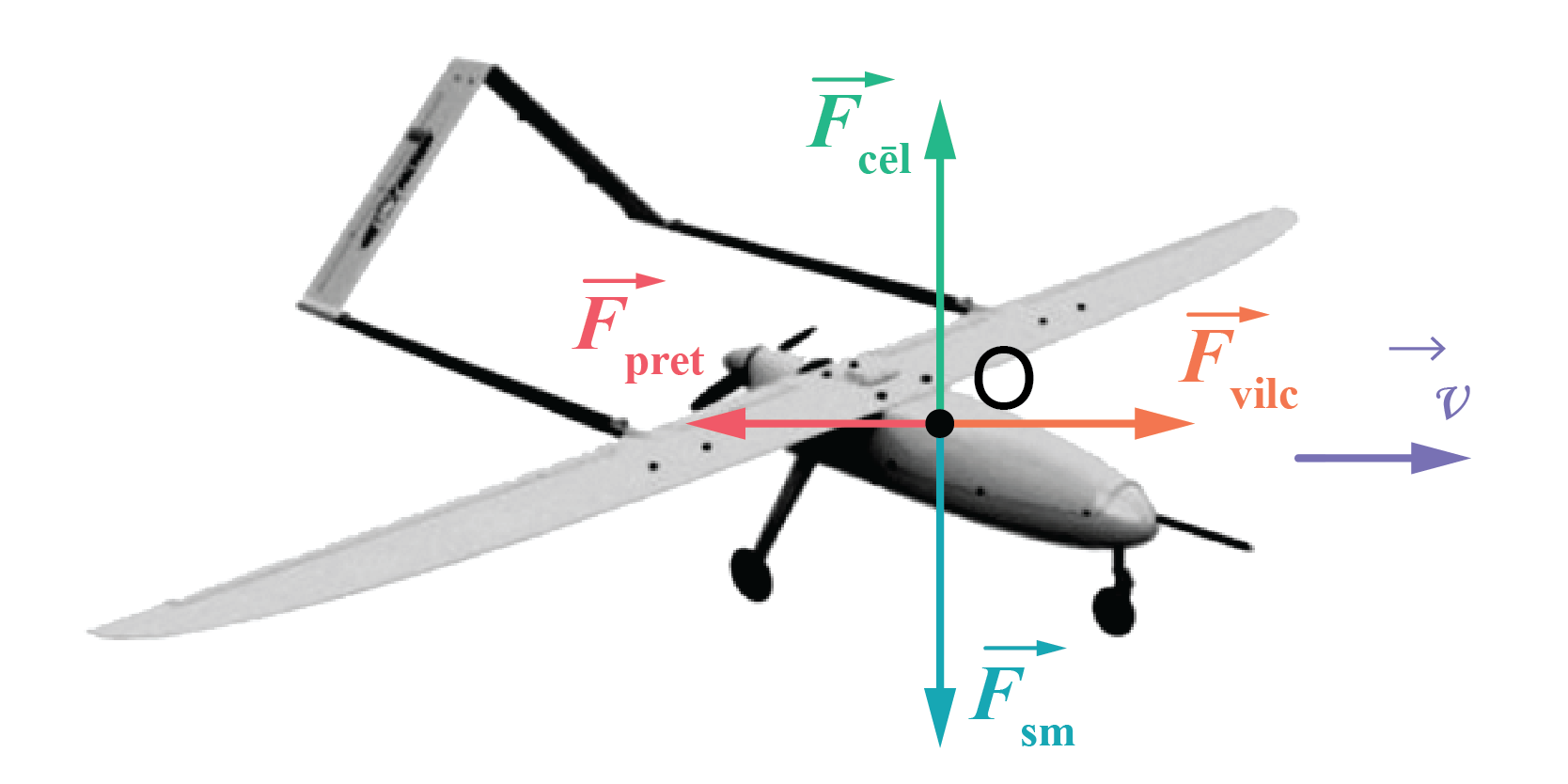
Pretēji vērstie spēki pēc moduļiem ir vienādi: \({F_\mathrm{sm}}={F_\mathrm{cel}}\) un \({F_\mathrm{vilc}}={F_\mathrm{pret}}\).
Piezīmes:
a) Arhimēda spēks ir ļoti mazs, salīdzinājumā ar citiem spēkiem – attēlot to nav nepieciešams;
b) spēkiem var būt arī citi nosaukumi, piemēram, nevis smaguma spēks, bet gravitācijas spēks.
3.
Ķermeņa smaguma spēku \(F_\mathrm{sm}\) nosaka pēc formulas \(F_\mathrm{sm}=mg\), kur \(m\) – ķermeņa masa, \(g\) – brīvās krišanas paātrinājums, kas tuvu Zemes virsmai vienāds ar \(9,8\space\mathrm{m/s^2}\) jeb aptuveni \(10\space\mathrm{m/s^2}\).
Aprēķini:
\(F_\mathrm{sm}=mg=17\space\mathrm{kg}\cdot9,8\space\mathrm{m/s^2}\approx167\space\mathrm N\) vai \(F_\mathrm{sm}=mg=17\space\mathrm{kg}\cdot10\space\mathrm{m/s^2}=170\space\mathrm N\). Abus rezultātus noapaļo līdz diviem zīmīgajiem cipariem, atstājot tik zīmīgos ciparus, cik to ir dotajos lielumos.
Atbilde: uz lidaparātu darbojas \(1,7\cdot10^2\space\mathrm N\) liels smaguma spēks.
4.
Uz Mēness dronu lidojumam nevar izmantot. Uz Mēness nav atmosfēras, tādēļ nevar rasties spārnu cēlējspēks. Lidaparāts var lidot virs Mēness virsmas tikai izmantojot reaktīvo dzinēju.
Vērtēšanas kritēriji
1.
Zina ceļa aprēķina formulu un saskaņo mērvienības – 1 punkts.
Aprēķina drona veikto ceļu, noapaļo rezultātu un pieraksta to ar mērvienību – 1 punkts.
2.
Vērtē līmeņos
Attēlo spēkus zīmējumā, pieraksta spēku nosaukumus. Pieļauj ne vairāk kā vienu neprecizitāti spēka nosaukumā – 2 punkti.
Attēlo zīmējumā tikai trīs spēkus vai pieļauj divas neprecizitātes spēku nosaukumos, vai neuzraksta divu spēku nosaukumus – 1 punkts.
Attēlo zīmējumā tikai divus spēkus vai pieļauj trīs neprecizitātes spēku nosaukumos, vai neuzraksta trīs spēku nosaukumus – 0 punkti.
3.
Zina vai atrod formulu lapā smaguma spēka aprēķināšanas formulu, veic aprēķinu, noapaļo rezultātu un pieraksta atbildi ar mērvienībām – 1 punkts.
4.
Skaidro, kāpēc dronu nevar izmantot uz Mēness – 1 punkts.