Lodīte uzsāk vienmērīgi paātrinātu kustību pa horizontālu virsmu gar \(1\space\mathrm m\) garu lineālu. Lodītes stāvokļi fotografēti ik pēc \(0,1\space\mathrm s\).
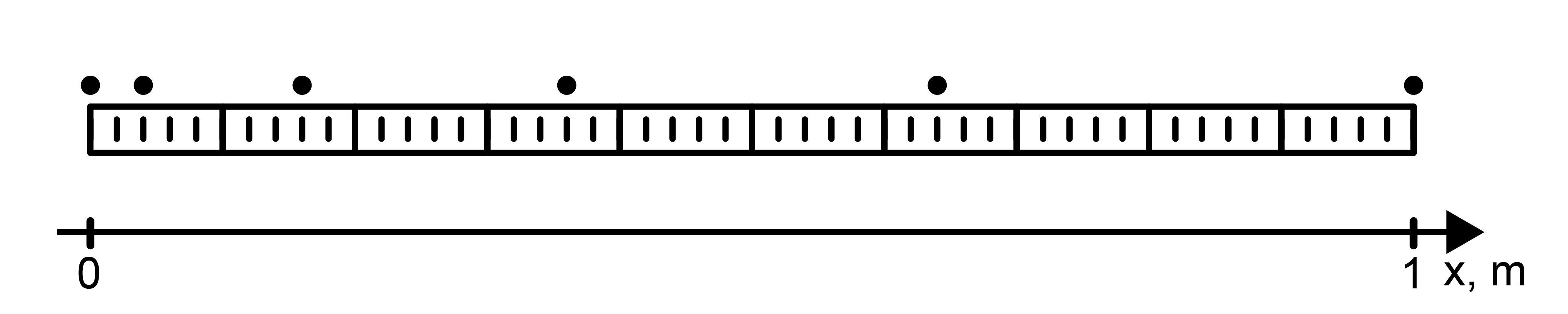
Aprēķini lodītes paātrinājuma projekciju un parādi aprēķinu gaitu!
Cik liels ir ātruma modulis pēc \(0,35\space\mathrm s\)?
Dotajā attēlā iezīmē lodītes stāvokli pēc \(0,35\space\mathrm s\)!
Vienmērīgi paātrinātajā taisnlīnijas kustībā lodītes koordinātas \(x\) maiņu laikā \(t\) apraksta vienādojums \(x=x_0+v_{\mathrm{0x}}+\frac{a_{\mathrm x}t^2}{2}\), kur \(x_0\) – lodītes sākuma koordināta, \(v_{\mathrm{0x}}\) – lodītes sākuma ātruma projekcija, \(a_{\mathrm x}\) – lodītes paātrinājuma projekcija.
No uzdevuma teksta ir skaidrs, ka \(x_0=0\) un \(v_{\mathrm{0x}}=0\). Tādēļ lodītes koordinātas vienādojumu var uzrakstīt formā \(x=\frac{a_{\mathrm x}t^2}{2}\). No vienādojuma izsaka paātrinājuma projekciju \(a_{\mathrm{x}}=\frac{2x}{t^2}\).
Lai aprēķinātu paātrinājumu, no attēla nolasa kustības laiku un atbilstošo koordinātu. Attēlā laika momenti atzīmēti ar sarkanu krāsu, bet tiem atbilstošās koordinātu vērtības – ar zilu krāsu (skatīt attēlu). Attālumu skalas jeb \(x\) ass iedaļas vērtība ir 0,2 m.
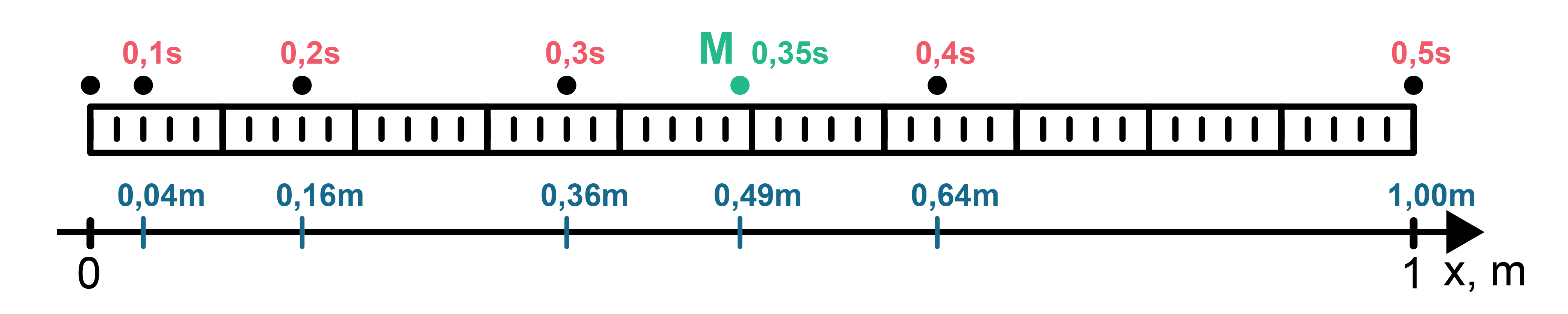
Ātruma moduli aprēķina no ātruma projekcijas \(v_{\mathrm{x}}\) vienādojuma. No fizikas formulu lapas izraksta izteiksmi \(a_{\mathrm x}=\frac{v_{\mathrm x}-v_{\mathrm{0x}}}{t}\), izsaka \(v_{\mathrm{x}}=v_{\mathrm{0x}}+a_{\mathrm{x}}t\). Ir zināms, ka \(v_{\mathrm{0x}}=0\), tādēļ \(v_{\mathrm{x}}=a_{\mathrm{x}}t\). Gan ātruma projekcija, gan paātrinājuma projekcija ir pozitīvas, tādēļ formulu var uzrakstīt ar moduļiem \(v=at\).
Lodītes koordināta laikā \(t=0,35\space\mathrm s\) atzīmēta attēlā ar burtu M.
Aprēķini:
\(a_{\mathrm{x}}=\frac{2x}{t^2}=\frac{2\cdot0,4}{0,1^2}=8\space\mathrm {m/s^2}\)
Piezīme: tā kā uzdevumā ir teikts, ka kustība ir vienmērīgi paātrināta, paātrinājuma noteikšanai var izmantot jebkura stroboskopiskā attēla punkta laika un koordinātes vērtība, iegūstot rezultātā vienu un to pašu paātrinājuma vērtību.
\(v=at=8\cdot0,35=2,8\space\mathrm {m/s}\)
\(x=\frac{a_{\mathrm x}t^2}{2}=\frac{8\cdot0,35^2}{2}=0,49\space\mathrm{m}\)
Atbilde: lodītes paātrinājums ir \(8\space\mathrm {m/s^2}\), ātrums pēc \(0,35\space\mathrm s\) ir \(2,8\space\mathrm{m/s}\) bet koordināta \(0,49\space\mathrm{m}\).
Vērtēšanas kritēriji
Iegūst informāciju no uzdevuma teksta un attēla un saista lodītes stāvokļus ar tās koordinātām. Uzraksta koordinātas vienādojumu – 1 punkts.
Izsaka paātrinājuma projekciju no koordinātas vienādojuma – 1 punkts.
Iegūst skaitlisko informāciju no zīmējuma un aprēķina paātrinājuma skaitlisko vērtību. Pieraksta paātrinājuma mērvienības – 1 punkts.
Aprēķina lodītes koordinātu pēc \(0,35\space\mathrm s\) un pieraksta koordinātu ar mērvienībām – 1 punkts.
Iezīmē koordinātu dotajā attēlā – 1 punkts.