No stāvas klints, kuras augstums virs ūdens ir \(h\), horizontāli izsviež akmeni, kura masa ir \(m\). Akmens sākuma ātruma modulis ir \(v_0\). Brīvās krišanas paātrinājuma modulis ir \(g\). Gaisa pretestību neņem vērā! Uzdevuma risinājumā izmanto tikai dotos apzīmējumus!
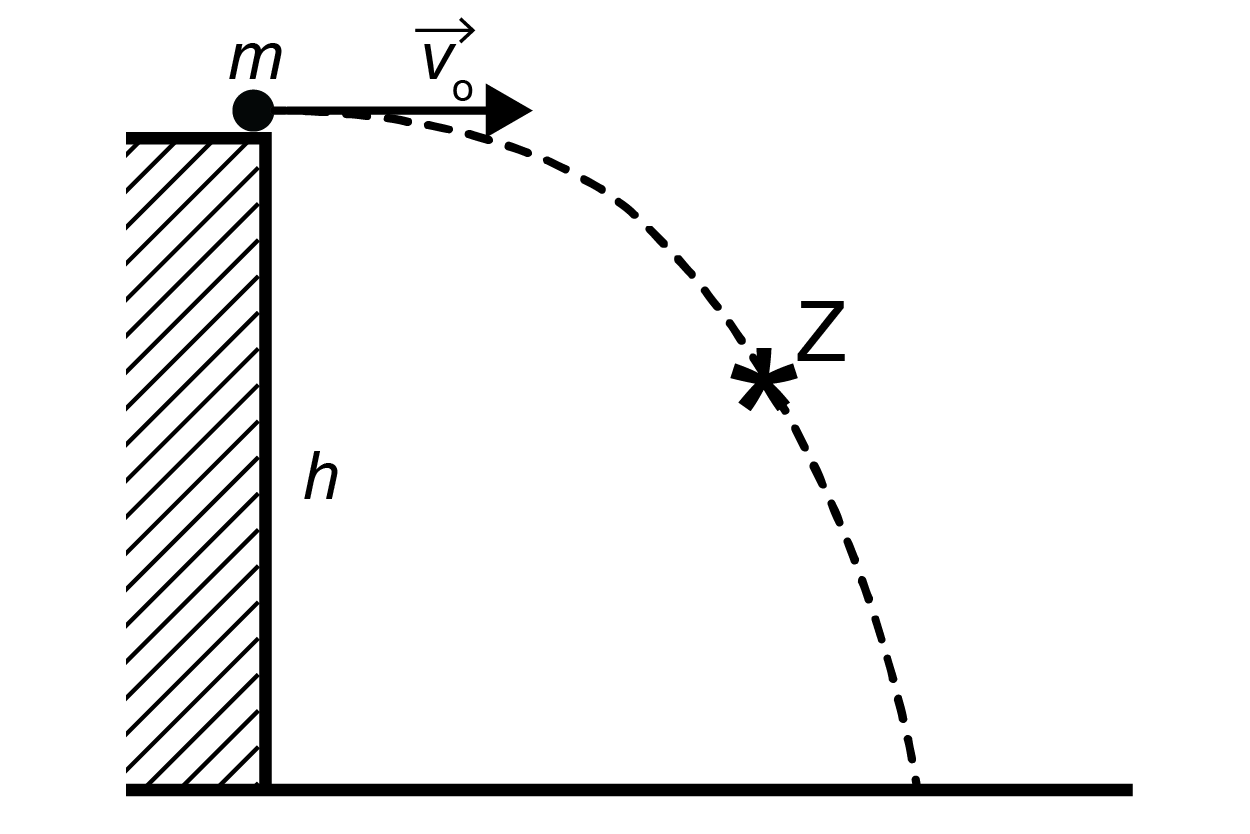
Dotajā zīmējumā attēlo rezultējošā ātruma \(\overrightarrow{v}\) vektoru punktā Z! Mērogu var neievērot.
Akmens sasniedz ūdens virsmu pēc laika \(t\). Izmantojot nepieciešamos dotos lielumus, iegūsti formulu laika \(t\) aprēķināšanai!
Akmens kinētiskā enerģija īsi pirms ūdens virsmas sasniegšanas ir \(W_{\mathrm k}\). Izmantojot tikai dotos lielumus, uzraksti atbilstošu vienādojumu \(W_{\mathrm k}\) aprēķināšanai!
Akmens ātrums \(\overrightarrow v\) punktā Z ir vērsts lidojuma trajektorijas pieskares virzienā (skatīt attēlu). Lidojuma laikā akmens potenciālā enerģija samazinās, pārejot kinētiskajā enerģijā. Tādēļ Z punktā akmens ātruma modulis ir lielāks, nekā izsviešanas punktā \(|\overrightarrow {v}|>|\overrightarrow {v_0}|\).
.png)
Uz horizontālā virzienā izsviesto akmeni iedarbojas tikai smaguma spēks, kas piešķir akmenim lejup vērstu brīvās krišanas paātrinājumu \(\overrightarrow g\). Akmens kustība horizontālajā virzienā ir vienmērīga taisnlīnijas kustība, bet vertikālajā virzienā - brīvā krišana bez sākuma ātruma. Tādā gadījumā kustības pārvietojuma moduli nosaka pēc izteiksmes \(h=\frac{gt^2}{2}\), no kuras izsaka akmens krišanas laiku \(t=\sqrt{\frac{2h}{g}}\).
Akmenim trajektorijas sākuma punktā Z piemīt pilnā mehāniska enerģija \(W_{\mathrm{pilna}}\), kas ir kinētiskās enerģijas \(\frac{mv_{\mathrm0}^2}{2}\) un potenciālās enerģijas \(mgh\) summa:
\(W_{\mathrm{pilna}}=\frac{mv_{\mathrm{0}}^2}{2}+mgh\).
Tieši pie ūdens virsmas akmens augstums ir vienāds ar nulli. Tādēļ akmens pilnā mehāniskā enerģija \(W_{\mathrm{pilna}}\) pie ūdens virsmas kļūst vienāda ar akmens kinētisko enerģiju \(W_{\mathrm k}\). Saskaņā ar mehāniskās enerģijas nezūdamības likumu kinētiskā enerģija īsi pirms ūdens virsmas sasniegšanas ir \(W_{\mathrm{k}}=\frac{mv_{\mathrm{0}}^2}{2}+mgh\).
Atbilde: rezultējošais ātrums punktā Z ir vērsts pa trajektorijas pieskari (skatīt attēlu). Krišanas laiku nosaka pēc formulas \(t=\sqrt{\frac{2h}{g}}\). Īsi pirms ūdens virsmas sasniegšanas akmens kinētiskā enerģija ir \(W_{\mathrm{k}}=\frac{mv_{\mathrm{0}}^2}{2}+mgh\).
Vērtēšanas kritēriji
Zina, ka līklīnijas kustībā jebkurā punktā ātrums ir vērsts pa trajektorijas pieskari. Attēlo rezultējošā ātruma vektoru punktā Z – 1 punkts.
Zina, ka horizontāli mesta ķermeņa kustība ir salikta – vienmērīga kustība horizontālajā virzienā un vienmērīgi paātrināta kustība vertikālajā virzienā. No vienmērīgi paātrinātās kustības likumsakarībām izsaka kustības laiku – 1 punkts.
Izmanto pilnās mehāniskās enerģijas nezūdamības likumu un iegūst formulu akmens kinētiskās enerģijas aprēķināšanai īsi pirms ūdens virsmas sasniegšanas, izmantojot tikai uzdevumā dotos lielumus – 1 punkts.