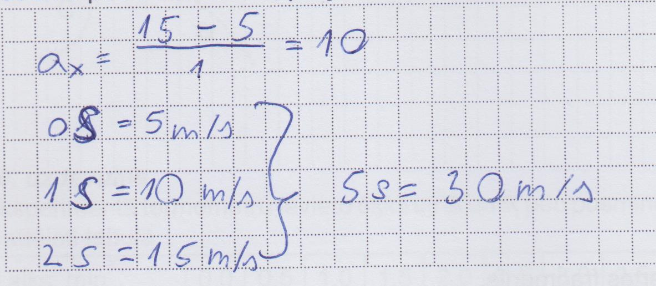Attēlā parādīta sporta automobiļa ātruma projekcijas maiņa atkarībā no laika.
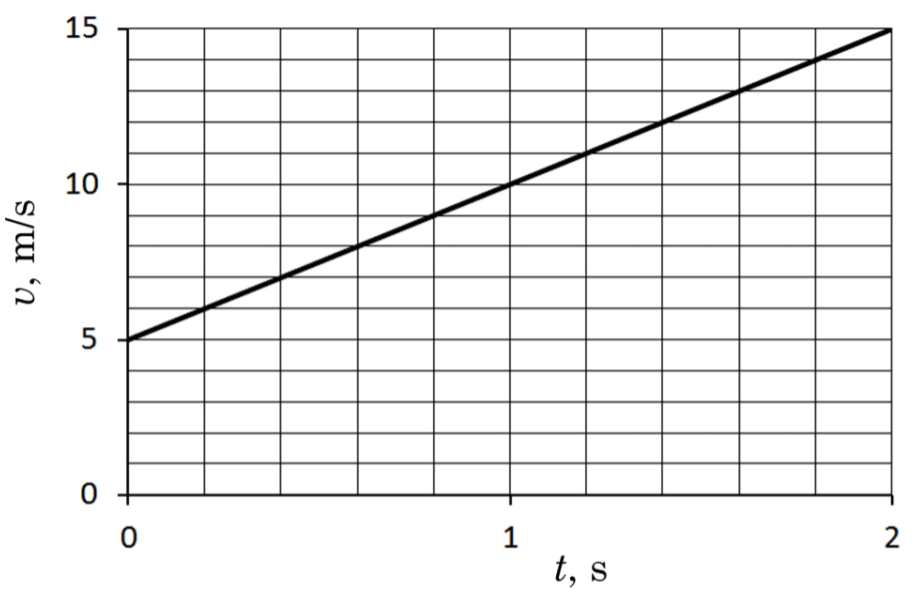
Izmantojot grafikā sniegto informāciju, uzraksti ātruma projekcijas aprēķināšanas vienādojumu un aprēķini ātrumu pēc 5 sekundēm, pieņemot, ka kustības raksturs nemainās!
No paātrinājuma definīcijas \(a_{\mathrm{x}}=\frac{v_{\mathrm{x}}-v_{\mathrm{0x}}}{t}\) izsaka ātruma projekcijas vienādojumu \(v_{\mathrm{x}}=v_{\mathrm{0x}}+at\), kur \(v_{\mathrm{0x}}\) – sākuma ātruma projekcija, \(a_{\mathrm{x}}\) – paātrinājuma projekcija, \(t\)– kustības laiks. Iegūtais vienādojums ir vienmērīgi paātrinātas kustības ātruma vienādojums vispārīgā veidā. No grafika nolasa, ka sākuma ātruma projekcija \(v_{\mathrm{0x}}=5\space \mathrm{m/s}\).
Paātrinājuma projekciju aprēķina no paātrinājuma definīcijas \(a_{\mathrm{x}}=\frac{v_{\mathrm{x}}-v_{\mathrm{0x}}}{t}\). No grafika nolasa ātruma projekcijas \(v_{\mathrm{x}}\) skaitlisko vērtību laika momentā \(t\). Attēlā redzams, ka laika momentā \(t=2\space \mathrm{s}\) ātruma projekcija ir \(v_{\mathrm{x}}=15 \space \mathrm{m/s}\). Paātrinājuma projekcija \(a_{\mathrm{x}}=\frac{15-5}{2}=5 \space\mathrm{m/s^2}\).
Konkrētajai kustībai atbilst ātruma projekcijas vienādojums: \(v_{\mathrm{x}}=5+5t\).
Ātruma projekciju pēc 5 sekundēm nosaka no vienādojuma \(v_{\mathrm{x}}=5+5\cdot5=30\space\mathrm{m/s}\).
Atbilde: ātruma projekcijas vienādojums \(v_{\mathrm{x}}=5+5t\). Ātrums pēc 5 sekundēm ir \(30\space\mathrm{m/s}\).
Vērtēšanas kritēriji
Nolasa no grafika nepieciešamos lielumus un aprēķina kustības paātrinājumu – 1 punkts.
No paātrinājuma definīcijas izsaka kustības beigu ātrumu un iegūst kustības ātruma vienādojumu vispārīgā veidā. Ievieto skaitļus un aprēķina ātrumu pēc 5 sekundēm – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
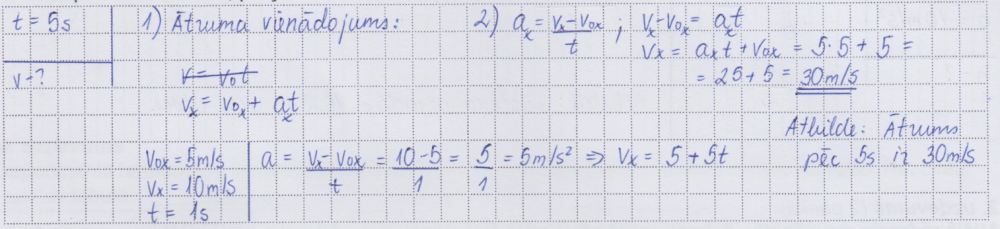
2. piemērs: risinājums novērtēts ar 2 punktiem.

3. piemērs: risinājums novērtēts ar 1 punktu - skolēns neparāda, kā nosaka paātrinājumu.
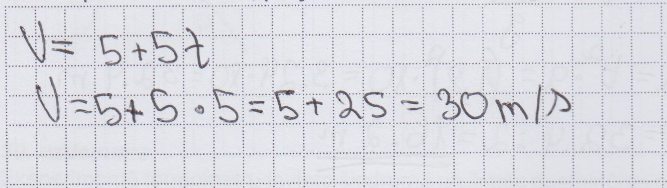
4. piemērs: risinājums novērtēts ar 0 punktiem - kaut skolēns nolasa datus no grafika un, logiski spriežot, iegūst pareizo ātruma skaitlisko vērtību, netiek neizmants ātruma vienādojums un atrisinājuma pirmajā rindiņā noteiktais paātrinājums ir pretrunā ar talāk uzrakstīto rezultātu, kas liecina par paātrinājuma jēdziena neizpratni.