Mārtiņš, gatavojot prezentāciju, veica audioierakstu, kurā nejauši „iekļuva” trokšņi no ielas – pirmais, kad no jumta malas atlūza lāsteka, un otrais, kad tā sašķīda pret ietvi. No ieraksta Mārtiņš noteica, ka starp šiem trokšņiem ir pagājušas 1,8 sekundes.
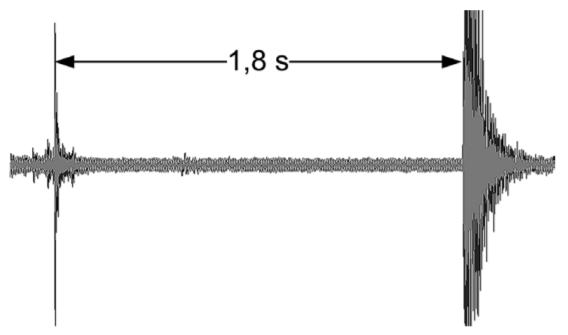
Novērtē, cik augstu virs ietves atradās lāsteka, pirms tā atlūza no jumta malas! g = 10 m/s2.
Lāstekas krišanu var uzskatīt par vienmērīgi paātrinātu kustību.
Kustības pārvietojuma moduli \(s\) nosaka pēc vienādojuma \(s=v_0t+\frac{at^2}{2}\), kur \(v_0\) – lāstekas sākuma ātrums, \(a\) – kustības paātrinājums, \(t\)– kustības laiks. No uzdevuma teksta ir skaidrs, ka lāstekas sākuma ātrums \(v_0=0\), paātrinājums \(a\) ir brīvās krišanas paātrinājums \(g\). Pārvietojuma moduli \(s\) dotajā gadījumā apzīmē ar \(h\).
Iegūst izteiksmi \(h=\frac{gt^2}{2}\).
Aprēķini:
\(h=\frac{gt^2}{2}=\frac{10\cdot1,8^2}{2}=16,2\space \mathrm m\approx16\space \mathrm m\).
Atbilde: lāstekas augstums virs ietves ir aptuveni 16 m.
Vērtēšanas kritēriji
Zina vai atrod formulu lapā formulu lāstekas krišanas augstuma aprēķināšanai, ja tās sākuma ātrums ir nulle – 1 punkts.
Veic aprēķinu un iegūst rezultātu ar vajadzīgo zīmīgo ciparu skaitu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.

2. piemērs: risinājums novērtēts ar 2 punktiem.

3. piemērs: risinājums novērtēts ar 0 punktiem.

4. piemērs: risinājums novērtēts ar 0 punktiem.