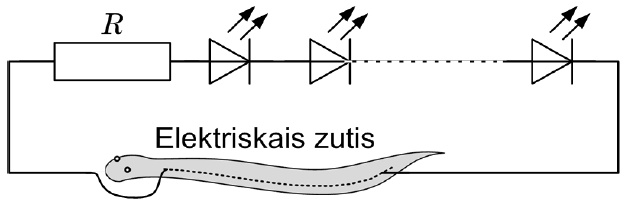
Skolas zinātnes centrs iegādājās elektriskā zuša modeli. Mikus nolēma to izmantot kā sprieguma avotu Ziemassvētku rotājuma izgatavošanai. Mikus zuša modelim pieslēdza rezistoru \(R=3\space\mathrm{k\Omega}\) un daudzu LED spuldzīšu virteni. Spriegums uz katras spuldzītes ir 2,0 V un caur tām plūst 30 mA stipra strāva. Spriegums starp zuša modeļa galvu un asti ir 490 V.
1. Cik liels ir spriegums uz rezistora R?
2. Cik liels ir spriegums starp spuldzīšu virtenes galiem?
3. Cik spuldzīšu Mikus ir saslēdzis virtenē?
4. Lai pārbaudītu virtenē lietojamo LED spuldzīšu darbību, Mikus izveidoja slēgumu.
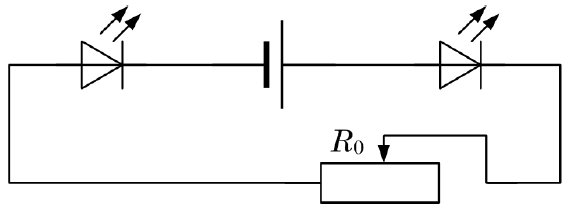
Normālai darbībai katrai spuldzītei nepieciešams spriegums 2,0 V, lai spuldzītē plūstu 30 mA stipra strāva.
Kādai jābūt reostata pretestībai \(R_{\mathrm 0}\), ja strāvas avota EDS ir 4,5 V un tā iekšējā pretestība \(1,3\space\mathrm{\Omega}\)?
1. Elektriskais zutis ar rezistoru un spuldzēm veido virknes slēgumu. Tādēļ strāvas stiprums \(I\) ķēdē visur ir vienāds. Spriegumu starp rezistora spailēm \(U\) nosaka, izmantojot Oma likuma formulu ķēdes posmam \(I=\frac{U}{R}\), kur \(R\) – rezistora pretestība. No formulas izsaka \(U=IR\).
Strāvas stiprumu \(I\) izsaka ampēros: \(30\space\mathrm{mA}=30\cdot 10^{-3}\space\mathrm A\). Rezistora pretestību \(R\) izsaka omos: \(3\space\mathrm{k\Omega}=3\cdot 10^3\space\mathrm{\Omega}\).
Aprēķini: \(U=IR=30\cdot 10^{-3}\cdot 3\cdot 10^3=90\space\mathrm V\).
Atbilde: spriegums uz rezistora spailēm ir \(90\space\mathrm V\).
2. Zīmējumā (skatīt 1. attēlu) iezīmēti četri punkti. Spriegums starp punktiem 1 un 2 ir vienāds ar spriegumu \(U\) starp rezistora spailēm, kas ir \(90\space\mathrm V\). Spriegums starp punktiem 2 un 3 ir spriegums starp spuldzīšu virtenes galiem \(U_\mathrm{sp}\). Spriegums starp punktiem 1 un 4 ir spriegums \(U_\mathrm {zut}\) – spriegums starp zuša modeļa galvu un asti, kas pēc dotā ir vienāds ar \(490\space\mathrm V\).
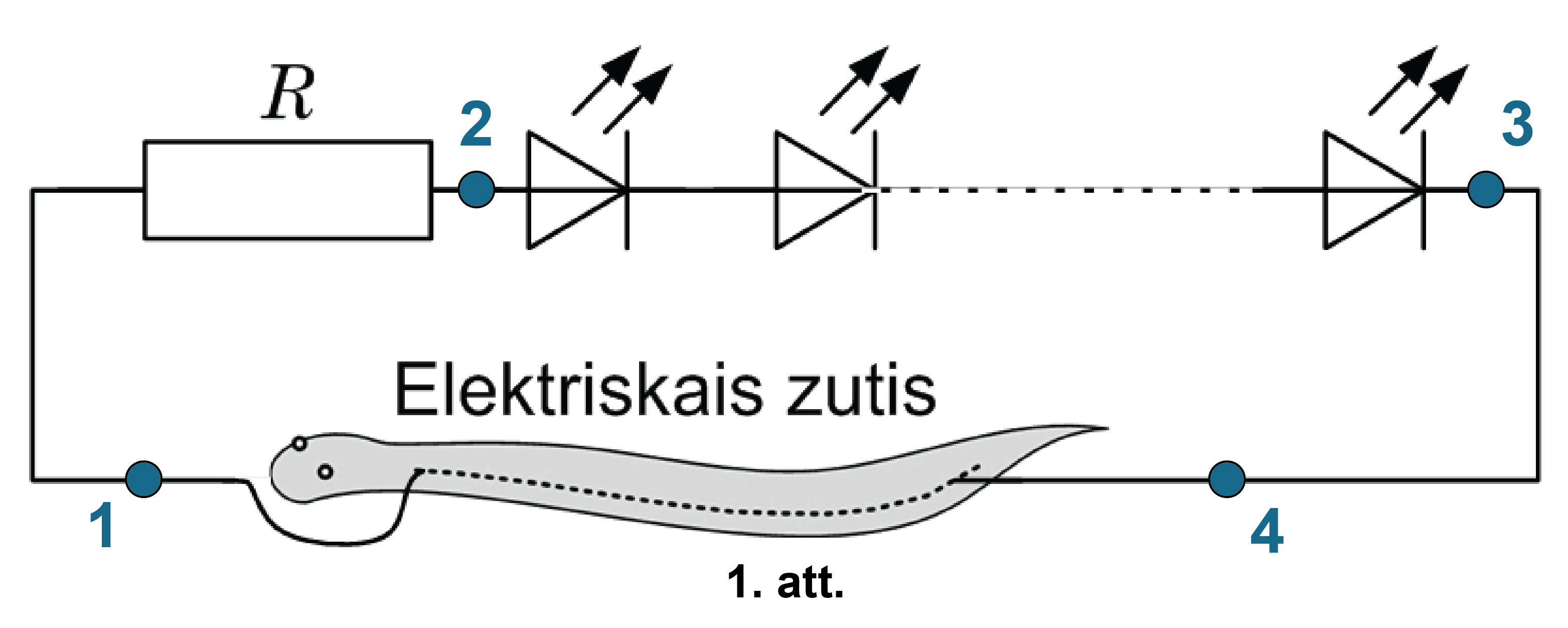
Ķēdē zutis, spuldzīšu virtene un rezistors saslēgti virknē. Tādēļ ir spēkā sakarība starp spriegumiem: \(U_\mathrm{zut}=U_\mathrm{sp}+U\). Izsaka spriegumu \(U_\mathrm{sp}\) starp spuldzīšu virtenes galiem: \(U_\mathrm{sp}=U_\mathrm{zut}-U\).
Aprēķini:
\(U_\mathrm{sp}=U_\mathrm{zut}-U=490-90=400\space\mathrm V\).
Atbilde: spriegums starp spuldzīšu virtenes spailēm \(400\space\mathrm V\).
3. \(N\) vienādas spuldzītes savienotas virknē. Spriegums starp katras spuldzītes spailēm ir \(U_0=2\space\mathrm V\). Spriegums starp spuldzīšu virtenes galiem \(U_\mathrm{sp}=400\space\mathrm V\). Tātad, \(U_\mathrm{sp}=NU_0\space\implies\space N=\frac{U_\mathrm{sp}}{U_0}\).
Aprēķini: \(N=\frac{U_\mathrm{sp}}{U_0}=\frac{400}{2}=200\).
Atbilde: Mikus ir saslēdzis virtenē 200 spuldzītes.
4. Reostats, divas spuldzes un strāvas avots ir saslēgti virknē (skatīt 2. attēlu). Pielieto Oma likuma formulu pilnai ķēdei \(I=\frac{\mathscr E}{R+r}\), kur \(R\) – ārējās ķēdes kopējā pretestība, bet \(r\) – strāvas avota iekšējā pretestība. Ārējā ķēde sastāv no reostata un divām spuldzēm. Tādēļ \(R=R_0+2R_\mathrm{sp}\). Ievietojot šo izteiksmi Oma likuma formulā, iegūst \(I=\frac{\mathscr E}{R_0+2R_\mathrm{sp}+r}\).
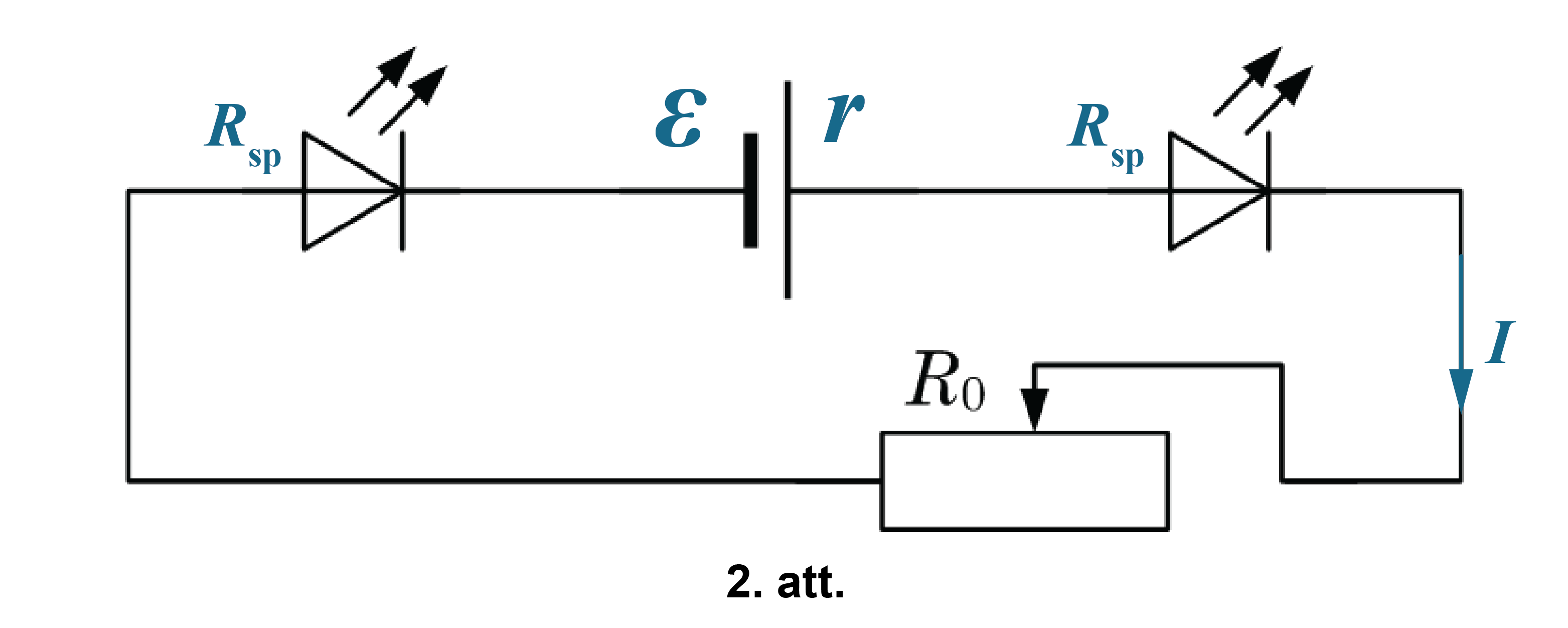
Tālāk var rēķināt dažādi.
1. variants.
No formulas \(I=\frac{\mathscr E}{R_0+2R_\mathrm{sp}+r}\) izsaka strāvas avota EDS: \(\mathscr E=I(R_o+2R_\mathrm{sp}+r)=IR_0+2IR_\mathrm{sp}+Ir\).
Ievērojot, ka izteiksme \(IR_\mathrm{sp}\) ir spriegums starp spuldzītes spailēm \(U_\mathrm{sp}=2\space\mathrm V\):
\(\mathscr E=IR_0+2U_\mathrm{sp}+Ir\space\implies\space R_0=\frac{\mathscr E-2U_\mathrm{sp}-Ir}{I}\).
Aprēķini:
\(R_0=\frac{\mathscr E-2U_\mathrm{sp}-Ir}{I}=\frac{4,5-2\cdot2-30\cdot10^{-3}\cdot1,3}{30\cdot10^{-3}}\approx15,4\space\Omega\approx15\space\Omega\).
2. variants.
No formulas \(I=\frac{\mathscr E}{R_0+2R_\mathrm{sp}+r}\) izsaka reostata pretestību \(R_0=\frac{\mathscr E}{I}-2R_\mathrm{sp}-r\). Nav zināma spuldzītes pretestība \(R_\mathrm{sp}\). To nosaka no Oma likuma ķēdes posmam \(I=\frac{U_\mathrm{sp}}{R_\mathrm{sp}}\), kur \(U_\mathrm{sp}=2\space\mathrm V\) un \(I=30\cdot 10^{-3}\space\mathrm A\). Spuldzītes pretestība \(R_\mathrm{sp}=\frac{U_\mathrm{sp}}{I}\).
Aprēķini:
\(R_\mathrm{sp}=\frac{U_\mathrm{sp}}{I}=\frac{2}{30\cdot 10^{-3}}\approx66,7\space\Omega\).
\(R_0=\frac{\mathscr E}{I}-2R_\mathrm{sp}-r=\frac{4,5}{30\cdot10^{-3}}-2\cdot66,7-1,3\approx15,3\space\Omega\approx\space 15\Omega\)
Atbilde: reostata pretestība ir \(15\space\Omega\).
Vērtēšanas kritēriji
1. Zina, ka virknes slēgumā strāvas stiprums visā ķēdē ir vienāds. Zina vai atrod formulu lapā Oma likuma ķēdes posmam formulu. Saskaņo mērvienības un aprēķina spriegumu uz rezistora. Rezultātu pieraksta ar mērvienību – 1 punkts.
2. Zina, ka virknes slēgumā strāvas stiprums visā ķēdē ir vienāds. Zina, ka virknes slēgumā kopējo spriegumu ārējā ķēdē veido virknē saslēgto patērētāju spriegumu summa. Aprēķina spriegumu uz spuldzīšu virtenes galiem – 1 punkts.
3. Zina, ka virknes slēgumā strāvas stiprums visā ķēdē ir vienāds. Zina, ka virknes slēgumā kopējo spriegumu veido atsevišķo posmu spriegumu summa. Aprēķina spriegumu uz spuldzīšu virtenes galiem – 1 punkts.
4.
Zina, kā virknes slēgumā nosaka kopējo pretestību – 1 punkts.
Zina vai atrod formulu lapā Oma likuma matemātisko izteiksmi pilnai ķēdei – 1 punkts.
Veic matemātiskās darbības un izsaka meklējamo lielumu – 1 punkts.
Saskaņo lielumu mērvienības, veic aprēķinus – 1 punkts.