Cilindrā ieslēgtās ideālās gāzes tilpums ir \(V=0,5\cdot10^{-3}\space\mathrm{m^3}\), spiediens ir \(p=20\cdot10^{4}\space\mathrm{Pa}\) un temperatūra \(T=290\space\mathrm{K}\).
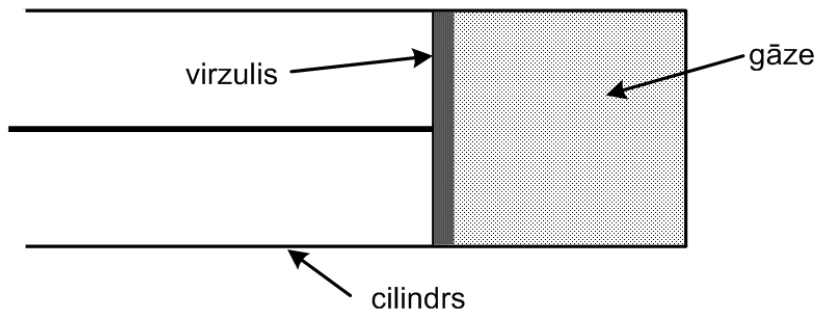
Virzuli lēnām pārvieto pa kreisi. Gāzes temperatūra nemainās. Attēlo grafiski gāzes spiediena maiņu atkarībā no tilpuma!
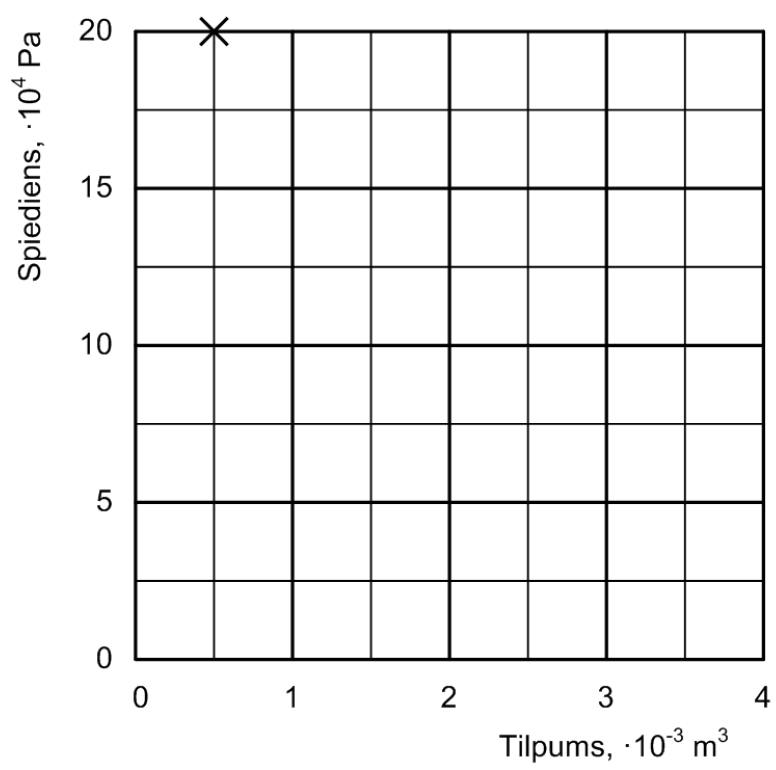
Pieņemot, ka gāzes masa cilindrā nemainās, spēkā ir Klapeirona vienādojums \(\frac{pV}{T}=const\), kur \(p\) – gāzes spiediens, \(V\) – gāzes tilpums, \(T\) – gāzes absolūtā temperatūra.
Lēnām saspiežot gāzi, tās temperatūra nemainās, process ir izotermisks. Tādēļ ir spēkā Boila–Mariota likums \(pV=const\). Tas nozīmē, ka reizinājums \(pV\) visos gāzes stāvokļos ir nemainīgs: \(pV=20\cdot10^5\space\mathrm{Pa}\cdot0,5\cdot10^{-3}\space\mathrm{m^3}=1\cdot10^2\space\mathrm{Pa\cdot m^3}\)
Grafika konstruēšanai nepieciešami vairāki punkti. To iegūšanai noteiksim spiedienu \(p \) atbilstošām no grafika sagataves nolasītām tilpuma \(V\) vērtībām.
Aprēķinu piemēri:
\(V_1=1,0\cdot10^{-3}\space \mathrm{m^3}\) \(p_1 V_1=pV\space\implies p_1=\frac{pV}{V_1}=\frac{1\cdot 10^2}{1\cdot10^{-3}}=10\cdot10^4\space\mathrm{Pa}\)
\(V_2=2,0\cdot10^{-3}\space \mathrm{m^3}\) \(p_2 V_2=pV\space\implies p_2=\frac{pV}{V_2}=\frac{1\cdot 10^2}{2\cdot10^{-3}}=5\cdot10^4\space\mathrm{Pa}\)
\(V_3=3,0\cdot10^{-3}\space \mathrm{m^3}\) \(p_3 V_3=pV\space\implies p_3=\frac{pV}{V_3}=\frac{1\cdot 10^2}{3\cdot10^{-3}}\approx 3,3\cdot10^4\space\mathrm{Pa}\)
\(V_4=4,0\cdot10^{-3}\space \mathrm{m^3}\) \(p_4 V_4=pV\space\implies p_4=\frac{pV}{V_4}=\frac{1\cdot 10^2}{4\cdot10^{-3}}=2,5\cdot10^4\space\mathrm{Pa}\)
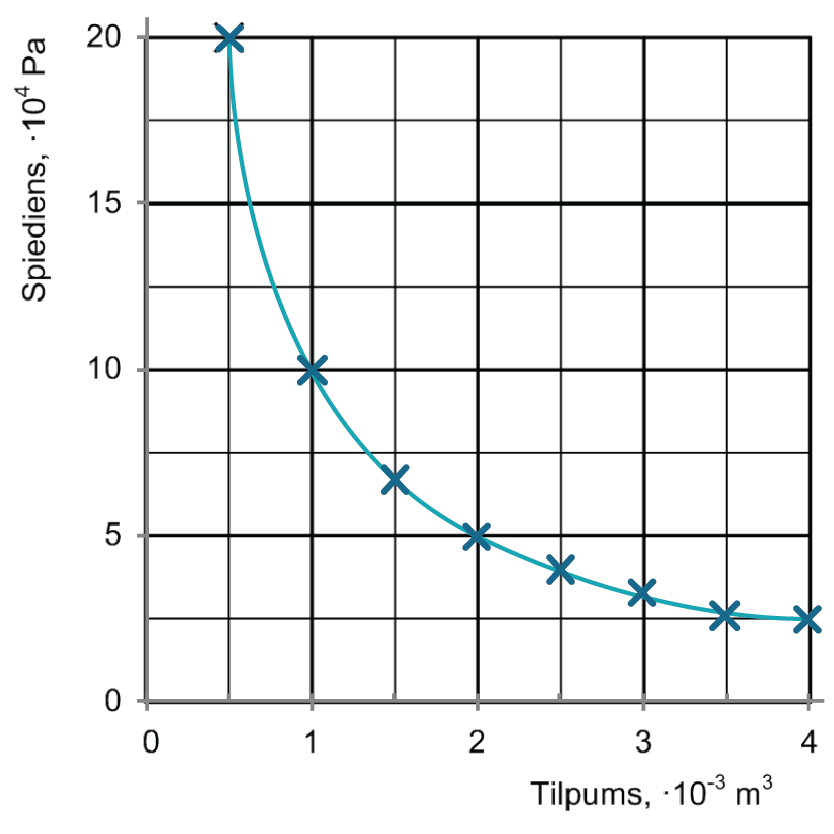
Atliek punktus un konstruē grafika līkni:
Vērtēšanas kritēriji
Zina vai atrod fizikas formulu lapā Klapeirona vienādojuma formulu – 1 punkts.
Aprēķina tilpumam atbilstošās spiediena vērtības – 1 punkts.
Konstruē grafiku – 1 punkts.