Kā mainās sarkanās un zaļās gaismas ātrums, gaismai krītot no gaisa uz plakanparalēlu stikla plāksnīti un izejot no tās? Pieņem, ka gaisam \(n=1,00\)! Atbildi pamato, izmantojot doto grafiku un atbilstošās sakarības!
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Uzdevumā gaisa absolūtais laušanas koeficients ir \(n=1,00\), tāpat kā vakuumam. Vakuumā visi elektromagnētiskie viļņi izplatās ar vienādu ātrumu \(c=3\cdot10^8\space\mathrm{m/s}\). Tādēļ gaisā gan sarkanajai gaismai, gan zaļajai gaismai izplatīšanās ātrums ir \(c\).
Stiklā gaismas izplatīšanās ātrums \(v\) ir atkarīgs no stikla laušanas koeficienta \(n\). Pielieto formulu \(v=\frac{c}{n}\). Tā kā gaismas laušanas koeficients \(n>1\), tad stiklā gaismas izplatīšanās ātrums \(v\) ir mazāks nekā vakuumā.
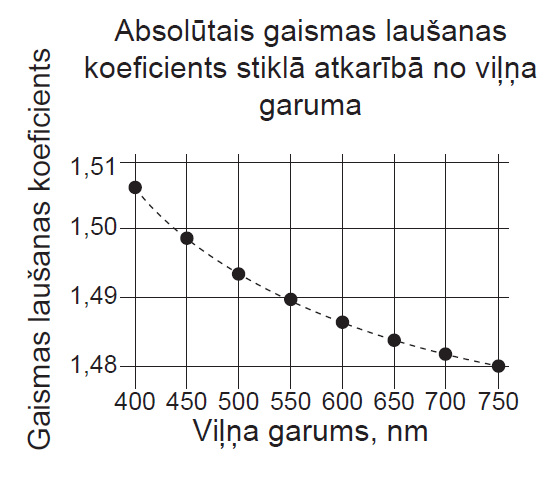
Zināms, ka vides laušanas koeficients ir atkarīgs no viļņa garuma. No elektromagnētisko viļņu skalas atrod sarkanās un zaļās gaismas viļņu garumu (attēlā iezīmēts ar sarkanu un zaļu krāsu). No attēla nolasa, ka sarkanajai gaismai laušanas koeficients \(n_\mathrm s\) stiklā ir par aptuveni \(0,01\) mazāks nekā gaismai laušanas koeficients zaļajai gaismai \(n_\mathrm z\). Tā kā \(n_\mathrm s< n_\mathrm z\)
Atbilde: pirms ieiešanas stikla plāksnītē sarkanā un zaļā gaisma izplatās ar vienādu ātrumu \(c=3\cdot10^8\space\mathrm{m/s}\). Plāksnītē izplatīšanās ātrums gan sarkanajai, gan zaļajai gaismai samazinās, bet vairāk samazinās zaļajai gaismai. Pēc iziešanas no plāksnītes, sarkanās un zaļās gaismas palielinās un atkal kļūst vienāds ar \(c=3\cdot10^8\space\mathrm{m/s}\).
Uzdevuma izpilde eksāmenā - 33,9%.
Vērtēšanas kritēriji
Izmanto gaismas laušanas koeficienta fizikālo jēgu un izskaidro, ka gaismai, pārejot no gaisa stiklā, samazinās ātrums – 1 punkts.
Izmanto elektromagnētisko viļņu skalu un grafiku, lai noteiktu sarkanās un zaļās gaismas ātruma atšķirības stiklā, un paskaidro, ka zaļās gaismas ātrums stiklā samazinās vairāk nekā sarkanās gaismas – 1 punkts.
Secina, ka, pārejot no stikla atpakaļ gaisā, gaismas ātrums palielinās – 1 punkts.