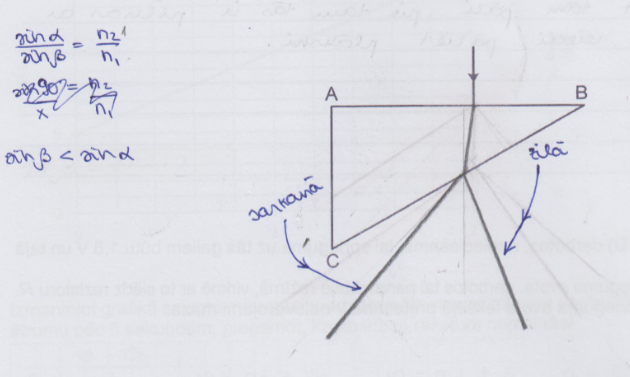
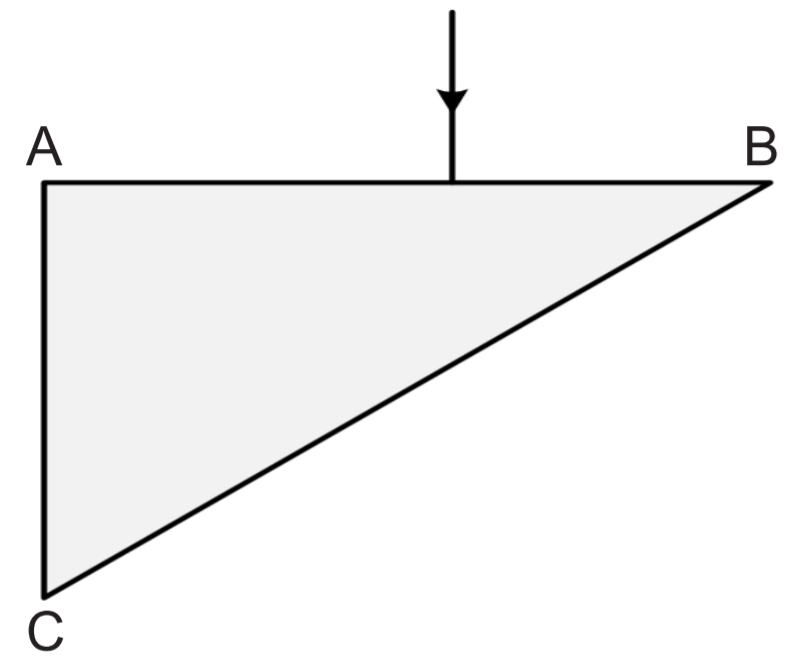
Baltā gaisma no gaisa krīt uz stikla prizmu perpendikulāri prizmas skaldnei AB. Pēc iziešanas no prizmas baltā gaisma sadalās spektrā. Zīmējumā attēlo aptuvenu sarkanās un zilās gaismas staru gaitu! Norādi staru krāsu! Pilnīgās iekšējās atstarošanās robežleņķis ir 42o.
Vispārīgajā gadījumā gaismas laušanas likuma formula: \(\frac{\sin\alpha}{\sin\gamma}=\frac{n_2}{n_1}\), kur \(\alpha\)– krišanas leņķis, \(\gamma\) – laušanas leņķis, \(n_1\) – pirmās vides absolūtais gaismas laušanas koeficients, \(n_2 \)– otrās vides absolūtais gaismas laušanas koeficients.
Punktā M (sk. uzdevuma attēlu) stars pāriet no gaisa stiklā. Tā kā stars krīt perpendikulāri virsmai, tad krišanas leņķis ir nulle. Tādā gadījumā arī laušanas leņķis ir nulle un stara laušana nenotiek.
Pilnīgo iekšējo atstarošanos novēro, ja gaisma pāriet no vides ar lielāku laušanas koeficientu vidē ar mazāku laušanas koeficientu. Uzdevumā šāda situācija ir iespējama K punktā. Uzdevuma tekstā dots pilnīgas iekšējās atstarošanās leņķis stiklam – 42°. Punktā K konstruē perpendikulu un atzīmē krišanas leņķi α (sk. att.1.). Lai saprastu, vai punktā K notiek pilnīgā iekšējā atstarošanās, jānovērtē krišanas leņķis \(\alpha\). Leņķis \(\alpha\) ir vienāds ar leņķi pie virsotnes B trijstūrī ABC. Izmērot uzdevuma zīmējumā malas CB=6 cm un AC=3 cm, nosaka leņķa \(\alpha\) sinusu: \(\sin\alpha=\mathrm{\frac{AC}{CB}}=\frac{3}{6}=0,5\). Tātad, leņķis pie virsotnes B jeb leņķis \(\alpha\)= 30°. Tā kā stara krišanas leņķis K punktā ir mazāks nekā 42°, pilnīgā iekšējā atstarošanās nenotiks un gaismas stars pēc laušanas iziet gaisā.
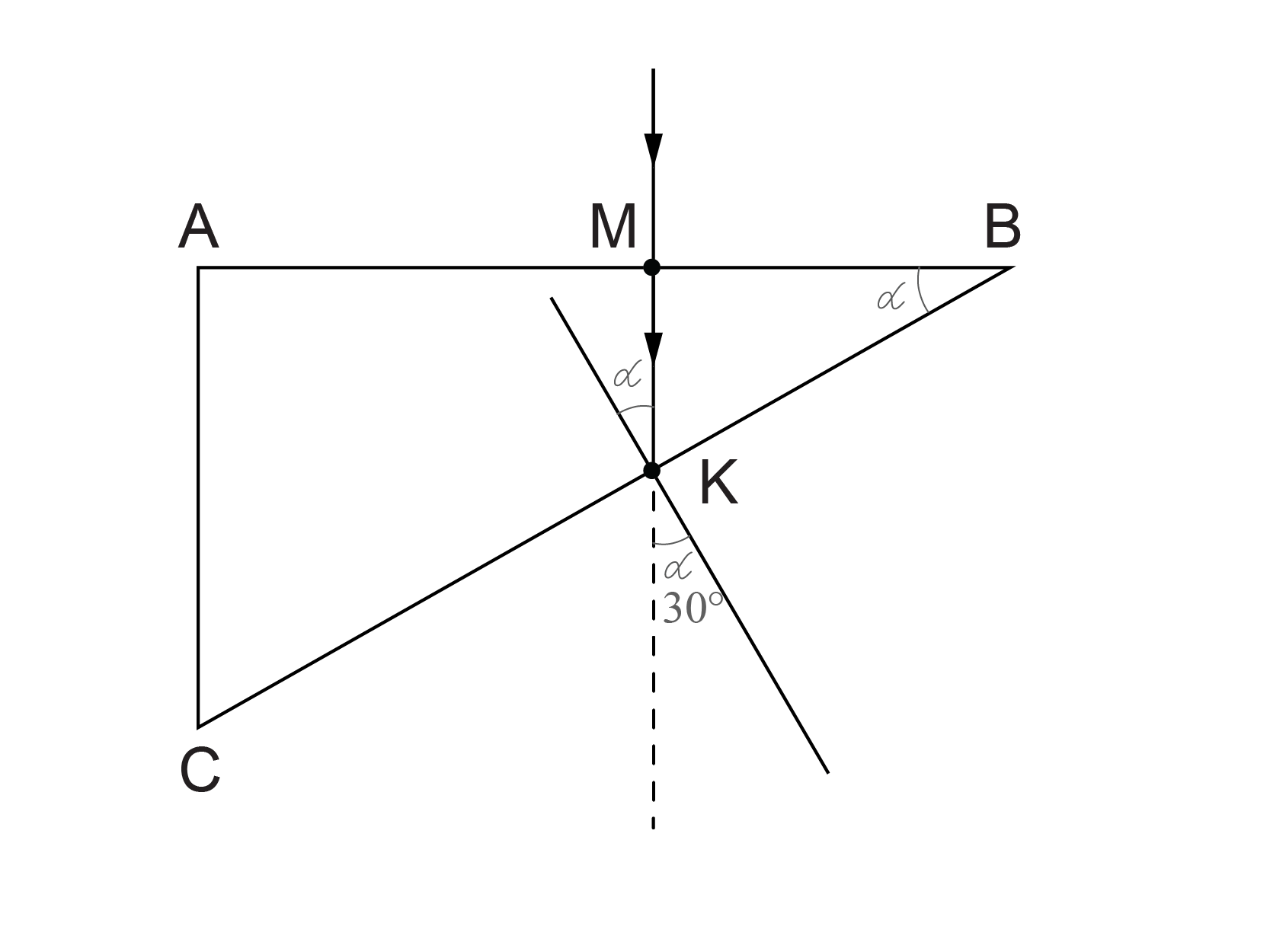
Laušanas likuma formulā punktā K pirmā vide ir stikls ar laušanas koeficientu \(n_1>1\), bet otrā vide – gaiss ar laušanas koeficientu \(n_2\approx1\). Laušanas likuma formula izskatās šādi: \(\frac{\sin30^o}{\sin\gamma}=\frac{n_2}{n_1}\) . Attiecība \(\frac{n_2}{n_1}<1\). Tādēļ attiecība \(\frac{\sin30^o}{\sin\gamma} \) arī mazāka par 1 un \(\sin\gamma>\sin30^o\). Pirmajā kvadrantā sinuss funkcija ir augoša, tādēļ laušanas leņķis \(\gamma>30^o\).
No elektomagnētisko viļņu skalas nolasa, ka sarkanās gaismas viļņa garums apmēram 750 nm, zilās – 400 nm. No dispersijas līknes zināms, ka jo lielāks viļņa garums, jo mazāks gaismas laušanas koeficients. Tāpēc zilās gaismas laušanas koeficients \(n_z\) ir lielāks nekā sarkanās gaismas laušanas koeficients \(n_\mathrm{s}\) (sk. att. 2.)
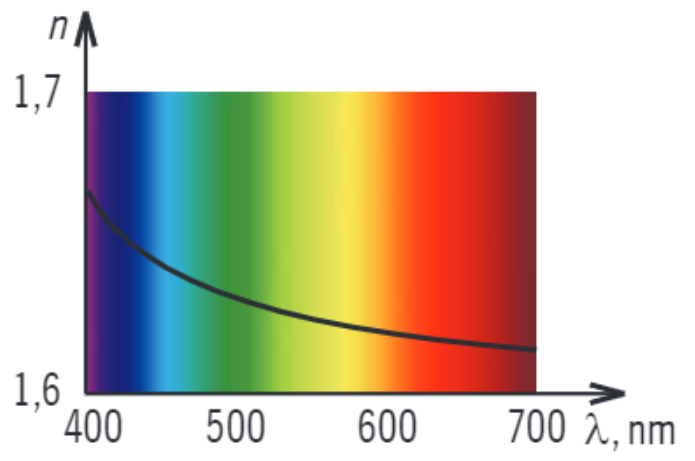
Attēls 2. Gaismas laušanas koeficienta stiklam atkarība no gaismas viļņa garuma (Avots: Fizika 12. klasei. Mācību grāmata. Šilters E., Reguts V., Cābelis A., Vilks I., Lielvārds, 2008.g. 91.lpp.
Pieņemot, ka gaisa laušanas koeficients \(n_2=1\), salīdzina divas formulas \(\frac{\sin30o}{sin\gamma_\mathrm{s}}=\frac{1}{n_\mathrm{s}}\) un \(\frac{\sin30^o}{sin\gamma_\mathrm{z}}=\frac{1}{n_\mathrm{z}}\). Ja \(n_z>n_s\), tad \(\sin\gamma_\mathrm{z}>sin\gamma_\mathrm{s}\) un \(\gamma_\mathrm{z}>\gamma_\mathrm{s}\). Tādēļ zilās gaismas staram laušanas leņķis ir lielāks nekā sarkanās gaismam staram (sk. att.3).
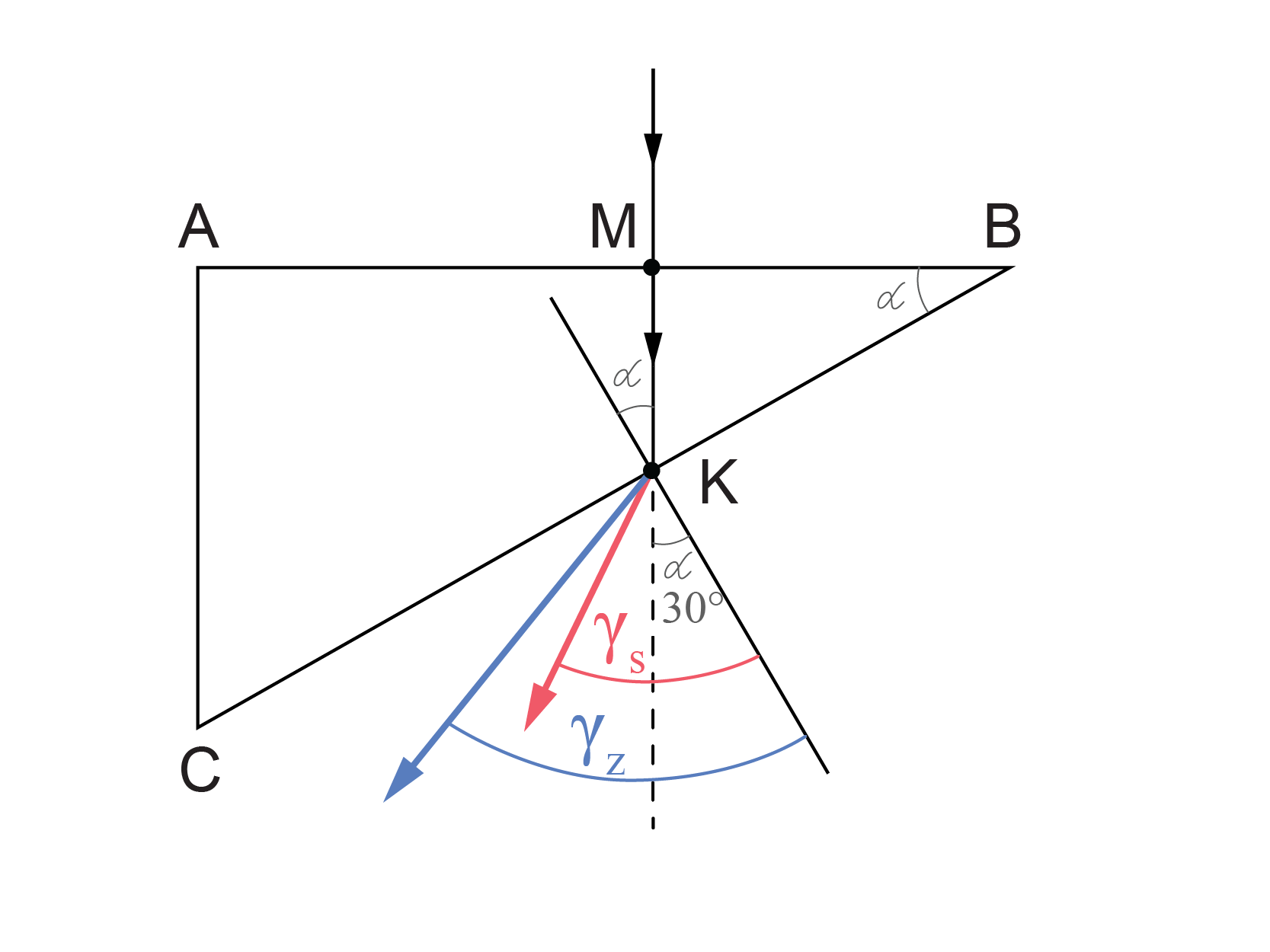
Atbilde: Izejot no prizmas, zilā gaismas stara laušanas leņķis ir lielāks nekā sarkanās gaismas stara laušanas leņķis.
Vērtēšanas kritēriji
Lieto gaismas laušanas likumu un secina, ka gaisma ieiet prizmā bez lūšanas. Attēlo gaismas staru prizmā – 1 punkts.
Pamato, ka nenotiks pilnīgā iekšējā atstarošanās – 1 punkts.
Zina, ka gaismas laušanas leņķis ir atkarīgs no gaismas viļņa garuma. Salīdzina sarkanās un zilās gaismas viļņa garumu. Secina, ka lielāks laušanas koeficients ir zilajai gaismai un tās laušanas leņķis, izejot no prizmas, ir lielāks nekā sarkanās gaismas laušanas leņķis. Attēlo sarkanās un zilās gaismas staru, izejot no prizmas – 1 punkts.
Piezīme: Visos 2. daļas uzdevumos ir jāparāda spriedumu gaita – tas noteikts eksāmena programmā un rakstīts eksāmena darbā.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
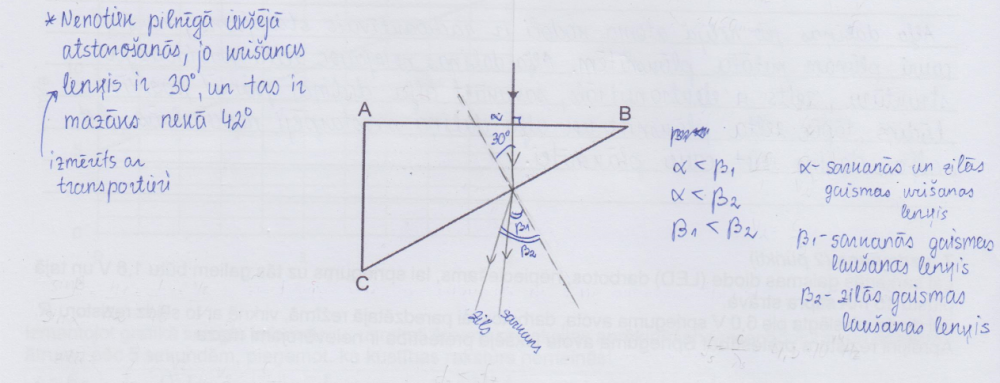
2. piemērs: risinājums novērtēts ar 1 punktu (par staru gaitu, staram ieejot no gaisa stiklā).
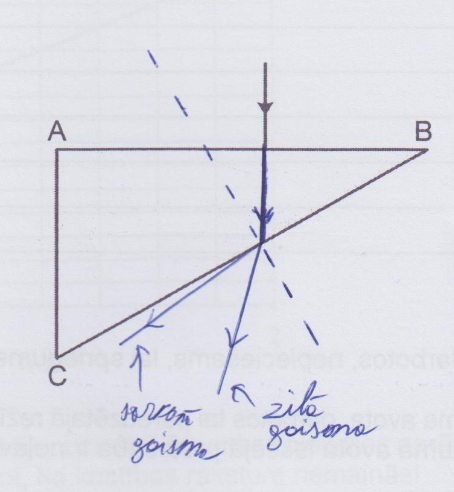
3. piemērs: risinājums novērtēts ar 0 punktiem.
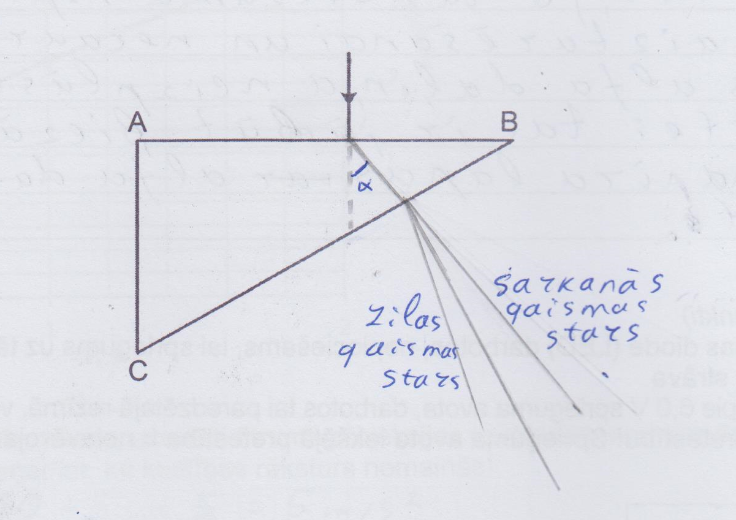
4. piemērs: risinājums novērtēts ar 0 punktiem.