Gaismas stars no gaisa krīt uz prizmas skaldni AB leņķī, kas tikai nedaudz atšķiras no nulles (1. att.). Pēc tam gaismas stara krišanas leņķi lēnām samazina līdz nullei (2. att.). Kad leņķis kļūst vienāds ar nulli, var redzēt, ka gaismas stars vairs neizkļūst no skaldnes AC. Leņķis BAC ir 40°.
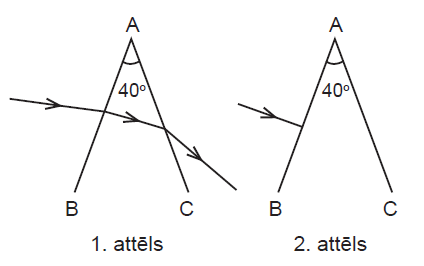
Aprēķini prizmas materiāla gaismas laušanas koeficientu! Parādi risinājuma gaitu! Iezīmē stara turpmāko gaitu 2. attēlā!
Uzdevumā ir aplūkota pilnīgās iekšējās atstarošanas parādība. Uzdevuma 2. attēlā, kur stars krīt perpendikulāri AB skaldnei, uz AC skaldnes notiek pilnīgā iekšējā atstarošanās.
Vispārīgajā gadījumā laušanas likuma formula: \(\frac{\sin{\alpha}}{\sin{\gamma}}=\frac{n_2}{n_1}\), kur \(\alpha\) – krišanas leņķis, \(\gamma\) – laušanas leņķis, \(n_1\) – pirmās vides gaismas laušanas koeficients, \(n_2\) – otrās vides gaismas laušanas koeficients. 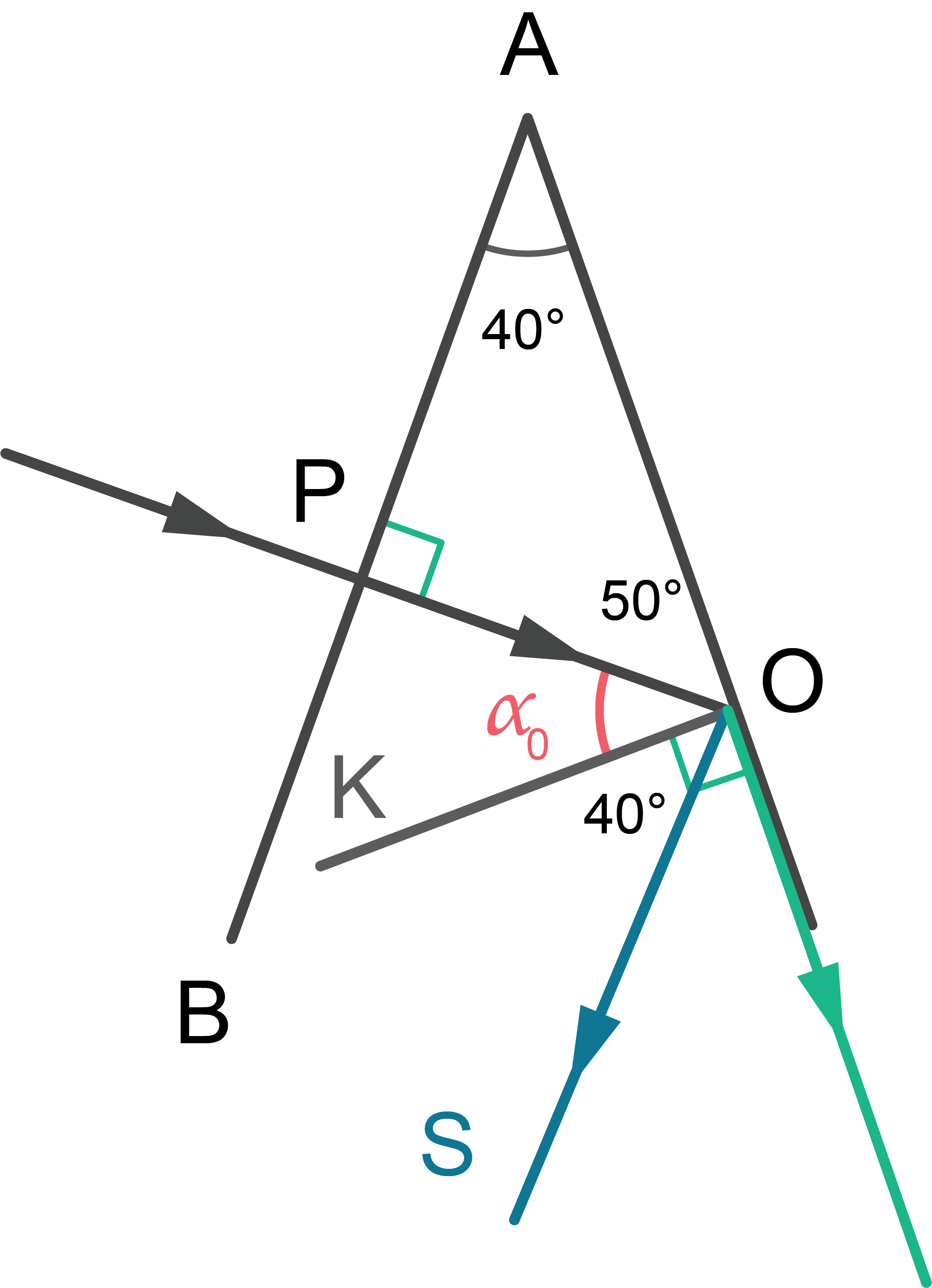
Pilnīgo iekšējo atstarošanos novēro, ja gaisma pāriet no vides ar lielāku laušanas koeficientu vidē ar mazāku laušanas koeficientu. Uzdevumā šāda situācija ir iespējama, ja gaismas stars iziet no prizmas gaisā.
Pilnīgās iekšējās atstarošanas robežleņķis \(\alpha_0\) (\(\angle\)POK) ir 40°. Taisnleņķa trijstūra leņķis \(\angle\)AOP ir 50°. Pilnīgās iekšējās atstarošanās robežleņķis \(\alpha_0\) summā ar leņķi \(\angle\)AOP veido 90°. Tātad pilnīgās iekšējās atstarošanas robežleņķis \(\alpha_0\)=40°.
Pilnīgās iekšējās atstarošanas robežleņķis \(\alpha_0\), kas uzdevumā ir vienāds 40o, ir krišanas leņķis, bet laušanas leņķis \(\gamma\) (attēlā \(\angle\)KOC) ir 90°. Formulā \(\frac{\sin{\alpha_0}}{\sin{\gamma}}=\frac{n_2}{n_1}\) pirmā vide ir prizmas materiāls, kura laušanas koeficients ir \(n_1\), ko apzīmē par \(n\). Otrā vide ir gaiss, kura laušanas koeficients ir \(n_2=1\).
Ievietojot skaitļus laušanas likuma formulā \(\frac{\sin{40^o}}{\sin{90^o}}=\frac{1}{n}\), iegūst, ka prizmas materiāla laušanas koeficients \(n\approx1,56\).
Stara PO turpmākā gaita parādīta attēlā. Punktā O var zīmēt vai atstaroto staru OS, vai lauzto staro, kas slīd gar AC skaldni.
Uzdevuma izpilde eksāmenā – 25,5%.
Vērtēšanas kritēriji
Turpina stara gaitu otrajā zīmējumā līdz skaldnei AC, attēlo perpendikulu krišanas punktā. Atzīmē zīmējumā krišanas leņķi \(\alpha_0\) uz skaldni AC. Aprēķina krišanas leņķa \(\alpha_0\) vērtību. Kopā – 1 punkts.
Aprēķina laušanas koeficientu –1 punkts.
Attēlo stara gaitu pēc atstarošanās no skaldnes AC vai slīdot pa to – 1 punkts.