Apmeklējot akvaparku, skolēns noslīdēja pa lielo cauruli, kas sākas 15 m augstumā virs baseina ūdens
līmeņa. Caurules garums ir 60 metri. Skolēns ūdens virsmu sasniedza ar 6 m/s lielu ātrumu. Ar aprēķiniem
pamato, vai noslīdēšanas laikā izmainījās skolēna pilnā mehāniskā enerģija! Aprēķinos pieņem, ka
\(g=10\space\mathrm{m/s^2}\) !
Skolēna masa ir 60 kg. Cik liels vidējais pretestības spēks darbojas uz skolēnu slīdēšanas laikā caurulē?
Ķermeņa pilnā mehāniskā enerģija \(W\) ir ķermeņa kinētiskās enerģijas \(W_\mathrm k\) un potenciālās enerģijas \(W_\mathrm p\) summa: \(W=W_\mathrm k+W_\mathrm p\). Par potenciālās enerģija nulles līmeni pieņem ūdens virsmu.
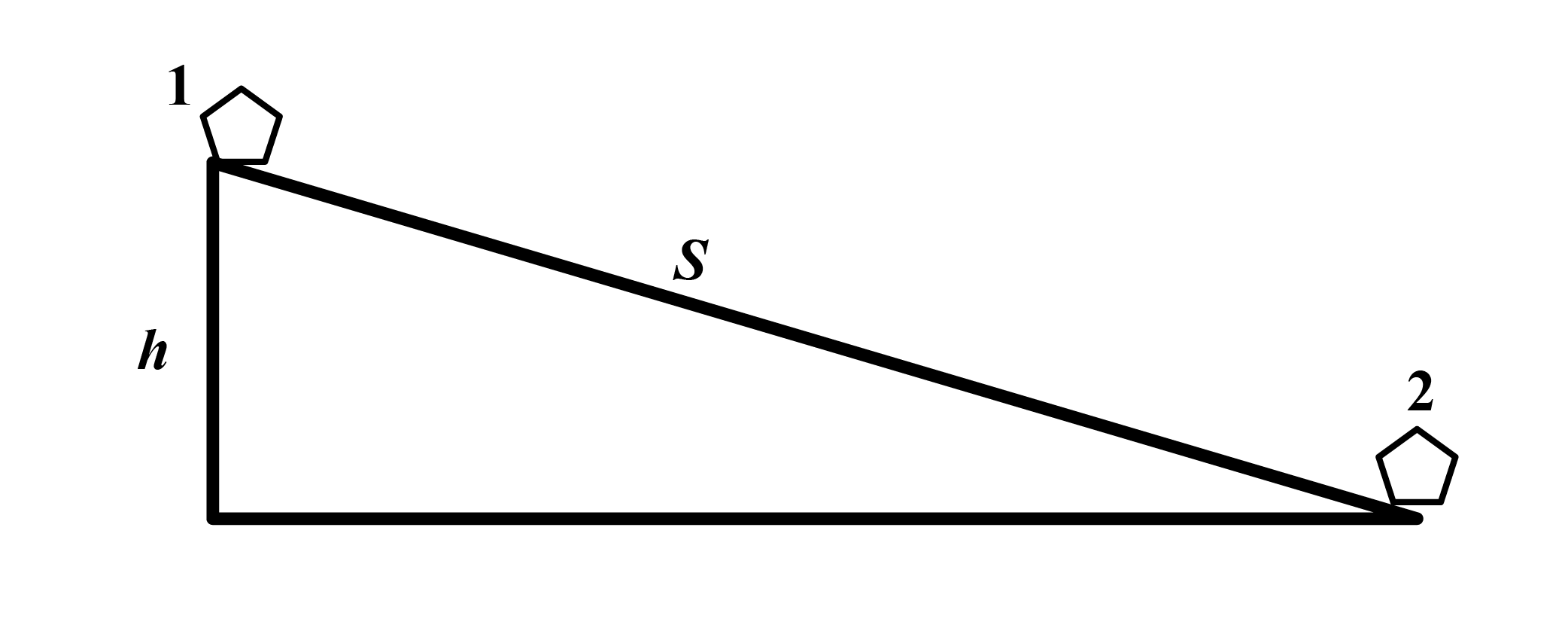
Kustības sākumā skolēns atrodas punktā 1. Ja skolēns sāk kustību no miera stāvokļa, tad punktā 1 pilnā mehāniska enerģija ir vienāda ar skolēna potenciālo enerģiju \(W_1=W_\mathrm {p1}=mgh\), kur \(m\) – skolēna masa, \(g\) – brīvās krišanas paātrinājums, \(h\) – augstums virs ūdens līmeņa. Pie ūdens virsmas punktā 2 pilnā mehāniskā enerģija ir vienāda ar skolēna kinētisko enerģiju \(W_2=W_\mathrm {k2}=\frac{mv^2}{2}\), kur \(v\) – skolēna ātrums punktā 2.
Var atbildēt uz eksāmena jautājumu, ja skolēna masa nav zināma:
\(W_1=mgh=m\cdot10\cdot15 =150\cdot m\space\mathrm J\).
\(W_2=\frac{mv^2}{2}=\frac{m\cdot6^2}{2}=18\cdot m\space\mathrm J\).
\(150\cdot m\space\mathrm J>18\cdot m\space\mathrm J\) – noslīdēšanas laikā skolēna pilnā mehāniskā enerģija izmainījās, tā samazinājās.
Var izmantot skolēna masu \(m=60\space\mathrm{kg}\) no uzdevuma otrās daļas:
\(W_1=mgh=60\cdot10\cdot15=9000\space\mathrm J\).
\(W_2=\frac{mv^2}{2}=\frac{60\cdot6^2}{2}=1080\space\mathrm J\).
\(9000\space\mathrm J>1080\space\mathrm J\) – noslīdēšanas laikā skolēna pilnā mehāniskā enerģija izmainījās, tā samazinājās.
Skolēna pilnā mehāniskā enerģija samazinājās par \(\Delta W=W_1-W_2=mgh-\frac{mv^2}{2}=9000-1080=7920\space\mathrm J\). Tik liels darbs \(A\) ir veikts pretestības spēku pārvarēšanai. Mehāniskā darba \(A\) formula \(A=Fs\), kur \(F\) – vidējais pretestības spēks, \(s\) – skolēna pārvietojuma modulis. Tālāk nosaka vidējo pretestības spēku \(F=\frac{A}{s}\).
Aprēķini:
\(W_1=mgh=60\cdot10\cdot15=9000\space\mathrm J\).
\(W_2=\frac{mv^2}{2}=\frac{60\cdot6^2}{2}=1080\space\mathrm J\).
\(A=\Delta W=W_1-W_2=9000-1080=7920\space\mathrm J\)
\(F=\frac{A}{s}=\frac{7920}{60}=132\space\mathrm N \approx130\space\mathrm N\).
Atbilde: noslīdēšanas laikā izmainījās skolēna pilnā mehāniskā enerģija izmainījās. Vidējais pretestības spēks ir \(130\space\mathrm N\).
Vērtēšanas kritēriji
Aprēķina skolēna potenciālo un pilno mehānisko enerģiju augstākajā caurules punktā – 1 punkts.
Aprēķina skolēna kinētisko un pilno mehānisko enerģiju zemākajā caurules punktā. Salīdzina pilno mehānisko enerģiju augstākajā un zemākajā caurules punktā. Izdara secinājumu par pilnās enerģijas maiņu – 1 punkts.
Zina, kā aprēķina mehānisko darbu, un aprēķina vidējo pretestības spēku – 1 punkts.