Skolēns noliktavā atrada vara stieples spoli, izmērīja stieples elektrisko pretestību un vara masu spolē.
Iegūtie rezultāti: \(27~\Omega\) un \(0,25~\mathrm{kg}\). Vara blīvums \(\rho_\mathrm{b}=8,9\cdot10^3~\mathrm{kg/m^3}\), un tā īpatnējā pretestība \(\rho_\mathrm{p}=1,68\cdot10^{-8}~\Omega\cdot\mathrm{m}\).
1. Aprēķini, cik metru stieples ir izmantots vienas spoles uztīšanai! (3 punkti)
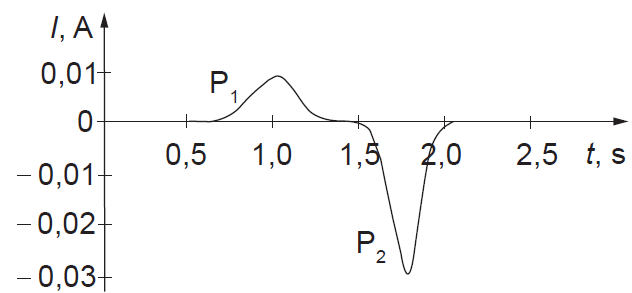2. Skolēns pētīja spoli ar tai pievienotu jutīgu galvanometru, pārvietojot pastāvīgo magnētu tuvāk un tālāk no spoles. Grafikā redzamas strāvas izmaiņas spolē: impulss P1 (pīķis) – magnētam virzoties tuvāk spolei, impulss P2 – magnētam attālinoties no spoles.
Paskaidro, kāpēc, magnētu attālinot no spoles, tas pārvietojas ātrāk nekā gadījumā, kad to tuvina spolei! (3 punkti)
3. Paskaidro, kas notiktu, ja skolēns samainītu vietām magnēta polus (ziemeļu ar dienvidu) un saglabātu tādu pašu magnēta tuvināšanas un attālināšanas ātrumu! (2 punkti)
4. Trīskāršojot elektriskās strāvas stiprumu spolē, kuras induktivitāte ir \(0,25~\mathrm{H}\), spoles magnētiskā lauka enerģija palielinās par \(1~\mathrm{J}.\) Aprēķini elektriskās strāvas stipruma sākotnējo vērtību! (2 punkti)
1. Risinājumā jāizmanto datu bukletā atrodamās pretestības formula \(R=\frac{\rho_\mathrm{p}l}{S}\) un sakarība starp ķermeņa masu, blīvumu un tilpumu. Tilpums \(V\) jāizsaka kā vada garuma \(l\) un šķērsgriezuma laukuma \(S\) reizinājums \(V=S\cdot l\).
\(\)\(\rho_\mathrm{b}=\frac{m}{V}=\frac{m}{Sl}\) \(\implies\) \(S=\frac{m}{\rho_\mathrm{b}l}\).
Ievietojot iegūto izteiksmi pretestības formulā: \(R=\frac{\rho_\mathrm{p}l}{S}=\frac{\rho_\mathrm{p}l{\rho_\mathrm{b}}l}{m}=\frac{\rho_\mathrm{p}{\rho_\mathrm{b}}l^2}{m}\). Izsakot vada garumu, iegūst \(l=\sqrt{\frac{mR}{\rho_\mathrm{p}\rho_\mathrm{b}}}=\sqrt{\frac{0,25\cdot27}{1,68\cdot10^{-8}\cdot8,9\cdot10^3}}\approx213\space\mathrm{m}\).
Cits risinājuma variants ir izmantot sistēmu no diviem vienādojumiem:
\(\begin{cases} R=\frac{\rho_\mathrm{p}l}{S}\\ m=\rho_\mathrm{b}lS \end{cases}\)
abu vienādojumu kreisās un labās puses sareizina: \(Rm=\rho_\mathrm{p}\rho_\mathrm{b}\frac{l}{S}lS=\rho_\mathrm{p}\rho_\mathrm{b}L^2\). Izsakot vada garumu, iegūst \(l=\sqrt{\frac{mR}{\rho_\mathrm{p}\rho_\mathrm{b}}}=\sqrt{\frac{0,25\cdot27}{1,68\cdot10^{-8}\cdot8,9\cdot10^3}}\approx213\space\mathrm{m}\).
Atbilde: vienas spoles uztīšanai izmantots aptuveni \(213\space\mathrm{m}\) garš vads.
2. Šajā uzdevumā, acīmredzot, jāpaskaidro elektromagnētiskās indukcijas strāvas stipruma saistība ar magnēta kustības ātrumu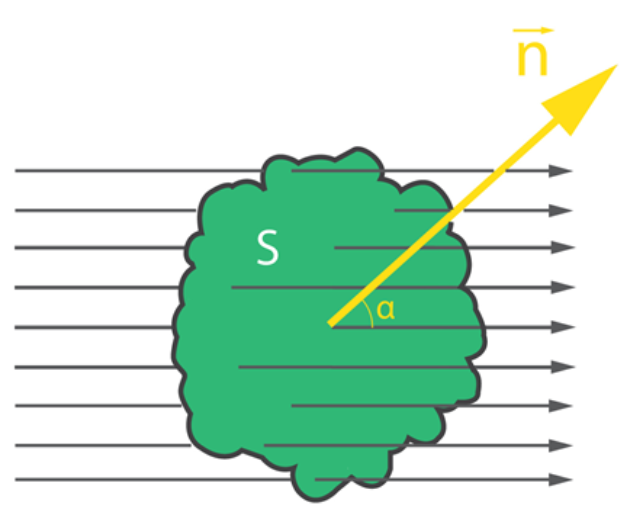
spoli tuvinot un attālinot. Tomēr jautājumu var saprast arī tā: jāpaskaidro cēloni tam, ka magnētu attālina ātrāk nekā to tuvina spolei. Tā kā uzdevumā dots grafiks, tad, skaidrojot šos cēloņus, ir jāpiemin elektromagnētiskās indukcijas strāvas stipruma saistība ar magnēta kustības ātrumu. Lai atbildētu, jāzina Faradeja likums: mainoties magnētiskā lauka plūsmai \(\Phi=BS\cos{\alpha}\), tajā rodas (inducējas) elektrodzinējspēks \(\mathscr{E}=-N\frac{\Delta\Phi}{\Delta t}\)(šīs sakarības atrodamas datu bukletā). Tad, saskaņā ar Oma likumu, spolē inducētās strāvas stiprumu var aprēķināt \(I=-\frac{\Delta\Phi}{R\Delta t}\).
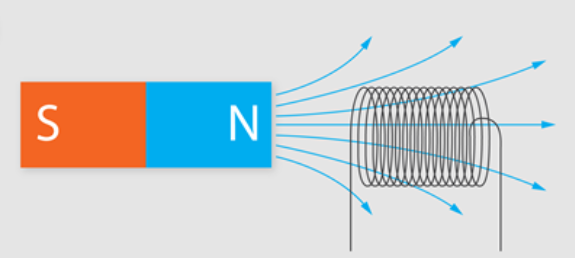Panākt, ka magnētiskā lauka plūsma caur vadītāja kontūru mainās, var tuvinot vai attālinot stieņveida pastāvīgo magnētu spolei (jo tuvāk magnēta polam, jo tā magnētiskais lauks stiprāks).
Tuvinot magnētu ar lielāku ātrumu, magnētiskā lauka plūsmas izmaiņa laika vienībā būs lielāka, tātad – lielāks būs arī strāvas stiprums. Tā kā impulsa P2 strāvas stipruma maksimālā vērtība ir lielāka nekā impulsam P1, magnēts attālināts ar lielāku ātrumu, nekā tas tuvināts.
Turklāt no grafika redzams arī, ka tuvināšana notika divas reizes ilgāk (1 s) nekā attālināšana (0,5 s). Ja pieņem, ka attālumi vienādi, skaidrs, ka attālināšana notika divas reizes ātrāk.
Par elektromagnētisko indukciju vairāk lasi "Fiztēmās": https://www.fizmix.lv/fiztemas/elektromagnetisms-11/elektromagnetiska-indukcija
3. Lai atbildētu, jāzina Lenca likums – ko nozīmē mīnusa zīme datu bukletā atrodamajā sakarībā \(\mathscr{E}=-N\frac{\Delta\Phi}{\Delta t}\).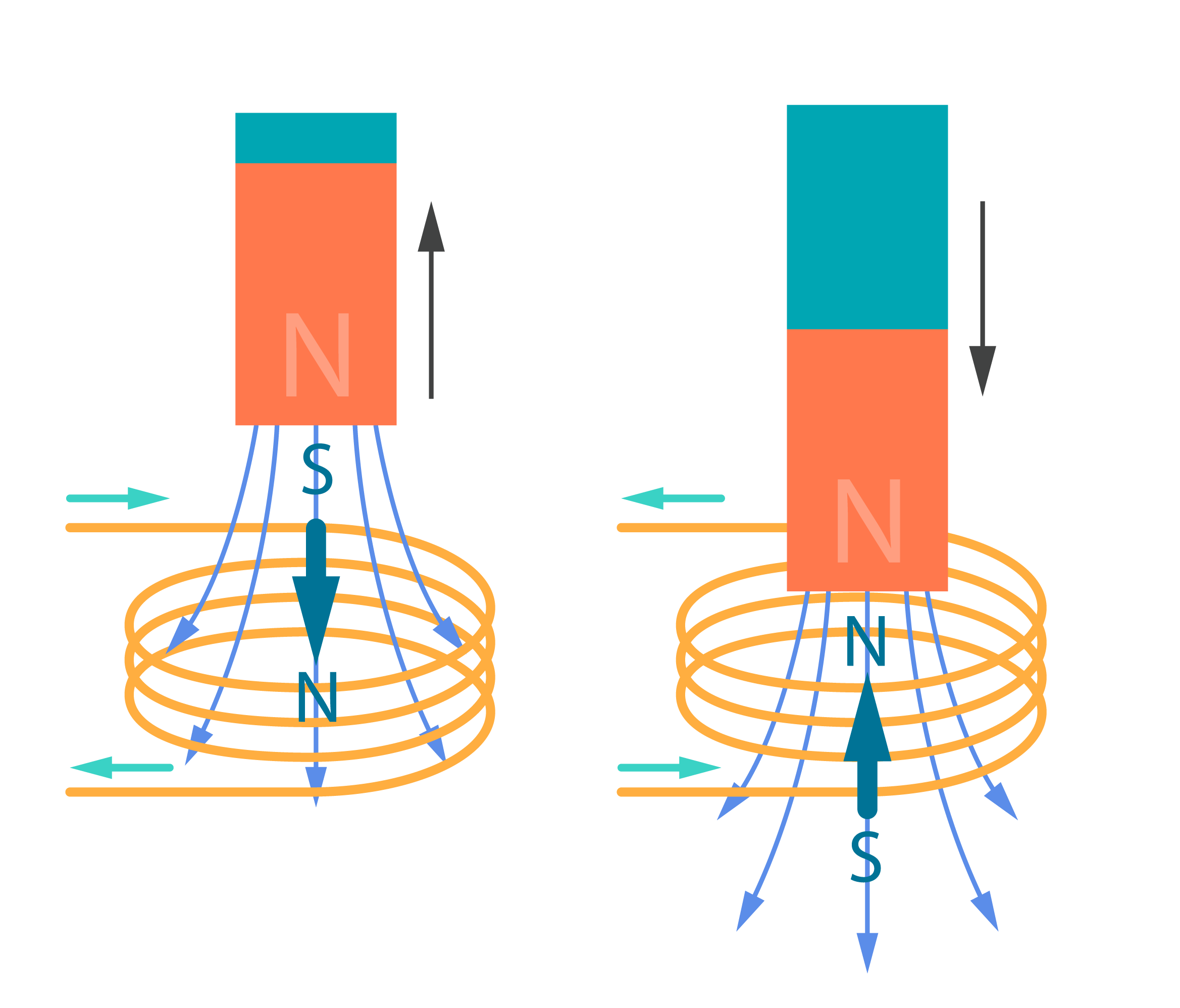 
Tas nozīmē, ka inducētā strāva vienmēr rodas tādā virzienā, lai ''pretdarbotos'' magnētiskās plūsmas izmaiņai kontūrā. Šīs strāvas radītais magnētiskais lauks būs vērst tā, lai mazinātu notiekošās izmaiņas. Tuvinot magnētu magnētiskā plūsma caur spoles vijumiem pieaug, tātad inducētā strāva būs vēsta tā, lai šīs strāvas radītais magnētiskais lauks būtu vērsts pretēji stieņveida magnēta magnētiskajam laukam. Savukārt, magnātu attālinot, inducētās strāvas magnētiskais lauks vērsts tāpat kā stieņveida magnēta lauks.
Šo parādību var aplūkot arī no enerģijas nezūdamības likuma viedokļa – faktiski elektriskās strāvas enerģijā ir pārvērsts mehāniskais darbs, tuvinot magnētu, kas padarīts, pārvarot uzradušos pretestības spēku tā tuvināšanai.... ja spole magnētu ievilktu, nevis pretotos, rastos ''mūžīgais dzinējs''. Var uz to lūkoties arī kā uz III Ņūtona likuma izpausmi – katrai iedarbībai ir pretdarbība. Var aplūkot arī tā: kas liek lādiņnesējiem kustēties? Tas ir Lorenca spēks, kas darbojas uz lādētu daļiņu magnētiskajā laukā – ja pārvietojama vadu, pārvietojam arī lādiņnesējus tajā... uz tiem darbojas Lorenca spēks un liek virzīti kustēties.
Par elektromagnētisko indukciju vairāk lasi "Fiztēmās": https://www.fizmix.lv/fiztemas/elektromagnetisms-11/elektromagnetiska-indukcija
Atbilde
Mainās magnētiskā lauka un tā izmaiņas virziens. Līdz ar to mainās strāvas virziens spolē tuvinot un attālinot magnētu. Tā kā tuvināšanas un attālināšanas ātrumi nemainās, strāvas stipruma absolūtās vērtības barī nemainās.
4. Jāzina vai jāatrod datu bukletā sakarība, kas saista spoles magnētiskā lauka enerģiju ar strāvas stiprumu tajā: \(W=\frac{LI^2}{2}\).
Izmantojot šo sakarību, var izteikt magnētiskā lauka enerģijas izmaiņu ar elektriskās strāvas stipruma sākotnējo vērtību \(I\):
\(\Delta W=\frac{L\cdot (3I)^2}{2}-\frac{L\cdot I^2}{2}=\frac{8LI^2}{2}=4LI^2\). Izsakot strāvas stiprumu, iegūst: \(I=\sqrt{\frac{\Delta W}{4L}}=\sqrt{\frac{1}{4\cdot0,25}}=1\space\mathrm{A}\).
Atbilde: elektriskās strāvas stipruma sākotnējā vērtība \(I=1\space\mathrm{A}\).
1. Vērtēšanas kritēriji
• Izmanto pretestības un blīvuma formulas (formulas un/vai formulās ievietoti skaitļi) – 1 punkts.
• Saista vada tilpumu ar tā garumu un šķērsgriezuma laukumu. Izsaka vada garumu – 1 punkts.
• Aprēķina vada garumu skaitliski, norāda mērvienību – 1 punkts.
Ja skolēns izvēlējies risinājuma veidu, kas nav aprakstīts kritērijos, vērtētājs patstāvīgi sadala risinājumu soļos, atbilstoši dotajam punktu skaitam. Pieļaujama viena nebūtiska kļūda skaitliskajā aprēķinā. Zīmīgo ciparu skaitu nevērtē. Punktu par skaitlisku aprēķinu ieskaita arī tad, ja pieļauta kļūda, izsakot vada garumu no pareizi uzrakstītām formulām (risinājumā parādās visas trīs nepieciešamās formulas, bet otro punktu ieskaitīt nevar).
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
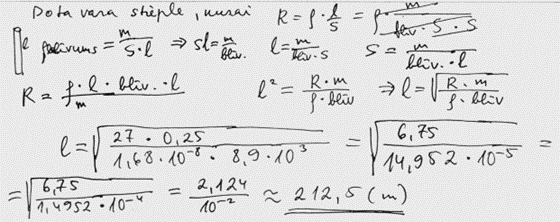
2. piemērs: risinājums novērtēts ar 3 punktiem.
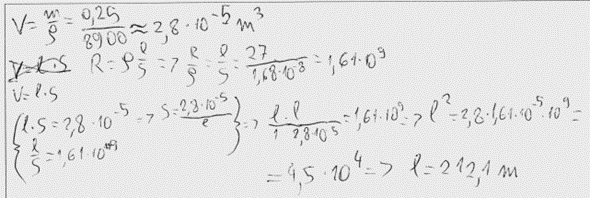
3. piemērs: risinājums novērtēts ar 2 punktiem. Kaut kur pazuda blīvums, bet sākumā bija. Neieskaita 2. punktu.
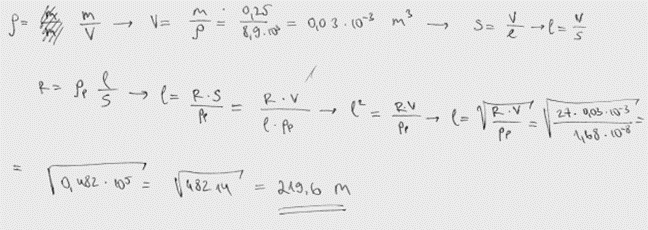
4. piemērs: risinājums novērtēts ar 1 punktu. Risinājumā atspoguļots tikai pirmais punkts no vērtēšanas kritērijiem.
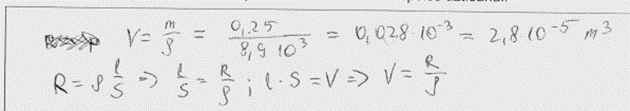
5. piemērs: risinājums novērtēts ar 0 punktu.
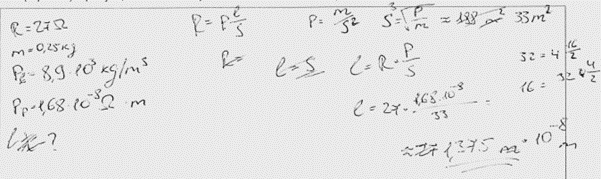
2. Vērtēšanas kritēriji
Vērtē līmeņos
3 punkti
Saista indukcijas EDS un inducētās strāvas stiprumu ar magnētiskās plūsmas izmaiņas ātrumu (Faradeja likums).
VAI
Skaidro, kādēļ magnētu tuvināt ir grūtāk, nekā to attālināt UN ir pieminēta strāvas virziena un maksimālās vērtības saistība ar magnēta pārvietošanas ātrumu un virzienu.
2 punkti
Saista indukcijas EDS vai inducētās strāvas stiprumu ar magnētiskās plūsmas izmaiņas ātrumu.
VAI
Piemin vienu būtisku aspektu saistot magnēta kustību ar elektromagnētiskās indukcijas EDS vai strāvu UN uzrakstīta, ka magnētu tuvināt ir grūtāk, nekā attālināt bez pieņemama pamatojuma.
1 punkts
Piemin vienu būtisku aspektu saistot magnēta kustību ar elektromagnētiskās indukcijas EDS vai strāvu
VAI
Uzraksta, ka magnētu tuvināt ir grūtāk, nekā attālināt, bez pieņemama pamatojuma.
0 punktu, ja pamatojuma nav vai tikai aplami spriedumi.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 2 punktiem.
4. piemērs: risinājums novērtēts ar 1 punktu. Mēģinājums skaidrot, kādēļ tuvināt ir grūtāk.
5. piemērs: risinājums novērtēts ar 1 punktu. Salīdzināti laika intervāli tuvinot un attālinot, bet – nav atbildes uz jautājumu.
6. piemērs: risinājums novērtēts ar 0 punktu.
3. Vērtēšanas kritēriji
• Spriež par strāvas virziena maiņu – 1 punkts.
• Spriež, ka strāvas stipruma absolūtās vērtības atkarība no laika nemainās – 1 punkts.
Atbilde var būt uzzīmēts grafiks.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
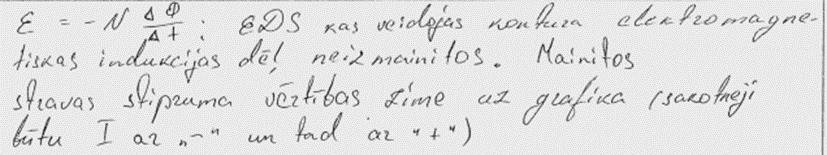
3. piemērs: risinājums novērtēts ar 2 punktiem.
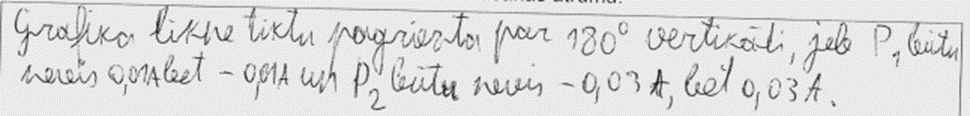
4. piemērs: risinājums novērtēts ar 1 punktu. Netiek pieminēts, ka ka strāvas stipruma modulis atkarība no laika nemainās.
5. piemērs: risinājums novērtēts ar 0 punktu. Atbilde būtībā atkārto uzdevuma tekstu.
6. piemērs: risinājums novērtēts ar 0 punktu. Nav saprotams – kas un kam "pretējais".
4. Vērtēšanas kritēriji
• Uzraksta sakarību magnētiskā lauka enerģijas izmaiņas aprēķināšanai – 1 punkts.
• Izsaka no formulas un aprēķina sākotnējo strāvas stiprumu, norādot mērvienību – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
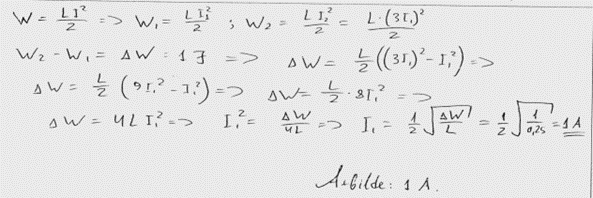
2. piemērs: risinājums novērtēts ar 1 punktu. Tipiska matemātiska kļūda.
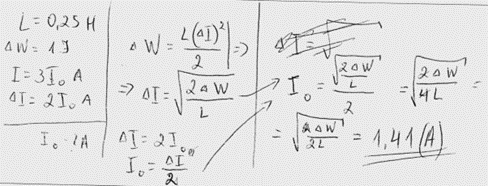
3. piemērs: risinājums novērtēts ar 0 punktu.
