Neliela lidmašīna lido paralēli Zemes virsmai ar ātrumu \(150\space\mathrm{m/s}\). Magnētiskais lauks ir vērsts \(70^{\mathrm{o}}\) lielā leņķī attiecībā pret Zemes virsmu, un tā indukcija ir \(48\space\mathrm{\mu T}\) (sk. zīmējumu). Attālums starp lidmašīnas spārnu galiem \(L=30\space\mathrm{m}\).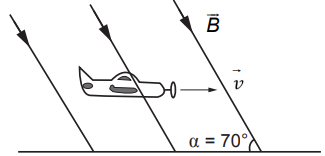
Aprēķini, cik liels spriegums inducēsies starp lidmašīnas spārnu galiem! Parādi risinājuma gaitu!
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Kustībā esošos vadītajos magnētiskajā laukā indukcijas EDS \(\mathscr{E}_\mathrm i\) nosaka pēc formulas \(\mathscr{E}_\mathrm i=Blv\sin\alpha\), kur \(B\) – magnētiskā lauka indukcija, \(l\) – vadītāja garums, \(v\) – vadītāja kustības ātrums attiecībā pret magnētisko lauku, \(\alpha\) – leņķis starp ātruma un magnētiskās indukcijas vektoriem. Uzdevumā vadītāja vietā ir lidmašīnas spārni ar attālumu starp galiem \(L\). Indukcijas EDS jāaprēķina starp lidmašīnas spārnu galiem, tādēļ \(L=l\).
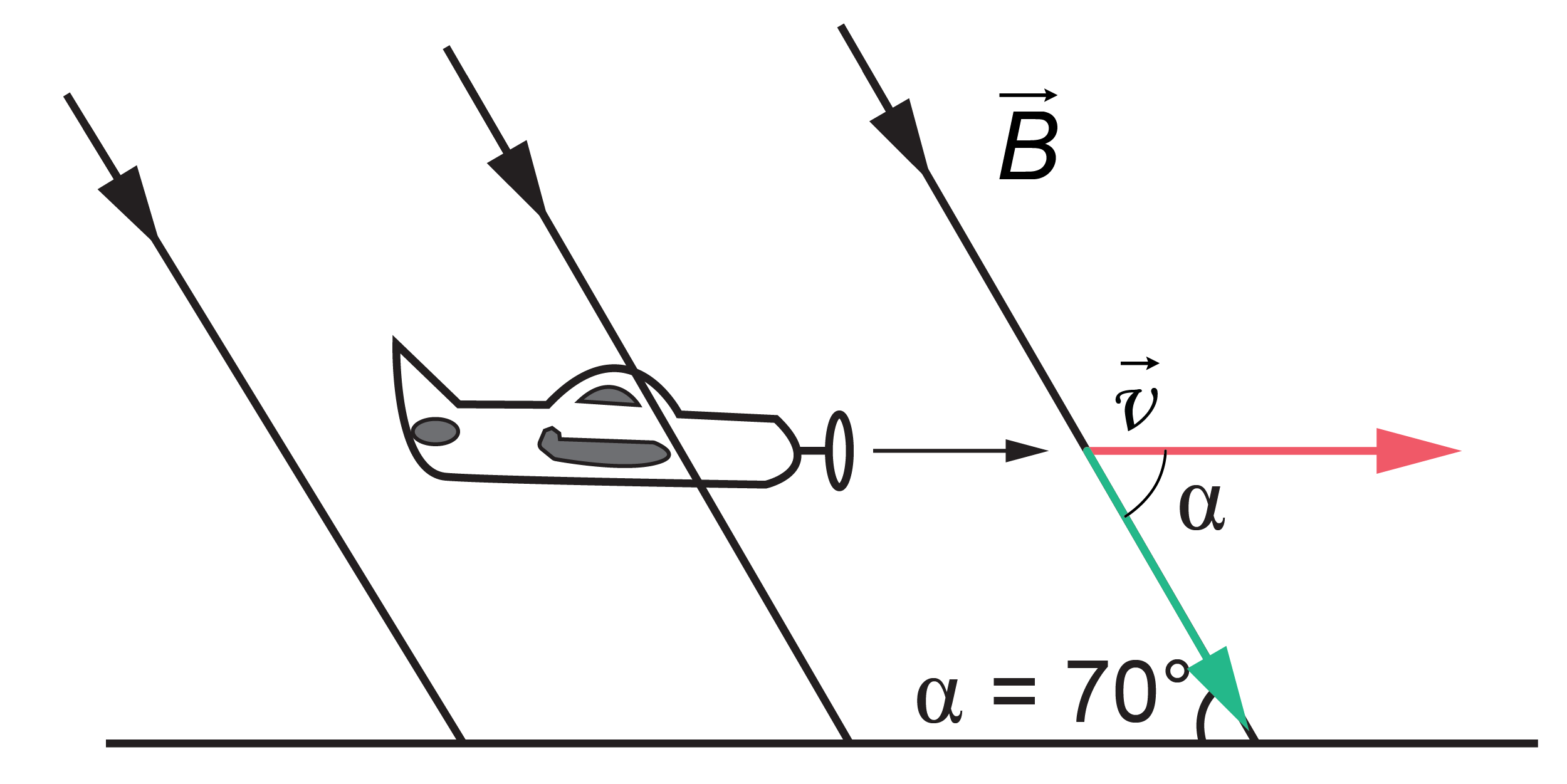
Leņķi \(\alpha\), kurš dots uzdevumā (skatīt attēlu), veido magnētiskā lauka indukcijas līnijas un Zemes virsma. Taču tas ir skaitliski vienāds ar citu leņķi \(\alpha\), ko veido ātruma vektors (sarkanais vektors attēlā) un magnētiskās indukcijas vektors (zaļais vektors attēlā). Matemātikā tādus leņķus, kas veidojas divām paralēlām taisnēm šķērsojot trešo taisni, sauc par iekšējiem šķērsleņķiem.
Aprēķini
\(\mathscr{E}_\mathrm i=BLv\sin\alpha=48\cdot 10^{-6}\cdot30\cdot150\cdot\sin70^{\mathrm o}\approx20\space\mathrm V\)
Atbilde: inducētais spriegums starp lidmašīnas spārnu galiem ir aptuveni \(0,20\space\mathrm V\).
Uzdevuma izpilde eksāmenā - 39,2%.
Vērtēšanas kritēriji
Zina vai atrod formulu lapā atbilstošo formulu – 1 punkts.
Saskaņo fizikālo lielumu mērvienības – 1 punkts.
Aprēķina indukcijas EDS vērtību, noapaļo rezultātu un pieraksta mērvienības – 1 punkts.