Ja punktveida lādiņš ir pozitīvs, tad elektriskā lauka intensitātes vektors ir vērsts prom no lādiņa.
Lādiņa Q veidotā elektriskā lauka intensitātes vektora moduli nosaka pēc formulas E=k|Q|R2, kur k – Kulona likuma konstante, R – attālums starp lādiņu un telpas punktu.
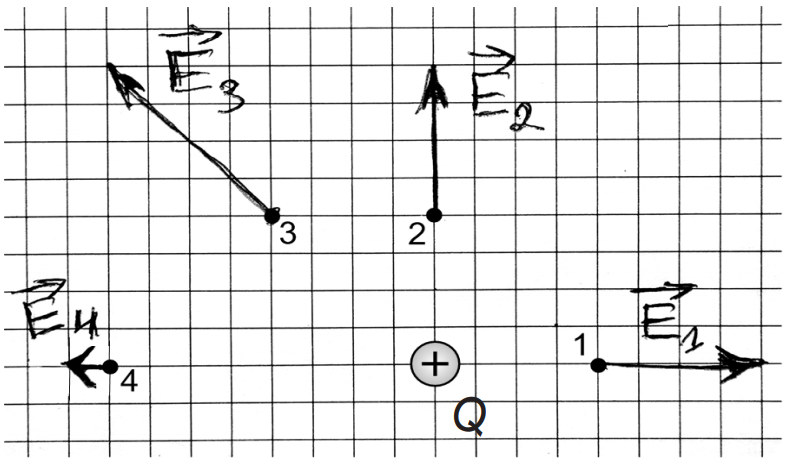
Visi četri vektori vērsti prom no lādiņa Q. Tādēļ teorētiski vektori var būt attēloti pareizi. Nepieciešams salīdzināt vektoru moduļus.
Vektoru moduļus uzdevumā izmēra nosacītās vienībās – rūtiņās. Attālumus un vektora moduļus var izmērīt arī ar lineālu.
Attēlā katram elektriskā lauka intensitātes vektoram attēloti moduļi un attālumi līdz lādiņam Q, kas rada elektrisko lauku.
Saskaņā ar uzdevuma tekstu vektors →E1 ir attēlots pareizi. Vektors →E2 pēc moduļa (bultiņas garuma attēlā) vienāds ar vektoru →E1. Punkti 1 un 2 atrodas vienādos attālumos no lādiņa Q. Var secināt, ka vektors →E2 attēlots pareizi.
Punkts 3 atrodas no lādiņa Q tālāk nekā punkts 1, bet vektora →E3 modulis (bultiņas garums attēlā) ir lielāks nekā vektora →E1 modulis. Saskaņā ar formulu E=k|Q|R2, ir jābūt otrādi – lielākā attālumā no lādiņa elektriskā lauka intensitāte ir mazāka. Tādēļ var secināt, ka vektors →E3 ir attēlots nepareizi.
Attālums starp lādiņu Q un punktu 4 ir 8 rūtiņas jeb divas reizes lielāks, nekā attālums starp lādiņu Q un punktu 1. Vektora →E4 modulis ir vienāds ar vienu rūtiņu jeb vienu nosacīto vienību. Tātad vektora →E4 modulis ir četras reizes mazāks nekā vektora →E1 modulis. Saskaņā ar formulu E=k|Q|R2 viss ir pareizi – attālums pieaug divas reizes, saucējā attālums kvadrātā pieaug četras reizes, bet vektora modulis samazinās četras reizes. Tādēļ vektors →E4 arī ir attēlots pareizi.
Atbilde: Vektori →E2 un →E4 attēloti pareizi, vektors →E3 attēlots nepareizi.