Trīs mazas metāla lodītes ir nostiprinātas nekustīgi vakuumā. Visu lodīšu lādiņš ir vienāds.
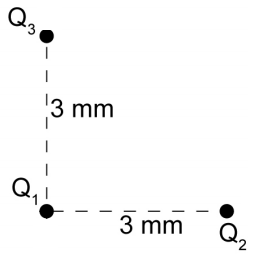
Attēlo zīmējumā elektrostatiskos spēkus, ar kādiem lodītes Q2 un Q3 iedarbojas uz lodīti Q1, un rezultējošo spēku! Parādi spriedumu gaitu!
Visām trim lodītēm ir vienāds lādiņš, kas nozīmē gan vienādas lādiņu zīmes, gan vienādas lādiņa skaitliskās vērtības. Tāpēc risinājumā var situāciju modelēt vai nu ar visiem pozitīviem lādiņiem, vai visiem negatīviem. Tā kā visu lādiņu zīmes ir vienādas, starp metāla lodītēm darbojas tikai atgrūšanās spēki, un atbilde abos gadījumos ir vienāda.
Elektrostatiskā spēka jeb lādiņu mijiedarbības spēka moduli \(F\) starp punktveida lādētiem ķermeņiem nosaka pēc Kulona likuma:
\(F=k\frac{\mid Q_1 \mid Q_2 \mid}{R^2}\), kur \(k\) - Kulona likuma konstante, \(Q_1\) un \(Q_2\) - ķermeņu elektriskie lādiņi, \(R\) - attālums starp lādētajiem ķermeņiem.
Attālums starp pirmo un otro lodīti ir tāds pats, kā attālums starp pirmo un trešo lodīti. Tādēļ mijiedarbības spēki, ar kādiem otrā un trešā lodīte darbojas uz pirmo lodīti, ir vienādi pēc moduļa.
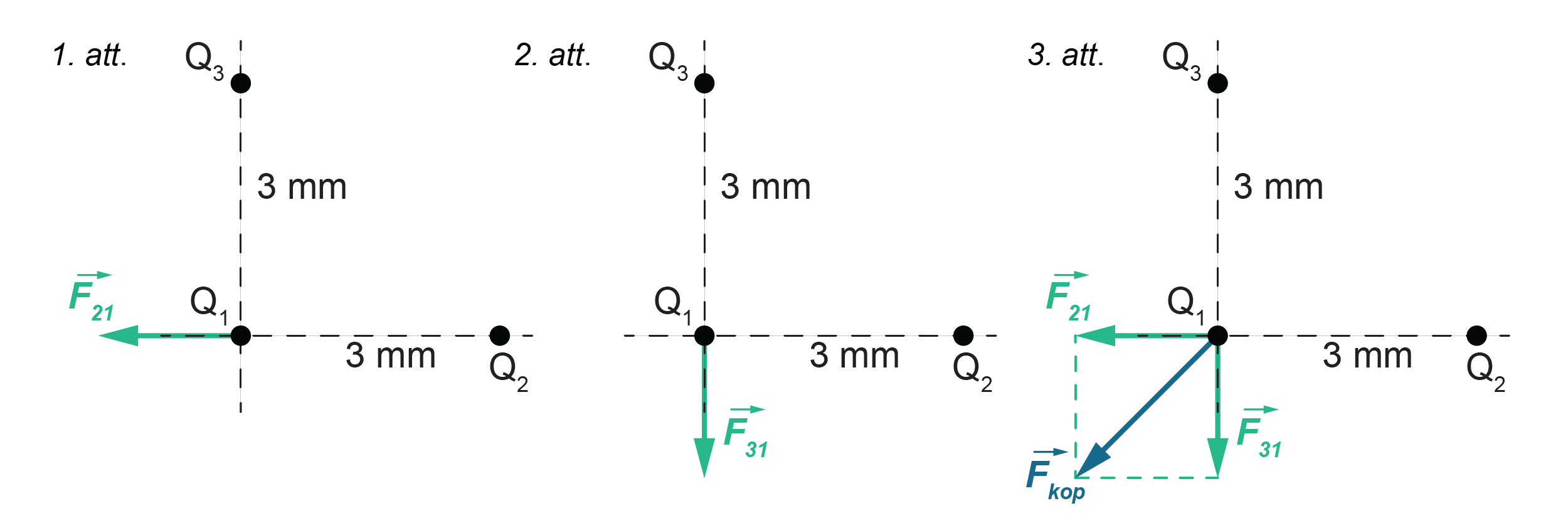
Risinājumā attēlo elektostatisko spēku \(\overrightarrow{F}_{21}\), ar kādu otrā lodīte darbojas uz pirmo lodīti un elektostatisko spēku \(\overrightarrow{F}_{31}\), ar kādu trešā lodīte darbojas uz pirmo lodīti. Lai iegūtu rezultējošo spēku jeb kopspēku \(\overrightarrow{F}_{\mathrm{kop}}\), spēki \(\overrightarrow{F}_{21}\) un \(\overrightarrow{F}_{31}\) ir vektoriāli jāsaskaita (skatīt attēlu). Vektorus saskaita, konstruējot paralelogramu, šajā gadījumā kvadrātu. Paralelograma jeb kvadrāta diagonāle ir rezultējošā spēka jeb kopspēka vektors.
Vērtēšanas kritēriji
Zina, ka, ja lādiņu zīmes ir vienādas, darbojas atgrūšanās spēks. Attēlo zīmējumā atgrūšanās spēkus un pieraksta to apzīmējumus – 1 punkts.
Zina, ka, ja lādiņu moduļi ir vienādi, tad mijiedarbības spēki arī ir vienādi. Attēlo zīmējumā pēc moduļa vienādus spēkus – 1 punkts.
Attēlo rezultējošo spēku jeb kopspēku, pieraksta to apzīmējumu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemērī
1. piemērs: risinājums novērtēts ar 3 punktiem.

2. piemērs: risinājums novērtēts ar 2 punktiem (uzdevuma skaidrojumā nekas nav pateikts par rezultējošo spēku, zīmējumā nav parādīts, ka spēks ir vektoriāls lielums).

3. piemērs: risinājums novērtēts ar 1 punktu.

4. piemērs: risinājums novērtēts ar 0 punktiem.

5. piemērs: risinājums novērtēts ar 0 punktiem.

6. piemērs: risinājums novērtēts ar 0 punktiem.
