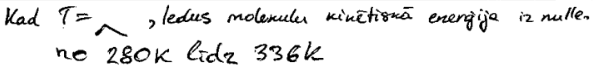Sildītāju, kura jauda ir \(150~\mathrm{W}\), izmanto, lai uzsildītu \(25~\mathrm{g}\) ledus noslēgtā un labi izolētā traukā. Sākotnējā ledus temperatūra ir \(-20~\mathrm{^\mathrm{o}C}\).
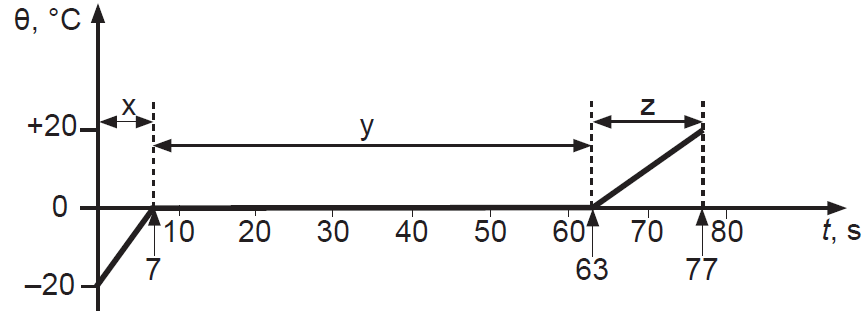
Grafiks parāda temperatūru \(\mathrm{\Theta}\) atkarībā no laika \(t\), skaitot no ledus sildīšanas sākuma.
1. Aprēķini ledus īpatnējo siltumietilpību, izmantojot grafiku! (3 punkti)
2. Kurā posmā ledus kūst? Cik ilgi ledus kūst? (1 punkts)
3. Izmantojot grafiku, salīdzini ledus un ūdens īpatnējo siltumietilpību! Argumentē savu atbildi! (3 punkti)
4. Grafikā ir trīs atšķirīgi reģioni/posmi: x, y un z. Raksturo molekulu kustību reģionā x un reģionā z! (1 punkts)
5. Ledus iekšējā enerģija palielinās no ledus sildīšanas sākuma, kad \(\mathrm{t=0}\), līdz laika momentam \(t=77~\mathrm{s}\). Aizpildi zemāk esošo tabulu, izmantojot šādu fizikālo lielumu apzīmējumus: K – iekšējā kinētiskā enerģija; P – iekšējā potenciālā enerģija! (1 punkts)

6. Kādā temperatūrā ledus molekulu kinētiskā enerģija ir nulle? (1 punkts)
1.  Ledus silst grafika pirmajā (x) posmā. Ledus silst 7 sekundes un šajā lākā tā temperatūra pieaug par \(\Delta\mathrm{\Theta}=20\mathrm{\space^oC}\).
Ledus silst grafika pirmajā (x) posmā. Ledus silst 7 sekundes un šajā lākā tā temperatūra pieaug par \(\Delta\mathrm{\Theta}=20\mathrm{\space^oC}\).
Zinot sildītāja jaudu (\(P=150\space\mathrm{W}\)), var aprēķināt tā izdalīto siltuma daudzumu \(Q\). Jāpieņem, ka sildītāja lietderības koeficients ir \(100\%\).
\(P=\frac{Q}{t}\space\implies\space Q=Pt=150\cdot7=1050\space\mathrm{J}\)
Zinot pievadīto siltuma daudzumu \(Q\), ledus masu \(m\) un temperatūras izmaiņu \(\Delta\mathrm{\Theta}\), aprēķina ledus īpatnējo siltumietilpību \(c\):
\(Q=cm\Delta\mathrm{\Theta}\space\implies\space c=\frac{Q}{m\Delta\mathrm{\Theta}}=\frac{1050}{0,025\cdot20}=2100\space\mathrm{\frac{J}{kg\cdot K}}\)
Atbilde: ledus īpatnējā siltumietilpība \(c=2100\space\mathrm{\frac{J}{kg\cdot K}}\)
2. Kristāliskai vielai (ledum) kūstot, tās temperatūra nemainās – vienkāršoti sakot, visa vielai pievadītā enerģija tiek tērēta starpmolekulāro saišu saraušanai. Kušana notiek katrai vielai raksturīgā kušanas temperatūrā. Kā zināms – vienas atmosfēras spiedienā ledus kūst \(0\space\mathrm{^oC}\) temperatūrā. Tam atbilst posms (reģions) y. Kušanas ilgums \(t=63-7=56\space\mathrm{s}\).
Atbilde: posms y, kušanas ilgums \(56\) sekundes.
3. Ledus silst posmā x, kas ilgst 7 sekundes. Savukārt ūdens, pēc tam, kad ledus pilnībā izkusis, sasilst par tādu pašu \(\Delta\mathrm{\Theta}=20\mathrm{\space^oC}\) divas reizes ilgākā laikā jeb 14 sekundēs (posms z). Jāpieņem, ka sildītāja jauda nav mainījusies, tātad ūdens silstot saņēmis divas reizes lielāku siltuma daudzumu \(Q\). Jāpieņem arī, ka ledus masa izkūstot nav mainījusies. Tātad, ūdenim īpatnējā siltumietilpība ir divas reizes lielāka nekā ledum.
Cits risinājuma variants: \(P=\frac{Q}{t}\space\implies\space Q=Pt=150\cdot14=2100\space\mathrm{J}\)
\(Q=cm\Delta\mathrm{\Theta}\space\implies\space c=\frac{Q}{m\Delta\mathrm{\Theta}}=\frac{2100}{0,025\cdot20}=4200\space\mathrm{\frac{J}{kg\cdot K}}\). Tātad, ūdenim īpatnējā siltumietilpība ir divas reizes lielāka nekā ledum.
4. Posmā x ledus ir cietā, kristāliskā stāvoklī, posmā z ūdens ir šķidrā stāvoklī. Par vielas daļiņu kustības raksturu vari uzzināt "Fiztēmās".
Atbilde: Posmā x ūdens molekulas ledus kristālrežģī svārstās ap līdzsvara stāvokļiem. Posmā z ūdens molekulas šķidrumā kustas haotiski, brīvi.
5. Posms x atbilsts ledus silšanai, posms y – ledus kušanai, posms z – šķidra ūdens silšanai.
Pēc tam kad sasniegta kušanas temperatūra, kušanas laikā, turpinot pievadīt enerģiju, temperatūra paliek nemainīga. Labi zinām, ka normālā atmosfēras spiedienā ledus kūst un sacietē \(0\space\mathrm{^oC}\) temperatūrā.
Posmā x ledum silstot, palielinās vielas daļiņu vidējais kustības ātrums un, līdz ar to, arī svārstību frekvence un amplitūda ap daļiņu līdzsvara stāvokļiem. Rezultātā palielinās molekulu vidējā kinētiskā enerģija (K). Vielas daļiņām attālinoties, nedaudz mainās arī molekulu savstarpējās mijiedarbības enerģija P.
Kad ledus sasilis līdz kušanas temperatūrai, sāk izjukt molekulu regulārais izvietojums kristālā – tālā kārtība. Daļiņu mijiedarbība kļūst vājāka, būtiski pieaug daļiņu mijiedarbības potenciālā enerģija P. Tā kā daļiņu mijiedarbības potenciālo enerģiju vielā uzskata par negatīvu, tās skaitliskā vērtība kļūst mazāka.
Molekulas sāk kustēties brīvāk, kļūst iespējama translēcijas kustība. Ķermenis zaudē formu - kūst, pārvēršoties šķidrumā.
Ja turpina pievadīt siltumu, temperatūra nepaaugstinās, kamēr viss ledus nav izkusis. Tas nozīmē, ka visa pievadītā enerģija tiek patērēta daļiņu saišu "saraušanai". Tādēļ kušanas laikā daļiņu siltumkustības vidējā kinētiskā enerģija K nepalielinās un, līdz ar to, nepieaug temperatūra. Tikai tad, kad viela pilnībā izkususi, temperatūra un molekulu siltumkustības vidējā kinētiskā enerģija K atkal sāk pieaugt. Ieskaties arī Fiztēmās.
Atbilde:

6. Jāzina, ka absolūtā temperatūra ir molekulu vidējās kinētiskās enerģijas raksturlielums, tātad siltumkustība apstājas un molekulu kinētiskā enerģija vienāda ar nulli ir absolūtās nulles temperatūrā.
Atbilde: absolūtās nulles temperatūrā un/vai \(-273\space\mathrm{^oC}\) (vai \(-273,15\space\mathrm{^oC}\) vai \(-459,67\space\mathrm{^oF}\) vai \(0\space\mathrm{K}\))
1. Vērtēšanas kritēriji
- Nolasa no grafika temperatūras un laiku – 1 punkts.
- Uzraksta risinājuma gaitu un aprēķina sildītāja izdalīto siltuma daudzumu – 1 punkts.
- Uzraksta risinājuma gaitu un aprēķina īpatnējo siltumietilpību, norādot mērvienību – 1 punkts.
Ja skolēns izvēlējies risinājuma veidu, kas nav aprakstīts kritērijos, vērtētājs patstāvīgi sadala risinājumu soļos, atbilstoši dotajam punktu skaitam.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
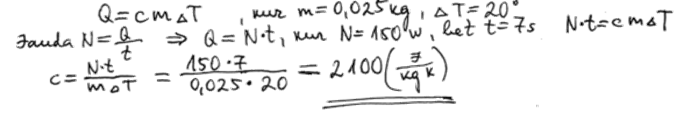
2. piemērs: risinājums novērtēts ar 2 punktiem. Kļūda izsakot īpatnējo siltumietilpību no formulas.
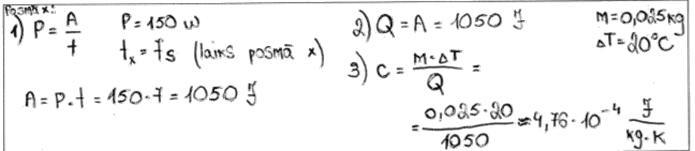
3. piemērs: risinājums novērtēts ar 1 punktu. Punkts piešķirts par īpatnējās siltumietilpības aprēķina formulu un pareizu mērvienību.
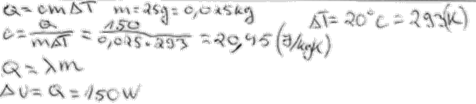
4. piemērs: risinājums novērtēts ar 0 punktu.
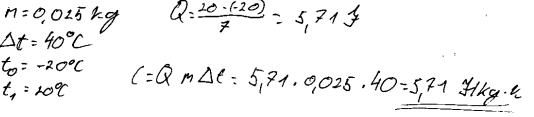
2. Vērtēšanas kritēriji
Nosauc kušanai atbilstošo grafika posmu UN nosaka kušanas ilgumu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
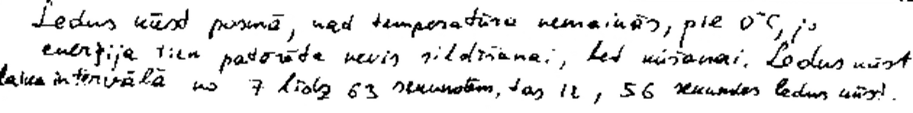
2. piemērs: risinājums novērtēts ar 1 punktu.

3. piemērs: risinājums novērtēts ar 0 punktu.
![]()
3. Vērtēšanas kritēriji
- Salīdzina silšanai atbilstošos grafika posmus un secina, ka ūdens silst lēnāk – 1 punkts.
- Secina, ka ūdens īpatnējā siltumietilpība ir lielāka – 1 punkts.
- Salīdzina ledus un ūdens īpatnējo siltumietilpību kvantitatīvi, secinot, ka ūdens īpatnējā siltumietilpība divreiz lielāka, nekā ledus (vai \(4200\space\mathrm{\frac{J}{kg\cdot K}}\)) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
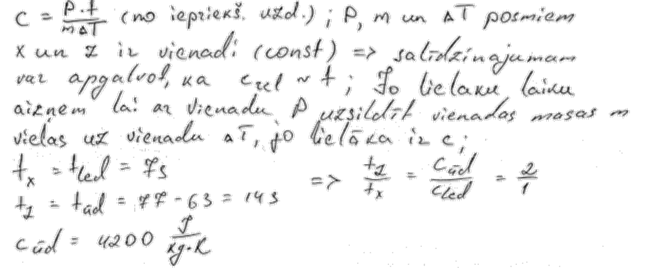
2. piemērs: risinājums novērtēts ar 3 punktiem.

3. piemērs: risinājums novērtēts ar 2 punktiem. Nav veikta kvantitatīva īpatnējās siltumietilpības salīdzināšana.
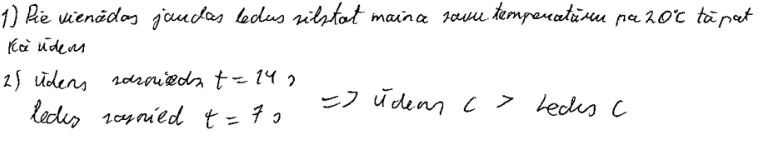
4. piemērs: risinājums novērtēts ar 1 punktu. Secina, ka ūdens īpatnēja siltumietilpība ir lielāka, bet nepareizi izvelas izejas datus no grafika.

5. piemērs: risinājums novērtēts ar 0 punktu.

4. Vērtēšanas kritēriji
Raksturo molekulu kustību abos grafika posmos – 1 punkts. Var būt salīdzināts arī molekulu kustības vidējais ātrums, tomēr, ja salīdzināts tikai tas, punktu neieskaita (posma x beigās un posma z sākumā tie vienādi un kustības rakstura salīdzinājums ir būtiski nepieciešams).
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
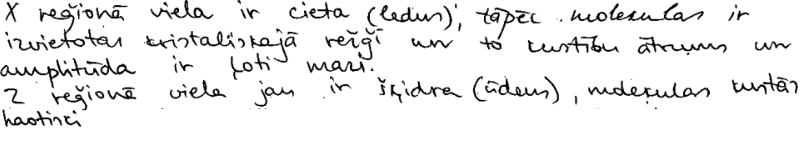
2. piemērs: risinājums novērtēts ar 2 punktu.
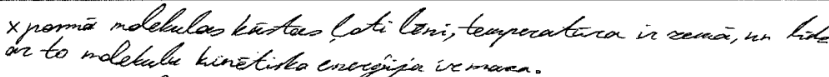
5. Vērtēšanas kritēriji
Zina, kura iekšējās enerģijas komponente ievērojami mainās katrā no posmiem (x – K; y – P; z – K) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.

2. piemērs: risinājums novērtēts ar 1 punktu.

3. piemērs: risinājums novērtēts ar 0 punktu.

6. Vērtēšanas kritēriji
Zina, ka molekulu kustība apstājas absolūtās nulles temperatūrā – 1 punkts.
Pamatojums nav nepieciešams. Pieļaujams nekorekts pamatojums, piemēram – uzrakstīta sakarība, kas saista molekulu vidējo kinētisko enerģiju un temperatūru ideālai gāzei.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
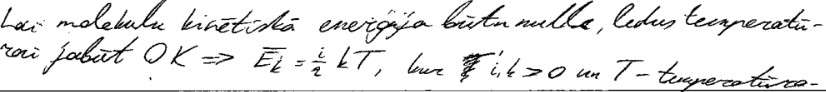
2. piemērs: risinājums novērtēts ar 1 punktu.
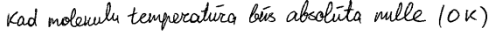
3. piemērs: risinājums novērtēts ar 0 punktu.