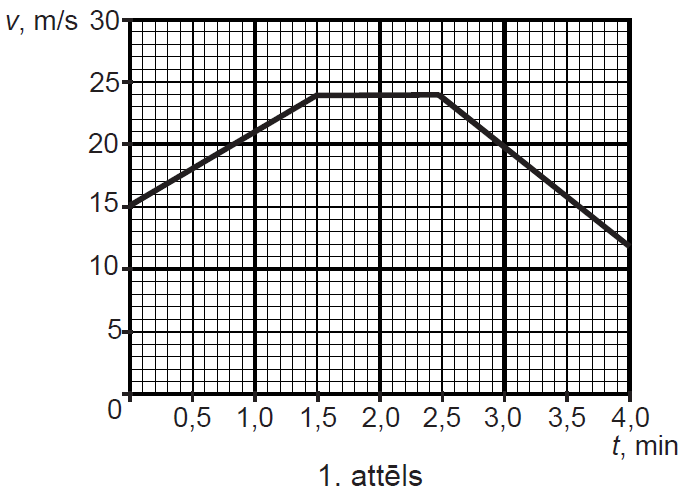
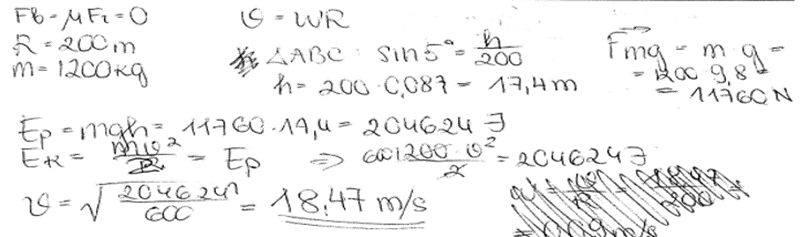Drīz Latvijā varētu sākt darboties vidējā ātruma radari. Sistēma darbojas šādi: transportlīdzeklim šķērsojot konkrētu ceļa posma robežu, pirmā mērierīce piefiksē šīs robežas šķērsošanas laiku, un, izbraucot no konkrētā ceļa posma, atkal tiek fiksēts laiks. Pēc tam aprēķina transportlīdzekļa vidējo ātrumu konkrētajā ceļa posmā un to salīdzina ar šajā vietā oficiāli atļauto braukšanas ātrumu. Automašīnas, kas pārvietojas starp abām kamerām, ātruma atkarība no laika parādīta 1. attēlā.
1. Vidējā ātruma ierobežojums šajā automaģistrāles posmā starp abām kamerām ir 80 km/h. Nosaki, vai automašīna pārsniedz atļauto braukšanas ātrumu! (2 punkti)
2. Ceļu satiksmes noteikumi nosaka, ka vadītājam ir jāizvēlas tāda distance \(d\), lai, priekšā braucošajam transportlīdzeklim bremzējot, būtu iespējams izvairīties no sadursmes. Distances \(d\) izvēles pamatā ir autovadītāju reakcijas laiks, nevis laiks, kas nepieciešams, lai mašīnu apturētu.
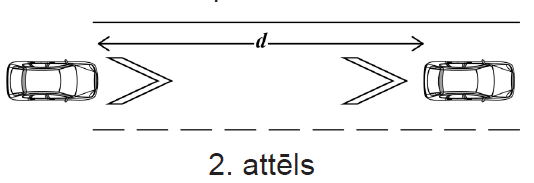
Pētījumi liecina, ka tipisks autovadītāju reakcijas laiks uz situācijas izmaiņām ir no 1,6 s līdz 2,0 s. Iesaki, kādam jābūt minimālajam attālumam \(d\), ja vidējā ātruma ierobežojums ir 110 km/h! (1 punkts)
3. Automašīna sāk bremzēt, kad tās ātrums ir 110 km/h, un apstājas. Automašīnas kopējā masa ir 1200 kg. Vidējais bremzēšanas spēks, kas iedarbojas uz automašīnu, ir 6,8 kN. Aprēķini laiku, kas nepieciešams, lai apturētu automašīnu, un automašīnas nobraukto attālumu bremzēšanas laikā! (3 punkti)
4. Automaģistrāles līkumos ceļš ir slīps, lai, braucot lielā ātrumā, automašīnai būtu mazāka iespēja izslīdēt no joslas. 3. attēlā parādīta automašīna, kas pārvietojas ceļa līkumā, kura rādiuss ir 200 m. Automaģistrāles slīpuma leņķis ir 5,0°. Smaguma spēks \(\overrightarrow{F}_\mathrm{SM}\) un reakcijas spēks \(\overrightarrow{F}_\mathrm{R}\), kas darbojas uz automašīnu, parādīti 4. attēlā.
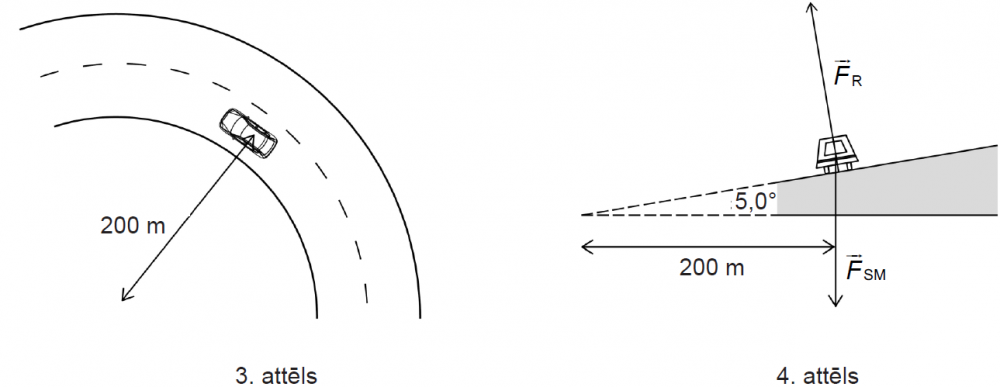
Ieteicamais ātrums līkumā ir tāds, lai berzes spēks, kas darbojas lejup pa nogāzi perpendikulāri kustības virzienam, būtu vienāds ar nulli. Aprēķini ieteicamo ātrumu šajā situācijā! (4 punkti)
1. punkts
Vidējā ātruma radari nosaka transporta līdzekļu kustības VIDĒJO ātrumu kādā konkrētā ceļa posmā. Tātad, šoreiz jāatbild uz jautājumu – vai pārsniegts atļautais VIDĒJAIS kustības ātrums. Tam, ka kādā brīdī ātrums ir bijis lielāks par maksimālo atļauto vidējo ātrumu, nav nozīmes.
Vidējo ātrumu aprēķina, dalot visu kustības laikā veikto ceļu ar kopējo kustības laiku: \(v_\mathrm{vid}=\frac{l_\mathrm{kop}}{t}\).
Šajā gadījumā veiktais ceļš skaitliski vienāds ar laukumu zem ātruma grafika atkarībā no laika.
Aprēķinot pa posmiem veikto ceļu, iegūsim: \({l_\mathrm{kop}}=1755\space\mathrm{m}+1440\space\mathrm{m}+1620\space\mathrm{m}=4815\space\mathrm{m}\)
Kustības vidējais ātrums \(v_\mathrm{vid}=\frac{l_\mathrm{kop}}{t}=\frac{4815\space\mathrm{m}}{240\space\mathrm{s}}\approx20{,}1\space\mathrm{m/s}\)
Lai salīdzinātu aprēķināto automašīnas kustības vidējo ātrumu ar atļauto braukšanas ātrumu, japārveido atļautā vidējā ātruma mērvienība: \(80\space\mathrm{km/h}=\frac{80000\space\mathrm{m}}{3600\space\mathrm{s}}=22{,}2\space\mathrm{m/s}\).
\(20{,}1\space\mathrm{m/s}<22{,}2\space\mathrm{m/s}\), tātad, automašīna nepārsniedz atļauto braukšanas ātrumu.
Var spriest arī savādāk. Aprēķinot nobraukto attālumu, braucot vienmērīgi ar vidējā ātruma ierobežojumam atbilstošo ātrumu \(22{,}2\space\mathrm{m/s}\), iegūst \(l=v_\mathrm{vid}t=22{,}2\space\mathrm{m/s}\cdot 240\space\mathrm{s}=5328\space\mathrm{m}\). Šī vērtība ir lielāka par nobraukto attālumu. Tātad, automašīnas vidējais ātrums bija mazāks par atļauto braukšanas ātrumu. Automašīna nepārsniedz atļauto braukšanas ātrumu.
Atbilde: nē, automašīna nepārsniedz atļauto braukšanas ātrumu.
2. punkts
Uzdevumā teikts, ka distances \(d\) izvēles pamatā ir autovadītāja reakcijas laiks, nevis laiks, kas nepieciešams, lai mašīnu apturētu.
Norādīts tipiskā autovadītāja reakcijas laika intervāls. Tā kā nav iespējams paredzēt, kāds konkrētajā situācijā būs šis reakcijas laiks, novērtējot distanci jāizvēlas MAKSIMĀLĀ reakcijas laika vērtība – \(2{,}0\space\mathrm{s}\).
Pārveidojot atļautā vidējā ātruma mērvienību, iegūst: \(110\space\mathrm{km/h}=\frac{110000\space\mathrm{m}}{3600\space\mathrm{s}}\approx30{,}6\space\mathrm{m/s}\).
Izmantojot reakcijas laiku \(2,0\space\mathrm{s}\), aprēķina minimālo attālumu \(d=v\cdot t=30{,}6\space\mathrm{m/s}\cdot 2{,}0\space\mathrm{s}=61{,}2\space\mathrm{m}\) (tika pieņemta arī atbilde \(60\space\mathrm{m}\)).
Pieļaujams arī risinājuma variants, šim attālumam pieskaitot klāt 1.3. jautājumā aprēķināto bremzēšanas ceļu (uzdevuma formulējumu var saprast arī šādi).
Atbilde: minimālajam attālumam \(d\) jābūt \(\approx61\space\mathrm{m}\).
3. punkts
Zinot kustības sākuma ātrumu, bremzēšanas laiku var aprēķināt, ja uzzina kustības paātrinājumu \(a\). To, savukārt, var uzzināt, izmantojot otro Ņūtona likumu: \(a=\frac{F}{m}=\frac{6800\space\mathrm{N}}{1200\space\mathrm{kg}}\approx5{,}67\space\mathrm{m/s^2}\) (paātrinājuma absolūtā vērtība).
Pārveidojot atļautā vidējā ātruma mērvienību, iegūst: \(110\space\mathrm{km/h}=\frac{110000\space\mathrm{m}}{3600\space\mathrm{s}}\approx30{,}6\space\mathrm{m/s}\).
Bremzēšanas laiks: \(t=\frac{v_0-0}{a}=\mathrm{\frac{30{,}6\space m/s}{5{,}67\space m/s^2}}\approx5{,}4\space\mathrm{s}\).
Bremzēšanas laiku var noteikt, nerēķinot kustības paātrinājumu, bet izmantojot datu bukletā atrodamo sakarību, kas saista spēku ar ķermeņa impulsa izmaiņu: \(F=\frac{\Delta p}{\Delta t}\), no kurienes \(\Delta t=\frac{\Delta p}{F}=\frac{mv_0-mv}{F}=\mathrm{\frac{1200\space kg\cdot30,6\space m/s-0}{6800\space N}}\approx5,4\space\mathrm{s}\).
Zinot kustības bremzēšanas laika un/vai kustības paātrinājuma vērtību, aprēķina bremzēšanas ceļu. To var izdarīt vairākos veidos:
1) izmantojot sakarību \(s=v_0t-\frac{at^2}{2}=\mathrm{30{,}6\cdot5{,}4-\frac{5{,}67\cdot5,4^4}{2}}\approx82{,}6\space \mathrm{m}\)
2) izmantojot kustības vidējo ātrumu \(s=v_\mathrm{vid}t=\frac{v_0}{2}t=\frac{30,6}{2}\cdot5,4\approx82,6\space\mathrm{m}\)
3) izmantojot datu bukletā atrodamo sakarību \(v^2-v_0^2=2as\). Izsakot bremzēšanas ceļu, iegūst: \(s=\frac{v^2-v_0^2}{2a}=\frac{0^2-30{,}6^2}{2\cdot(-5{,}67)}\approx82{,}6\space\mathrm{m}\)
4) izmantojot enerģijas nezūdamības likumu – automašīna kinētiskā enerģija, pretestības spēkiem veicot darbu, pārvēršas siltumenerģijā: \(W_\mathrm{k}=\frac{mv_0^2}{2}=A=F\cdot s\space\implies\space s=\frac{mv_0^2}{2F}=\frac{1200\cdot30{,}6^2}{2\cdot6800}\approx82{,}6\space\mathrm{m}\)
Atbilde: lai apturētu automašīnu, nepieciešamais laiks ir aptuveni \(5{,}4\space\mathrm{s}\). Bremzēšanas laikā nobrauktais attālums ir \(82{,}6\space\mathrm{m}\)
4. punkts
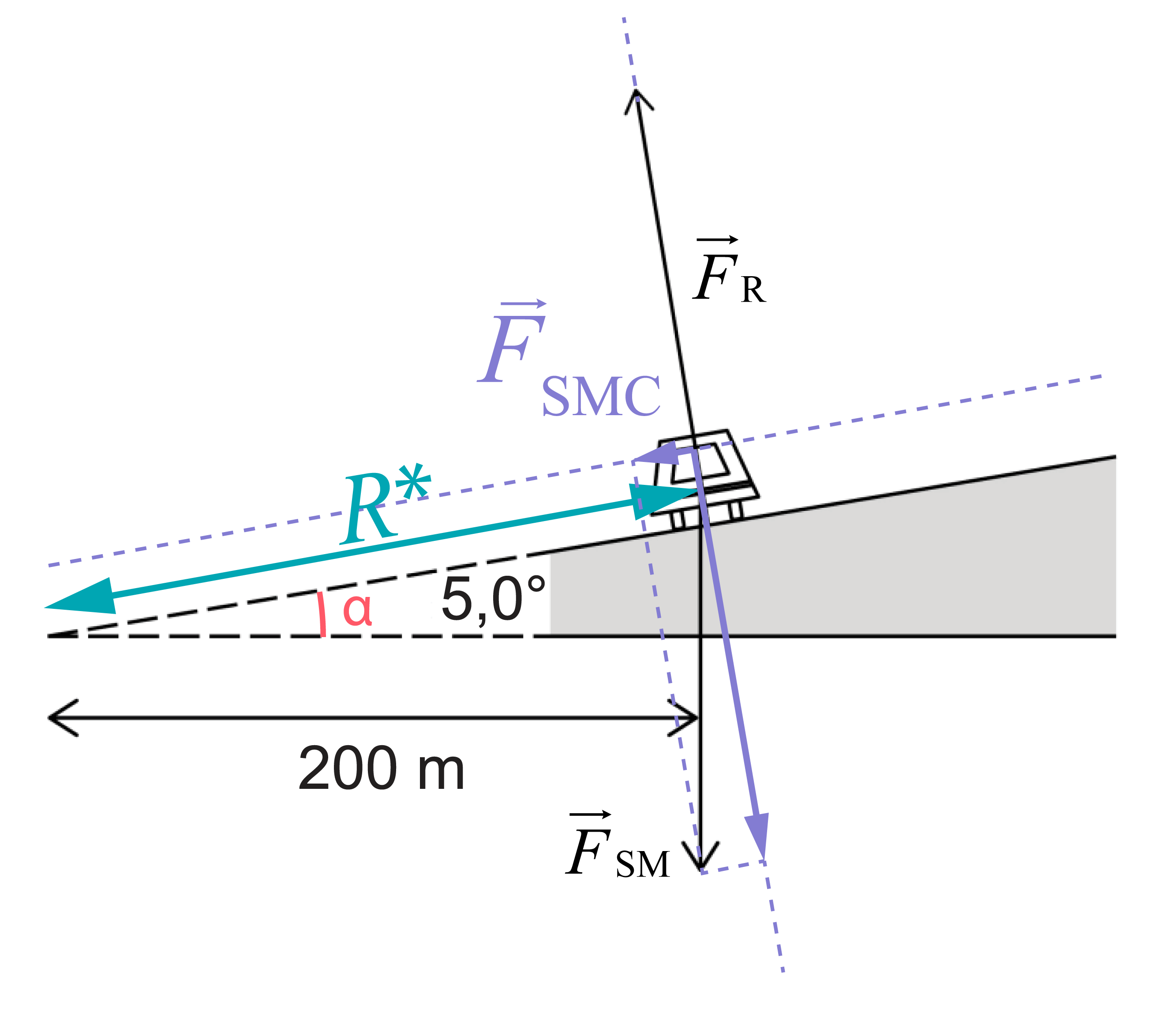Berzes spēks ir vienāds ar nulli, ja centrtieces paātrinājumu, ķermenim kustoties pa liektu trajektoriju, pilnībā nodrošina smaguma spēka un komponente \(\overrightarrow{F}_\mathrm{SMC}\), kas paralēla slīpajai ceļa plaknei un vērsta uz ceļa līkuma liekuma centru.
\({F}_\mathrm{SMC}=mg\sin{\alpha}\)
Jāņem vērā, ka uzdevumā dotais ceļa liekuma rādiuss mērīts pa horizontāli, nevis gar slīpo ceļa virsmu.
Savukārt, aprēķinot centrtieces paātrinājumu, ko iegūst automašīna aplūkotajā situācijā, jāņem vērā, ka kustības trajektorijas liekuma rādiuss \(R^*\) ir mazliet lielāks:
\(R^*=\frac{R}{\cos{\alpha}}\)
Izmantojot datu bukletā atrodamo formulu uzraksta otro Ņūtona likumu šajā gadījumā: \(mg\sin{\alpha}=ma_\mathrm{c}\)
\(mg\sin{\alpha}=m\frac{v^2}{R^*}\) \(\implies\space mg\sin{\alpha}=\frac{mv^2\cos{\alpha}}{R}\)
Izdalot vienādības abas puses ar masu, iegūst:
\(v^2=\frac{g\sin{\alpha}R}{\cos{\alpha}}\) un, tātad \(v=\sqrt{R\cdot g \cdot \mathrm{tg{\alpha}}}=\sqrt{200\cdot9{,}8\cdot0{,}087}\approx13\space\mathrm{m/s}\)
Atbilde: ieteicamais ātrums šajā situācijā \(13\space\mathrm{m/s}\).
1. punkts.
Uzdevuma izpilde eksāmenā – 47%.
Vērtēšanas kritēriji
Zina, ka vidējo ātrumu aprēķina, kustības laikā veikto ceļu dalot ar kustības ilgumu – 1 punkts.
Sniedz atbildi, novērtējot vidējo ātrumu – 1 punkts.
Zīmīgo ciparu skaitu atrisinājumā nevērtē.
Skolēnu risinājumu un to vērtējumu piemēri
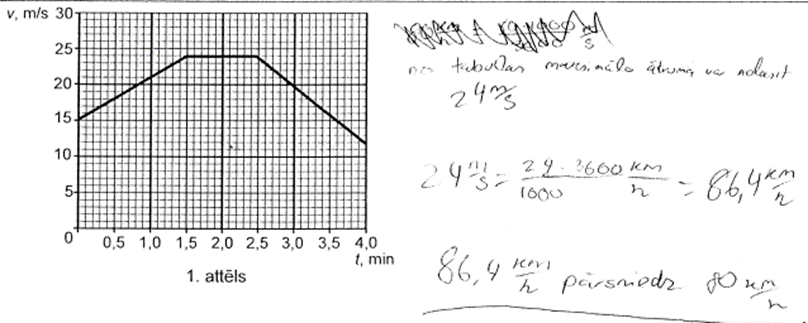
1. piemērs: risinājums novērtēts ar 2 punktiem.
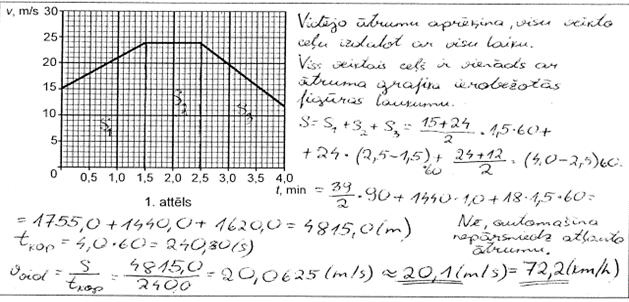
2. piemērs: risinājums novērtēts ar 2 punktiem.
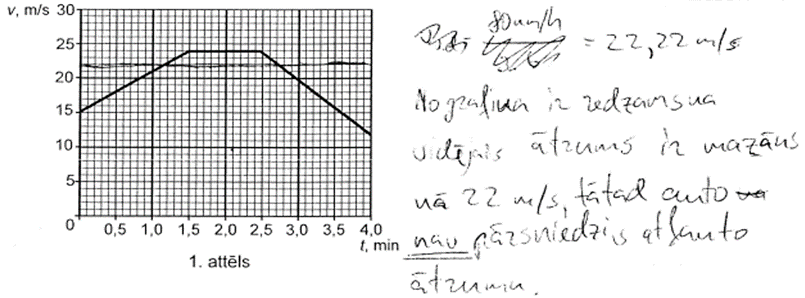
3. piemērs: risinājums novērtēts ar 1 punktu (nepareizi aprēķināts automašīnas veiktais ceļš pēc dotā ātruma grafika).
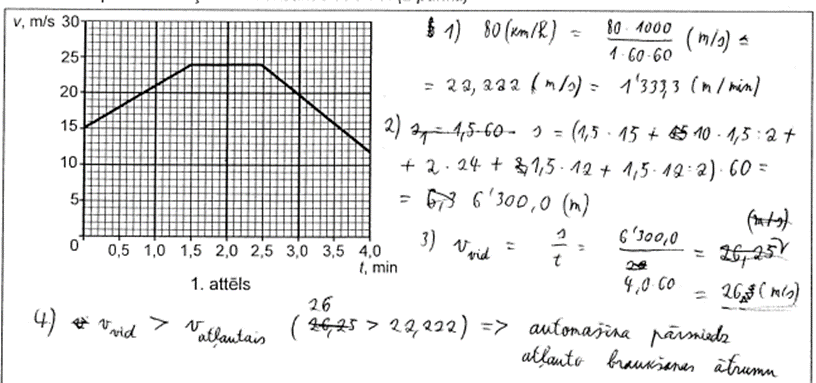
4. piemērs: risinājums novērtēts ar 0 punktu (ideja nav saprasta pareizi, vidējais ātrums nav aprēķināts).
2. punkts.
Uzdevuma izpilde eksāmenā – 44,6%.
Vērtēšanas kritēriji
Izmantojot tekstā doto faktu, ka distances (minimālā attāluma) \(d\) izvēles pamatā ir reakcijas laiks, un maksimālo reakcijas laiku – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
2. piemērs: risinājums novērtēts ar 1 punktu.
3. piemērs: risinājums novērtēts ar 1 punktu. Izmantots minimālais reakcijas laiks, bet saskatāma izpratne par to, ka šis ir tikai situācijā, ja autovadītāja reakcija ir laba.
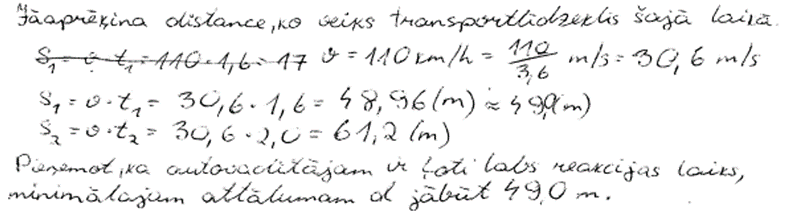
4. piemērs: risinājums novērtēts ar 0 punktu. Izmantots minimālais reakcijas laiks.
3. punkts.
Uzdevuma izpilde eksāmenā – 51,5%.
Vērtēšanas kritēriji
Ir risinājuma gaita bremzēšanas laika \(t\) aprēķināšanai (formula un/vai formulā ievietoti skaitļi) – 1 punkts.
Ir risinājuma gaita nobrauktā attāluma \(s\) aprēķināšanai (formula un/vai formulā ievietoti skaitļi) – 1 punkts.
Veikti skaitliskie aprēķini, visi rezultāti pierakstīti ar atbilstošajām mērvienībām (pieļaujama viena kļūda) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
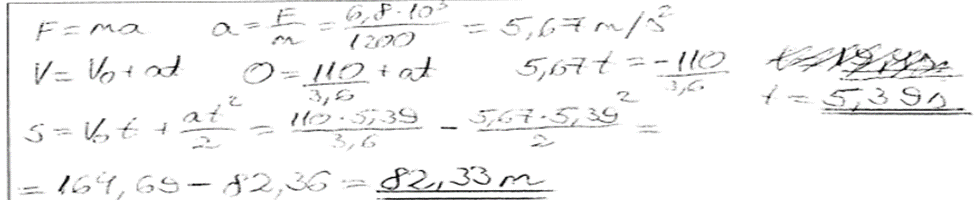
2. piemērs: risinājums novērtēts ar 3 punktiem.
3. piemērs: risinājums novērtēts ar 2 punktiem. Aprēķināts tikai bremzēšanas laiks, aprēķini pareizi.
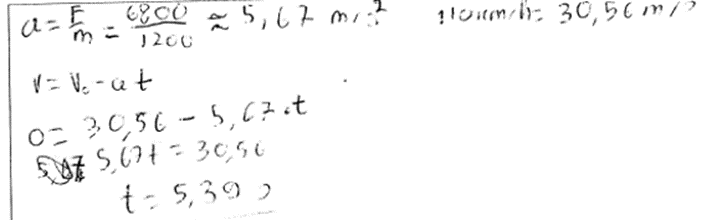
4. piemērs: risinājums novērtēts ar 2 punktiem. Viens būtiski kļūdains solis.
5. piemērs: risinājums novērtēts ar 1 punktu. Rēķināts tikai laiks, aprēķināts nepareizi, nepārveidojot ātruma mērvienību.
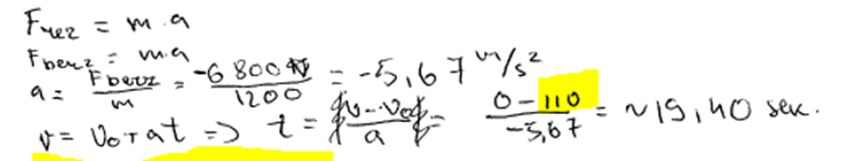
4. punkts.
Uzdevuma izpilde eksāmenā – 17,1%.
Vērtēšanas kritēriji
Izvērtē, kādā gadījumā berzes spēks būs vienāds ar nulli – 1 punkts
Izmanto leņķi, lai izteiktu smaguma spēka komponenti un trajektorijas rādiusu (formulas un/vai formulās ievietoti skaitļi) – 1 punkts
Pielīdzina smaguma spēka komponenti centrtieces spēkam – 1 punkts
Viss korekti aprēķināts, norādot arī mērvienības – 1 punkts
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem.
2. piemērs: risinājums novērtēts ar 4 punktiem. Nav aprēķināts \(R^*\), bet to, vērtējot, neņem vērā.
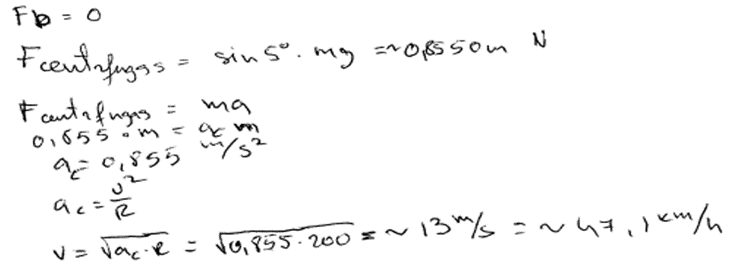
3. piemērs: risinājums novērtēts ar 3 punktiem. Formāli \(R\) izrēķināts, bet nav saprasts, ka berzes spēks vienāds ar nulli.
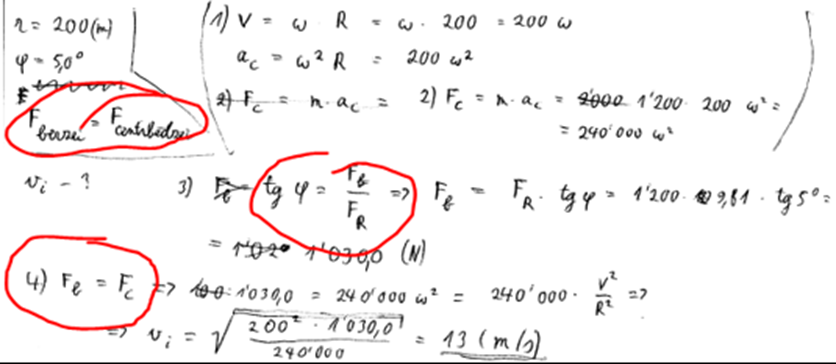
4. piemērs: risinājums novērtēts ar 2 punktiem. Trūkst izpratnes par to, kura smaguma spēka komponente kādā virzienā darbojas. Šādā situācijā atņemts punkts arī par to, ka nav rēķināts \(R^*\).
5. piemērs: risinājums novērtēts ar 1 punktu (punkts ir piesķirts par ideju, ka jāizmanto centrtieces paātrinājums, saistot to ar kustības ātrumu).
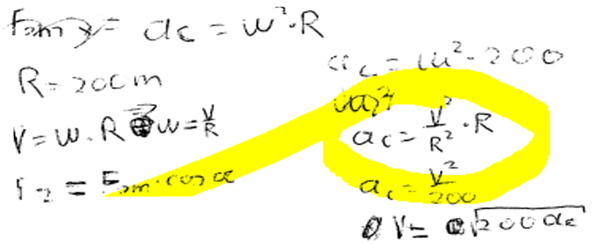
6. piemērs: risinājums novērtēts ar 0 punktu. Daudz sarakstīts, bet risinājuma nav.
