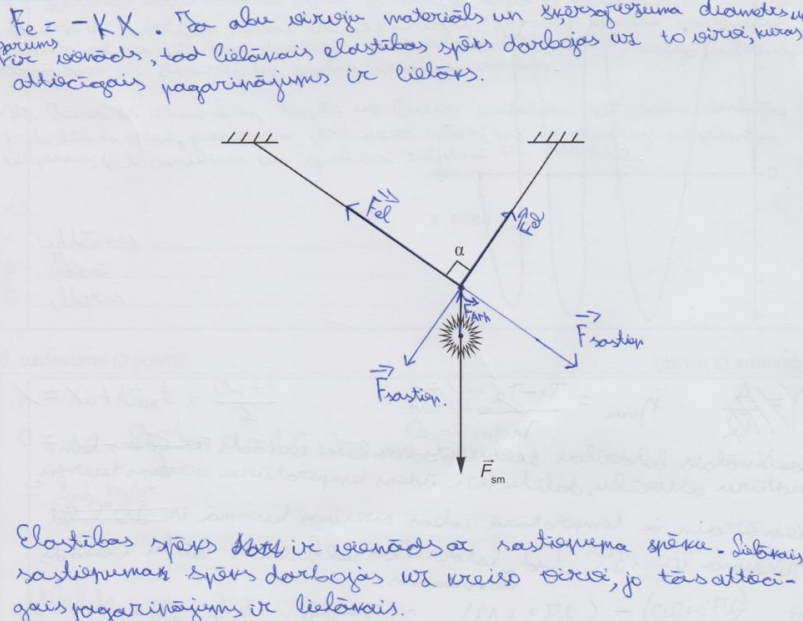
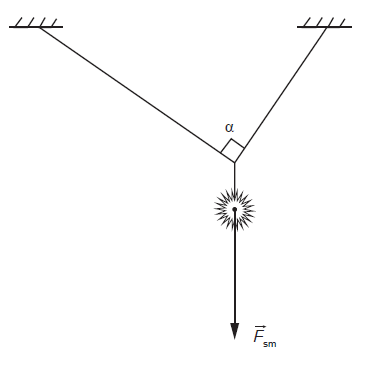
Hallē pie griestiem ir nepieciešams iekarināt apgaismes objektu tā, kā parādīts zīmējumā. Ir zināms, ka uz objektu darbojas smaguma spēks \(\overrightarrow{F}_\mathrm{sm}\). Leņķis \(\alpha\) starp abām auklām ir 90°. Zīmējums ir uzzīmēts mērogā.
Virvju masu neņem vērā!
Nosaki un pamato, uz kuru no virvēm darbojas lielāks sastiepuma spēks! Attēlo spēkus zīmējumā!
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Uzdevuma risināšanā ieteicams izmantot lineālu.
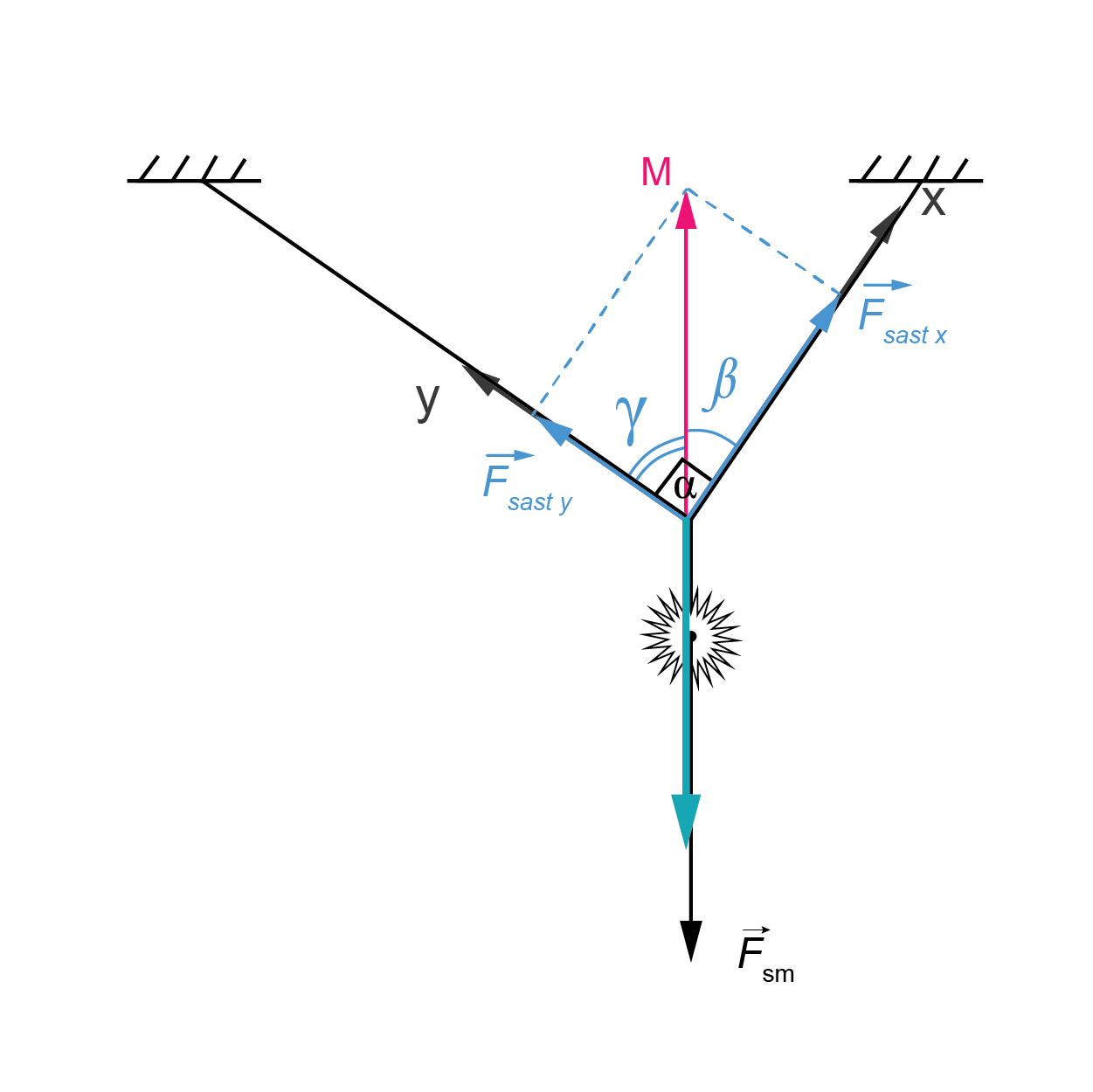
Aplūkosim A punktu (skatīt attēlu). Punkts A atrodas līdzsvara stāvoklī, tāpēc visi spēki, kas pielikti punktam A ir kompensēti jeb ir līdzsvarā. Punktam A ir pielikti divi auklu sastiepuma spēki \(\overrightarrow{F}_\mathrm{sast\space x}\), \(\overrightarrow{F}_\mathrm{sast\space y}\) un apgaismes objekta svars, kas skaitliski vienāds ar apgaismes objekta smaguma spēku \(\overrightarrow{F}_\mathrm{sm}.\)
1. risinājuma variants
Līdzsvara nosacījums: \(\overrightarrow{F}_\mathrm{sast\space x}+\overrightarrow{F}_\mathrm{sast\space y}+\overrightarrow{F}_\mathrm{sm}=\overrightarrow{0}\)
Tātad, \(\overrightarrow{F}_\mathrm{sast\space x}+\overrightarrow{F}_\mathrm{sast\space y}=-\overrightarrow{F}_\mathrm{sm}\)
Attēlā spēks \(\overrightarrow{F}_\mathrm{sm}\) ir attēlots no punkta A, tā vektora garums ir vienāds ar vektora \(\overrightarrow{\mathrm{AM}}\) garumu. Vektors \(\overrightarrow{\mathrm{AM}}\) ir vienāds ar abu sastiepuma spēku vektoru summu.
No punkta A konstruē divas koordinātu asis (X un Y), pēc uzdevuma teksta leņķis starp auklām (starp koordinātu asīm) ir 90°. Uzzīmē nogriežņa AM divas projekcijas uz X un Y asīm. No attēla ir redzams, ka \(F_\mathrm{sast\space x}>F_\mathrm{sast\space y}\)
Var paņemt transportieri un pārliecināties, ka leņķis \(\beta\) ir mazāks, nekā leņķis \(\gamma\).
\(F_\mathrm{sast\space x}=\mathrm{AM}\cos{\beta}\) un \(F_\mathrm{sast\space y}=\mathrm{AM}\cos{\gamma}\)
Ja \(\beta<\gamma\), tad \(\cos{\beta}>\cos{\gamma}\) un \(F_\mathrm{sast\space x}>F_\mathrm{sast\space y}\)
Atbilde: uz labās puses virvi darbojas lielāks sastiepuma spēks nekā uz kreisās puses virvi.
2. risinājuma variants
Uz gaismas objektu darbojas uz leju vērsts smaguma spēks \(\overrightarrow{F}_\mathrm{sm}\). Tā kā gaismas objekts atrodas līdzsvara stāvoklī, tad uz to darbojas vertikāli augšup vērsts tik pat liels elastības spēks (zīmējumā atbilst nogrieznim AM).
Tā kā zīmējumā auklas novietotas 90o liela leņķī, tad ir izdevīgi sadalīt elastības spēku divās komponentēs \(\overrightarrow{F}_\mathrm{sast\space x}\) un \(\overrightarrow{F}_\mathrm{sast\space y}\), kas darbojas pa X asi un Y asi. Tā kā zīmējums attēlots mērogā, tad izmēra spēku \(\overrightarrow{F}_\mathrm{sast\space x}\) un \(\overrightarrow{F}_\mathrm{sast\space y}\) garumus ar lineālu. Iegūst, ka \(F_\mathrm{sast\space x}>F_\mathrm{sast\space y}\)
Atbilde: uz labās puses virvi darbojas lielāks sastiepuma spēks nekā uz kreisās puses virvi.
Uzdevuma izpilde eksāmenā - 21%.
Vērtēšanas kritēriji
Attēlo vertikāli uz augšu vērstu rezultējošo sastiepuma spēku kā vienlielu ar smaguma spēku - 1 punkts
Uzzīmē rezultējošā sastiepuma spēka projekcijas uz auklām (sadala rezultējošo sastiepuma spēku divās komponentēs) - 1 punkts (cits variants - papildinot zīmējumu un izmantojot trigonometriskāš sakarības taisnleņķa trijstūrī, nosaka leņķus, ko veido rezultējošais sastiepuma spēks un atbilstošie auklu sastiepuma spēki)
Izdara secinājumu par atbilstošo sastiepuma spēku lielumiem - 1 punkts
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.

2. piemērs: risinājums novērtēts ar 3 punktiem (līdzsvara nosacījums tiek aplūkots horizontālajā virzienā)
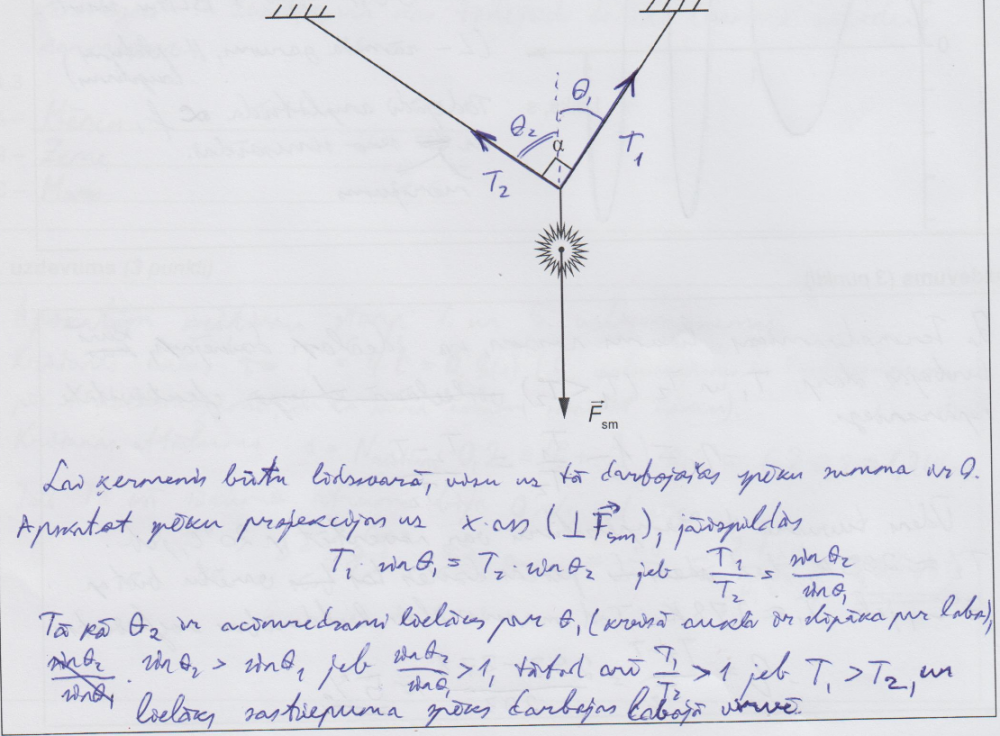
3. piemērs: risinājums novērtēts ar 3 punktiem.

4. piemērs: risinājums novērtēts ar 3 punktiem
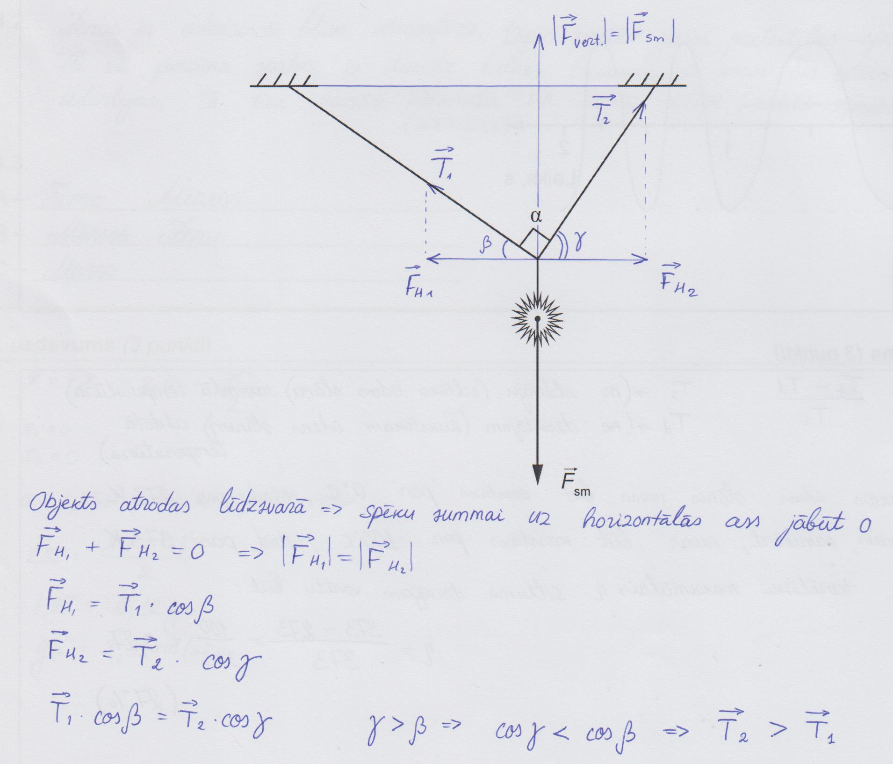
5. piemērs: risinājums novērtēts ar 2 punktiem (secinājuma pamatojums nav korekts).
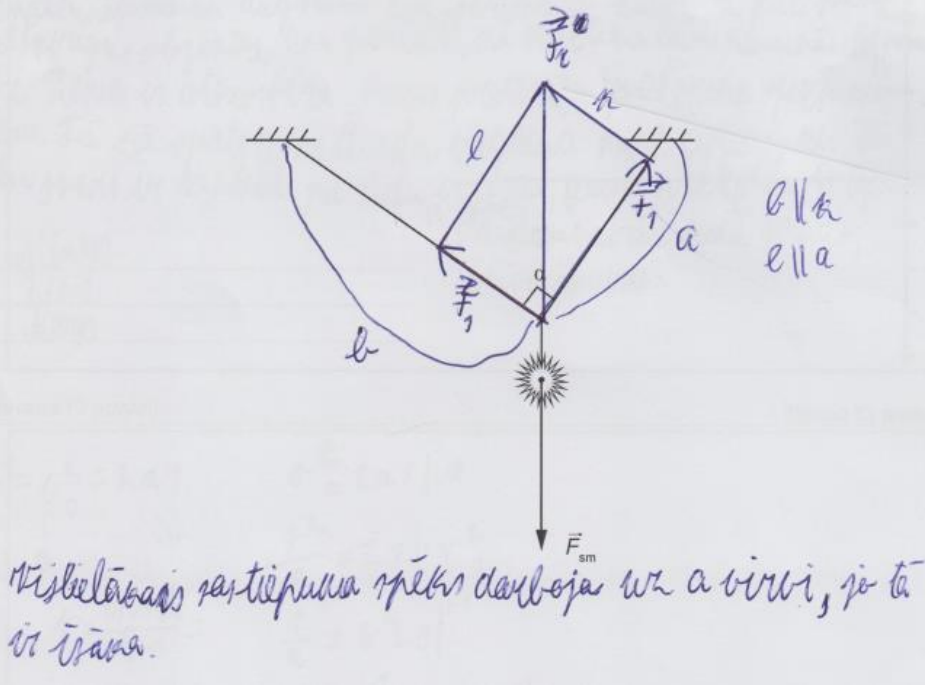
6. piemērs: risinājums novērtēts ar 1 punktu (virves garumam nav sakara ar leņķiem un sastiepuma spēku).
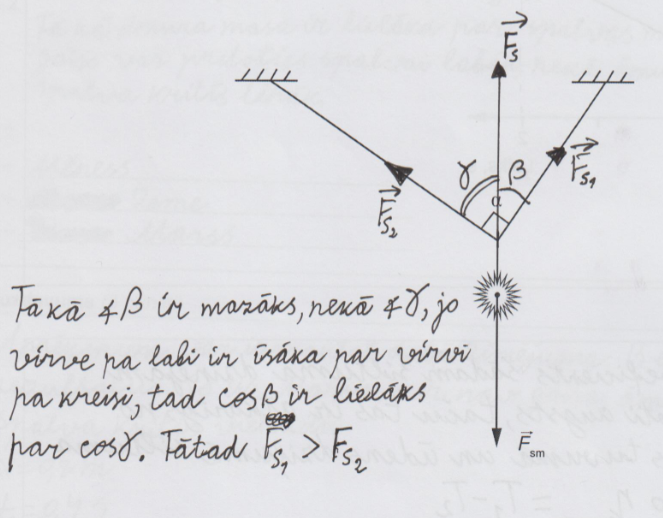
7. piemērs: risinājums novērtēts ar 0 punktiem (uzdevumā nekas nav teikts par auklu pagārinājumiem).