Lai ķermenis kļūtu par Zemes mākslīgo pavadoni un pārvietotos pa riņķveida orbītu, tam jāpiešķir pirmais kosmiskais ātrums. Gravitācijas spēks piešķir pavadonim centrtieces paātrinājumu. Izmantojot atbilstošas formulas no formulu lapas, iegūsti sakarību pirmā kosmiskā ātruma aprēķināšanai! Paskaidro, kas ir katrs lielums sakarībā!
1. variants
Shematiskajā attēlā Zemes mākslīgais pavadonis (ZMP) atrodas augstumā \(h\) virs Zemes virsmas. Tādēļ ZMP rotācijas rādiuss \(r\) ap Zemes centru ir vienāds \(r=R+h\), kur \(R\) – Zemes rādiuss. Gravitācijas spēks \(\overrightarrow{F_\mathrm{gr}}\), kas vērsts uz Zemes centru, piešķir pavadonim centrtieces paātrinājumu \(\overrightarrow{a_\mathrm{ct}}\).
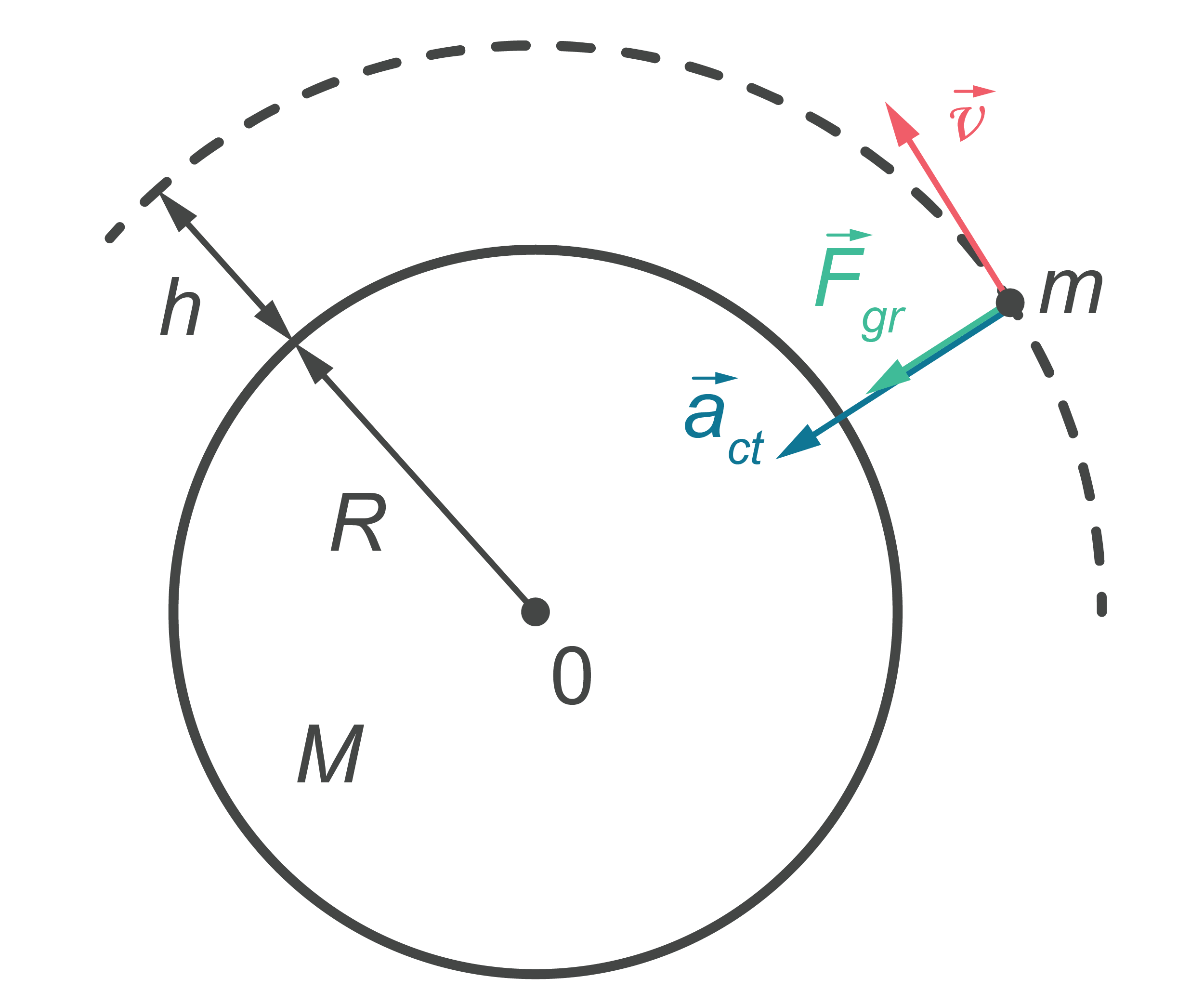
Lai noteiktu ZMP ātrumu \(v\) augstumā \(h\), izmanto gravitācijas likuma formulu \(F_\mathrm{gr}=G\frac{Mm}{r^2}\) (centrtieces spēks), otrā Ņūtona likuma formulu \(F_\mathrm{gr}=ma_\mathrm{ct}\) un centrtieces paātrinājuma formulu \(a_\mathrm{ct}=\frac{v^2}{r}\) kur \(M\) – Zemes masa, \(m\) – pavadoņa masa.
Iegūst:
\(G\frac{Mm}{r^2}=m\frac{v^2}{r}\)
\(G\frac{Mm}{(R+h)^2}=m\frac{v^2}{R+h}\)
Izsakot ZMP kustības ātrumu \(v\) uz orbītas: \(v=\sqrt{\frac{GM}{R+h}}\). Ja \(h\)= 0, tad \(v_1=\sqrt{\frac{GM}{R}}\).
Piezīme: ievērojot, ka \(g=\frac{GM}{R^2}\), iegūto izteiksmi var pārveidot \(v_1=\sqrt{\frac{GM}{R^2}\cdot R}=\sqrt{gR}\).
2. variants
Izteiksmi pirmā kosmiskā ātruma aprēķināšanai \(v_1=\sqrt{gR}\) var iegūst citādi. Jāatbild uz jautājumu: "Ar kādu ātrumu nepieciešams kustēties pa ideālo Zemes virsmu, lai centrtieces paātrinājums \(a_\mathrm{ct}\) būtu vienāds ar brīvo krišanas paātrinājumu \(g\)?"
Lai atbildētu uz šo jautājumu, brīvās krišanas paātrinājums japielīdzina centrtieces paātrinājumam: \(g=\frac{v^2}{R}\). Tādēļ \(v=\sqrt{gR}\).
Uzdevuma izpilde eksāmenā – 43%.
Vērtēšanas kritēriji
1. variants
Zina vai atrod formulu lapā gravitācijas spēka aprēķina formulu – 1 punkts.
Zina vai atrod formulu lapā otrā Ņūtona likuma un centrtieces paātrinājuma aprēķina formulu vai atceras centrtieces spēka aprēķina formulu – 1 punkts.
Apvieno izteiksmes un iegūst formulu ātruma aprēķināšanai, norāda, kas ir katrs lielums – 1 punkts.
2. variants
Zina vai atrod centrtieces paātrinājuma aprēķina formulu – 1 punkts.
Zina, ka brīvas krišanas paātrinājums ir vienāds centrtieces paātrinājumam – 1 punkts.
Iegūst formulu ātruma aprēķināšanai, norāda, kas ir katrs lielums – 1 punkts.