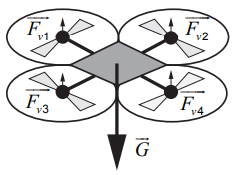
Drona jeb bezpilota lidaparāta pārvietošanās virzienu un lidošanas augstumu var kontrolēt, mainot propelleru griešanās ātrumu. Drons gaisā atrodas stabilā stāvoklī un nepārvietojas, kad visi drona propelleri griežas vienādā ātrumā un katri divi blakus esošie propelleri griežas pretējos virzienos. Cēlējspēks, kas rodas propellera darbības dēļ, līdzsvaro drona smaguma spēku.
Drona masa ir \(m=0,42\space\mathrm{kg}\), propellera vienas lāpstiņas garums \(d=0,21\space\mathrm{m}\), gaisa blīvums \(\rho=1,3\space\mathrm{kg/m^3}\), brīvās krišanas paātrinājums \(g=10\space\mathrm{m/s^2}\).
Aprēķini gaisa plūsmas ātrumu, ko rada drona propelleris! Pieņem, ka gaisa plūsmas ātrums ir vienāds visā laukumā, ko noklāj propellera lāpstiņas rotējot!
Parādi aprēķinu gaitu:
• izvēlies un uzraksti nepieciešamās likumsakarības (formulas);
• pieraksti formulās ietverto fizikālo lielumu nosaukumus, ja to apzīmējumi nesakrīt ar vispārpieņemtajiem;
• veic atbilstošus likumsakarību (formulu) pārveidojumus;
• strukturē risinājumu, ievēro loģisko secību;
• parādi visas matemātiskās darbības – katra fizikālā lieluma aprēķina formulā ievieto skaitļus, veic aprēķinus ar kalkulatoru vai galvā un pieraksti rezultātu ar mērvienību!
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Piedāvājam risinājumus, kuros izmantoti skolas kursā apgūstami uzdevuma situācijas modeļi.
Uz dronu gaisā darbojas smaguma spēks \(F_\mathrm {sm}=mg\), kas vērsts uz leju. Ja drons atrodas stabilā stāvoklī gaisā un nepārvietojas, tad jābūt spēkam, kas vērsts uz augšu un kompensē smaguma spēku.
1. metode. Impulsa nezūdamības likums vai III Ņūtona likums.
Propelleri grūž gaisu lejup ar spēku \(F\), gaiss ceļ dronu augšup ar tādu pašu spēku. Pielieto II Ņūtona likumu izteiktu ar impulsu: \(F=\frac{\Delta p}{\Delta t}\) , kur \(\Delta p\) – gaisa plūsmas impulsa izmaiņa laikā \(\Delta t\) (šo sakarību var iegūt, izmantojot formulu lapā atrodamās sakarības:
\(F=ma\); \(a=\frac{\Delta v}{\Delta t}\); \(p=mv\), tātad varam izteikt \(F=\frac{m\Delta v}{\Delta t}=\frac{\Delta p}{\Delta t}\)).
Gaisa impulsa izmaiņu \(\Delta p\) nosaka pēc formulas \(\Delta p=p_\mathrm b- p_\mathrm s\), kur \(p_\mathrm b\) – gaismas plūsmas beigu impulss \(p_\mathrm b=mv\), \(p_\mathrm s\) – gaisa plūsmas sākuma impulss, \(v\) – gaisa plūsmas beigu ātrums. Gaisa plūsmas sākuma impulss \(p_\mathrm s=0\), jo gaisa sākuma ātrums ir nulle. Tādēļ \(\Delta p=p_\mathrm b- p_\mathrm s=mv\).
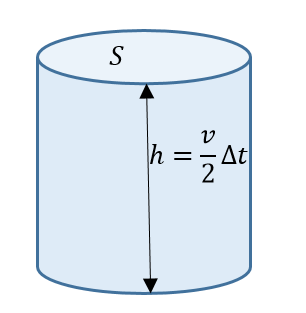
Tālāk jānosaka gaisa masa \(m\), ko laikā \(\Delta t\) propellers grūž uz leju. Zīmējumā (1. att.) ir parādīts gaisa tilpums \(V\), ko laikā \(\Delta t\) propellers rotējot grūž uz leju. Cilindra pamata laukums \(S\) ir laukums, ko aptver propellers rotējot. Pieņemot, ka gaisa kustība ir vienmērīgi paātrināta, gaisa plūsmas vidējais ātrums ir \(\frac{v}{2}\). Cilindra augstums ir vienāds \(\frac{v}{2}\Delta t\). Tad gaisa tilpumu \(V\), ko atgrūž propellers laikā \(\Delta t\) uz leju, nosaka šādi: \(\frac{v}{2}\Delta tS\). Gaisa masu \(m\) aprēķina pēc formulas \(m=\rho V=\rho \frac{v}{2}\Delta tS\), kur \(\rho\) – gaisa blīvums.
Tādēļ gaisa impulsa izmaiņa \(\Delta p=mv=\rho \frac{v}{2}\Delta t S\cdot v\)
Cēlējspēku tālāk nosaka pēc formulas \(F=\frac{\Delta p}{\Delta t}=\frac{\rho v^2S\Delta t}{2\Delta t}=\frac{\rho v^2S}{2}\)
Kopā dronam ir 4 propelleri. Tādēļ cēlējspēks \(F_\mathrm c=4F=4\frac{\rho v^2S}{2}=2\rho v^2S\)
Propellera aizņemto laukumu \(S\) nosaka pēc formulas \(S=\pi d^2\), kur \(d\) – propellera vienas lāpstiņas garums. Tad \(F_\mathrm c=2\rho v^2S=2\rho v^2\pi d^2\)
Pielīdzina drona cēlējspēku un smaguma spēku, iegūst izteiksmi \(mg=2\rho v^2 \pi d^2\). Izsaka propellera rotācijas ātrumu \(v=\frac{1}{d}\sqrt{\frac{mg}{2\rho \pi}}\).
2. metode. II Ņūtona likums: \(F=ma\).
Gaisa plūsma kustas uz leju un grūž dronu ar augšu. Spēks, ko veido gaisa plūsma, kompensē drona smaguma spēku.
\(F_\mathrm {sm}=F=ma=\rho Va=\rho S\frac{v}{2}\Delta ta\), kur \(S\frac{v}{2}\Delta t=V\) – gaisa plūsmas tilpums, ko propellers izgrūž uz leju ar paātrinājumu \(a\), piešķirot tām ātrumu \(v=a\Delta t\) . Tādēļ \(F=\rho S\frac{v}{2}\Delta ta=\frac{\rho v^2S}{2}\).
Propellera aptverto laukumu \(S\) nosaka pēc formulas \(S=\pi d^2\), kur \(d\) – propellera vienas lāpstiņas garums. Tad \(F_\mathrm c=4F=4\frac{\rho v^2S}{2}=2\rho v^2S\).
Pielīdzinot drona cēlējspēku un smaguma spēku, iegūst izteiksmi \(mg=2\rho v^2 \pi d^2\). Izsaka gaisa plūsmas ātrumu \(v=\frac{1}{d}\sqrt{\frac{mg}{2\rho \pi}}\).
Aprēķini
\(v=\frac{1}{d}\sqrt{\frac{mg}{2\rho \pi}}=\frac{1}{0,21}\sqrt{\frac{0,42\cdot 10}{2\cdot1,3\cdot3,14}}\approx 3,4\space\mathrm {m/s}\)
Piezīme
Atsevišķi var noteikt drona smaguma spēku \(F_\mathrm{sm}=mg\) un propellera aptverto laukumu, tam rotējot, \(S=\pi d^2\).
Aprēķini: \(F_\mathrm{sm}=mg=0,42\cdot10=4,2\space\mathrm N\)
\(S=\pi d^2=3,14\cdot0,21^2\approx0,138\space\mathrm{m^2}\)
Ja ar \(d\) apzīmē propellera garumu, nevis propellera lāpstiņas garumu, tad formulā \(d\) vietā jāraksta \(d/2\).
3. metode. Propellera jauda, veiktais darbs un gaisam piešķirtā enerģija.
Propellera jaudu \(N\) nosaka pēc formulas \(N=F_\mathrm c v\), kur \(F_\mathrm c\) – propellera radītais augšup vērstais spēks, \(v\) – gaisa plūsmas, kas iet caur propelleru, ātrums.
Gaisa masa \(m\), kas laikā \(\Delta t\) iziet caur propelleru, ir vienāda \(m=\rho V\), kur \(\rho\) – gaisa blīvums, \(V\) – gaisa tilpums, modelējot gaisa plūsmu kā cilindru. Cilindra tilpums \(V=sv\Delta t\), kur \(v\Delta t\) – gaisa veiktais ceļš laikā \(\Delta t\). Tādēļ gaisa masa \(m=\rho Sv\Delta t\).
Propellera veiktais darbs \(A\) ir vienāds \(A=N\Delta t=F_\mathrm cv\Delta t\).
Veiktais darbs ir vienāds gaisa plūsmas kinētiskās enerģijas izmaiņu: \(A=\Delta W_\mathrm{kin}\), kur \(\Delta W_\mathrm{kin}=\frac{mv^2}{2}-\frac{mv^2_0}{2}\). Pieņem, ka gaisa plūsmas sākuma ātrums ir vienāds ar 0. Tādēļ \(A=\frac{mv^2}{2}\).
Apvieno abas formulas: \(F_\mathrm c v\Delta t=\frac{mv^2}{2}\). Ievieto masas \(m\) vietā izteiksmi \(\rho Sv\Delta t\) un iegūst \(Fv\Delta t=\frac{\rho Sv\Delta t v^2}{2}\). Saīsina izteiksmes abas puses ar \(t\) un \(v\), un izsaka propellera radīto augšup vērsto spēku \(F_\mathrm c=\frac{\rho Sv^2}{2}\).
Propellera radītais spēks kompensē drona smaguma spēku: \(F_\mathrm c=mg\). Kopējais propelleru laukums, tam rotējot, ir \(4S=4\pi d^2\), kur \(d\) – propellera vienas lāpstiņas garums. Tādēļ \(mg=2\rho v^2 \pi d^2\) un gaisa plūsmas ātrums \(v=\frac{1}{d}\sqrt{\frac{mg}{2\rho \pi}}\).
Aprēķini
\(v=\frac{1}{d}\sqrt{\frac{mg}{2\rho \pi}}=\frac{1}{ 0,21}\sqrt{\frac{0,42\cdot 10}{2\cdot1,3\cdot3,14}}\approx 3,4\space\mathrm {m/s}\)
Uzdevuma izpilde eksāmenā - 11,5%.
Vērtēšanas kritēriji
Pielīdzina vertikāli augšup vērsto spēku smaguma spēkam vai izmanto mehāniskās enerģijas nezūdamības likumu – 1 punkts.
Uzraksta impulsa nezūdamības likumu propellera un gaisa mijiedarbībai vai spiediena spēka, vai pretspēka aprēķināšanas izteiksmes – 1 punkts.
Atrod gaisa masas aprēķināšanas izteiksmi, izmantojot dotos lielumus – 1 punkts.
Iegūst gaisa plūsmas ātruma aprēķināšanas izteiksmi – 1 punkts.
Aprēķina aptuveno gaisa plūsmas ātrumu un iegūst rezultātu robežās no 2 m/s līdz 10 m/s – 1 punkts.