2014. gadā inženieru grupa no Latvijas izstrādāja maza izmēra lidaparātu Airdog ekstrēmo sporta veidu filmēšanai, kas strauji guvis atzinību visā pasaulē. Šim lidaparātam ir četri rotori, un ar speciālas programmatūras palīdzību tas spēj darboties patstāvīgi, bez cilvēka vadības.
Iedomāsimies, ka Airdog seko velosportistam (V), kurš vienmērīgi pārvietojas pa riņķveida trajektoriju, kuras rādiuss \(100\space\mathrm m\). Lidaparāta (L) uzdevums ir filmēt sportistu, lidojot nelielā augstumā pa riņķveida trajektoriju, kuras rādiuss \(120\space\mathrm m\), tā lai punkts O, sportists un lidaparāts atrastos uz vienas taisnes.
1. Iezīmē attēlā sportista centrtieces paātrinājuma vektoru un lidaparāta ātruma vektoru!
2. Salīdzini sportista un lidaparāta apriņķojuma frekvences!
3. Pamato ar fizikas formulām, kā atšķiras sportista un lidaparāta lineārie ātrumi!
4. Novērtē, vai mainās lidaparāta smaguma spēks, ja tas paceļas par \(100\space\mathrm m\) augstāk? Atbildi pamato!
5. Ražotāji norāda, ka Airdog lidojuma ilgums bez uzlādes ir no \(10\) līdz \(20\) minūtēm. Mini divus apstākļus vai lidojuma īpatnības, kas var ietekmēt baterijas darbības laiku! Atbildi pamato!
1. Vienmērīgā kustībā pa riņķa līniju lineārā ātruma modulis ir nemainīgs, bet ātruma vektora virziens visu laiku mainās. Lidaparāta lineārā ātruma vektors \(\overrightarrow{v_\mathrm L}\) (attēlā uzzīmēts ar zilu krāsu) vērsts pa pieskari trajektorijai (skatīt 1. attēlu). Lidaparāta kustības virziens uzdevumā nav norādīts, tāpēc lineārā ātruma vektora virziens var būt arī pretējs attēlotajam.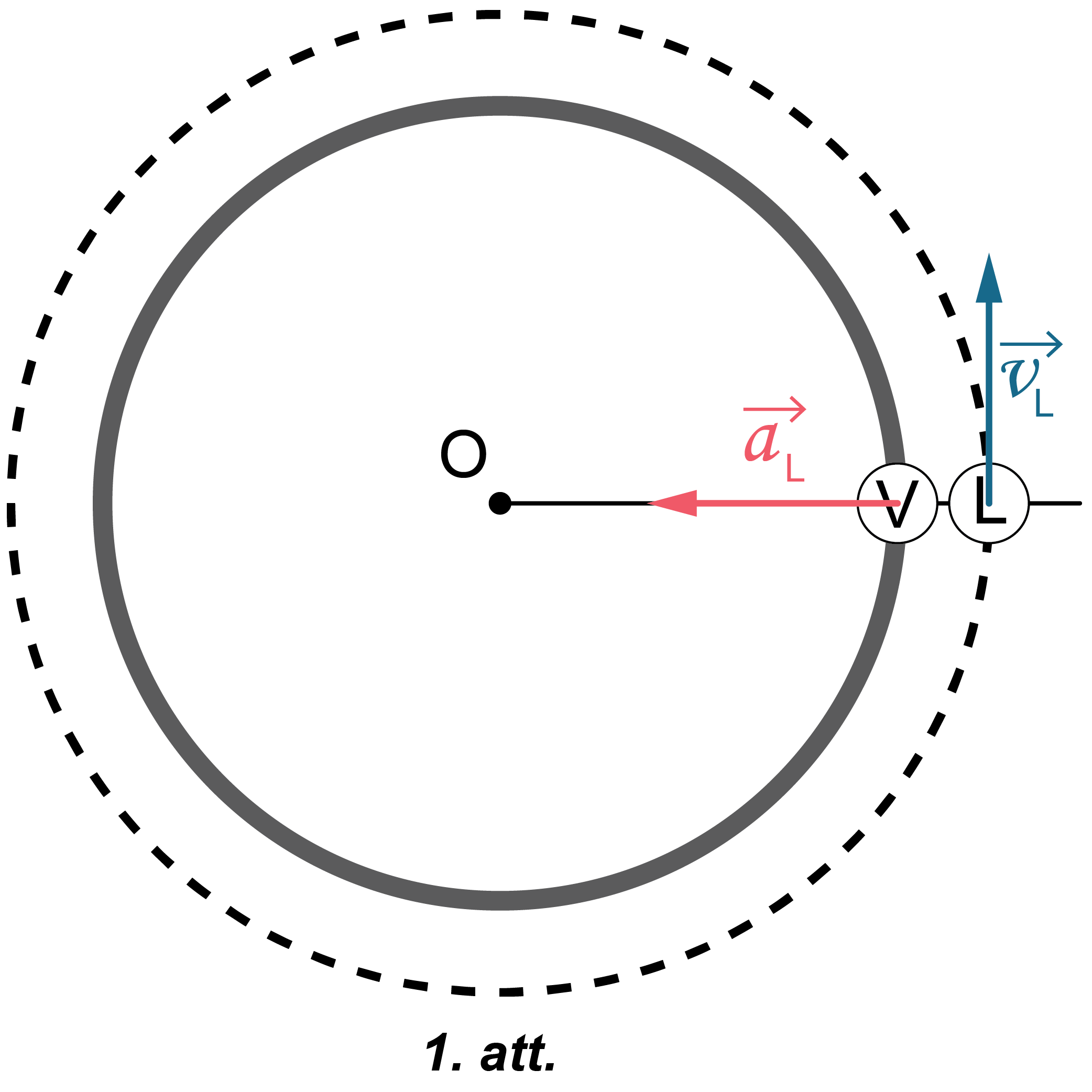
Tāpat kā lidaparāta, arī sportista lineārā ātruma vektors ir vērsts pa pieskari trajektorijai un visu laiku maina virzienu. Šo izmaiņu raksturo centrtieces paātrinājums \(\overrightarrow{a_\mathrm V}\). Zīmējumā sportista centrtieces paātrinājums attēlots ar sarkanās krāsas vektoru, un katrā trajektorijas punktā tas ir vērsts uz rotācijas centru O. (skatīt 1. attēlu)
2. Rotācijas periods \(T\) ir laiks, kurā ķermenis kustībā pa riņķa līniju veic vienu pilnu apgriezienu \(T=\frac{t}{N}\), kur \(t\) ir laiks, kurā ķermenis veic \(N\) apgriezienus. Tā kā sportists un lidaparāts visu laiku atrodas uz vienas taisnes, tad viņu rotācijas periodi ir vienādi.
Rotācijas frekvence \(f\) ir apgriezienu skaits vienā laika vienībā: \(f=\frac{N}{t}\). Frekvence ir rotācijas periodam apgriezts lielums \(f=\frac{1}{T}\). Tā kā sportista un lidaparāta rotācijas periodi ir vienādi, tad arī apriņķojuma frekvences ir vienādas.
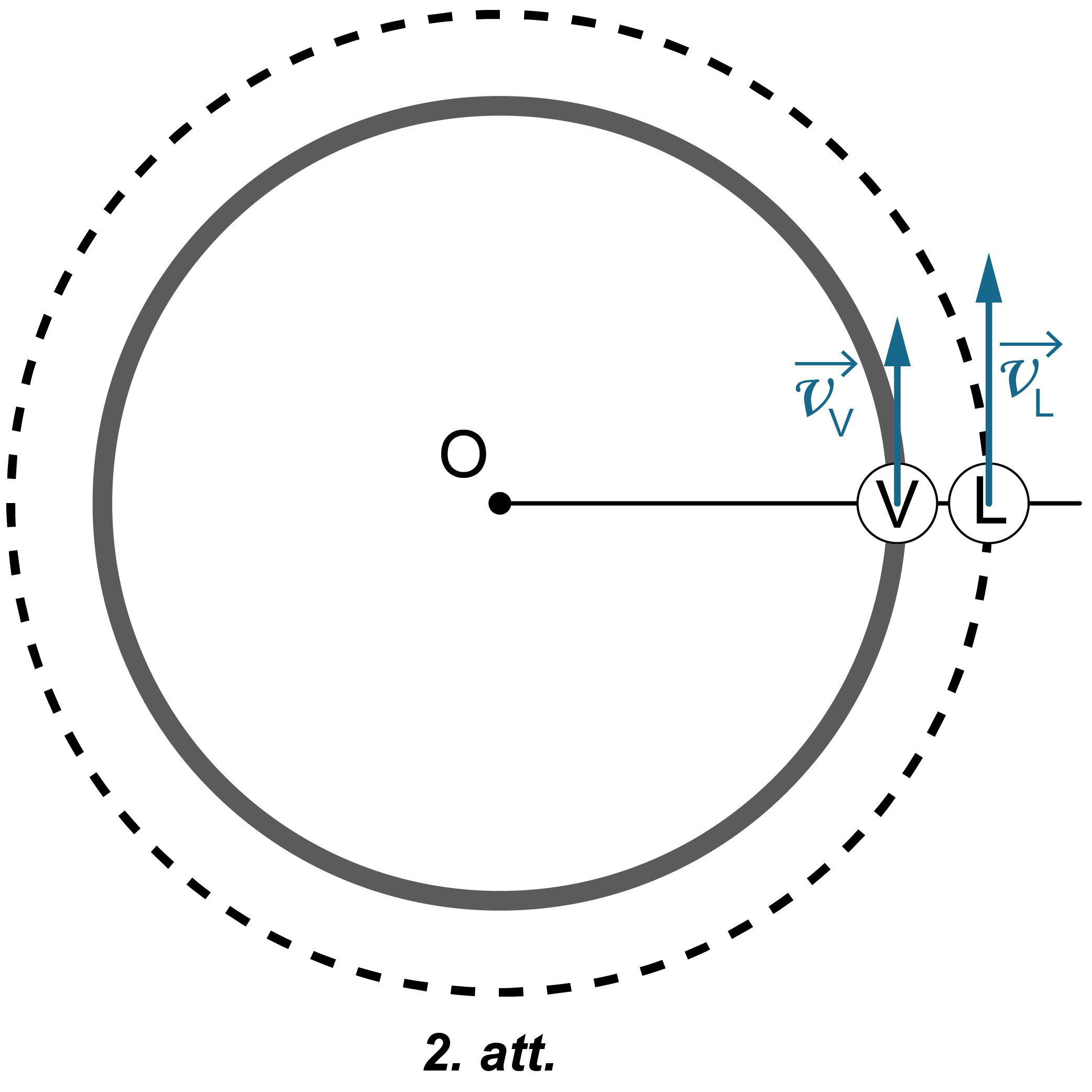
3. Ķermeņa lineāro ātrumu \(v\) aprēķina pēc formulas \(v=2\pi Rf\) vai \(v=\frac{2\pi R}{T}\), kur \(R\) – rotācijas rādiuss, \(T\) – rotācijas periods, \(f\) – rotācijas frekvence. No formulām redzams, ka lineārais ātrums \(v\) ir tieši proporcionāls rotācijas rādiusam \(R\), ja rotācijas periods (jeb frekvence) nemainās. Lidaparāta rotācijas rādiuss (\(120\space\mathrm m\)) ir lielāks nekā sportista rotācijas rādiuss (\(100\space\mathrm m\)). Tāpēc lidaparāta lineārā ātruma \(\overrightarrow{v_\mathrm L}\) modulim ir jābūt lielākam par sportista lineārā ātruma \(\overrightarrow{v_\mathrm V}\) moduli (skatīt 2. attēlu).
4.
1. variants
Lidaparāta smaguma spēku \(F_{\mathrm {sm}}\) aprēķina pēc formulas \(F_{\mathrm {sm}}=mg\), kur \(m\) – lidaparāta masa, \(g\) – brīvās krišanas paātrinājums. Zināms, ka brīvās krišanas paātrinājums ir atkarīgs no attāluma līdz Zemes centram – jo lielāks attālums, jo mazāks ir brīvās krišanas paātrinājums. Tāpēc, lidaparātam pārvietojoties \(100\space\mathrm m\) augstāk, smaguma spēks \(F_{\mathrm {sm}}\) nedaudz samazinās.
2. variants
Izmanto gravitācijas likumu \(F_{\mathrm {sm}}=G\frac{M_\mathrm Zm}{{(R_\mathrm Z+h)}^2}\), kur \(m\) – lidaparāta masa, \(G\) – gravitācijas konstante, \(M_\mathrm Z\) – Zemes masa, \(R_\mathrm Z\) – Zemes rādiuss, \(h\) – lidaparāta augstums virs Zemes. Lidaparātam, paceļoties par \(100\space\mathrm m\) augstāk, lielumi \(G, \space m,\space M_\mathrm Z\) un \(R_\mathrm Z\) nemainās, bet augstums \(h\) palielinās. Palielinoties augstumam, palielinās daļas saucēja \({(R_\mathrm Z+h)}^2\) vērtība, rezultātā samazinās visas izteiksmes vērtība. Tāpēc, lidaparātam pārvietojoties \(100\space\mathrm m\) augstāk, smaguma spēks \(F_{\mathrm {sm}}\) nedaudz samazinās.
5. Kas ietekmē baterijas darbības laiku?
a) Stiprs vējš. Lidaparātam vējā nepieciešams veikt sarežģītu balansēšanu, kam tiek patērēta papildu enerģija.
b) Kustība pret vēju. Jo stiprāks vējš, jo ātrāk griežas lidaparāta propelleri un iek patērēta lielaka enerģija.
c) Augsta temperatūra. Jo augstāka ir gaisa temperatūra, jo mazāks ir tā blīvums. Lidaparāta propelleriem jāgriežas ātrāk, lai noturētos gaisā tajā pašā augstumā, tāpēc pieaug enerģijas patēriņš.
d) Lidaparāta lidojums sporta režīmā patērē vairāk enerģijas, nekā parasts lidojums, jo sporta režīmā lidaparātam vairāk jāmanevrē.
e) Baterijas "vecums". Jo "vecāka" ir baterija, jo mazāks ir tās darbības laiks.
Vērtēšanas kritēriji
1. Iezīmē lidaparāta lineārā ātruma vektoru – 1 punkts. Iezīmē centrtieces paātrinājuma vektoru – 1 punkts.
2. Salīdzina sportista un lidaparāta apriņķojuma frekvences – 1 punkts.
3. Pamato ar fizikas formulām, kā atšķiras sportista un lidaparāta lineārais ātrums – 1 punkts.
4. Vērtē līmeņos:
skaidro smaguma spēka izmaiņas, mainoties lidaparāta augstumam virs Zemes – 2 punkti;
skaidrojumā pieļautas nelielas neprecizitātes – 1 punkts;
skaidrojums nepilnīgs – 0 punkti.
5. Vērtē līmeņos:
uzraksta un pamato divus apstākļus vai lidojuma īpatnības, kas var ietekmēt baterijas darbības laiku – 2 punkti;
uzraksta un pamato vienu apstākli vai lidojuma īpatnību, kas var ietekmēt baterijas darbības laiku – 1 punkts;
uzraksta apstākli vai lidojuma īpatnību, kas var ietekmēt baterijas darbības laiku, bet nepamato – 0 punkti.