Uz nelielas kvēlspuldzes uzrakstīts: \(6\space\mathrm V\) un \(0,3\space\mathrm A\). Izmantojot Oma likumu, iespējams izrēķināt, ka kvēlspuldzes pretestība ir \(20\space \Omega\). Brīdī, kad kvēlspuldze nav pieslēgta spriegumam, ar ommetru izmērīja, ka kvēlspuldzes pretestība ir \(2,3\space\Omega\). Lai saprastu, cik liela īsti ir kvēlspuldzes pretestība, izveidoja shēmu, kas sastāv no baterijas, kvēlspuldzes un reostata. Baterijas iekšējā pretestība ir nenozīmīgi maza.
1. Pabeidz zīmēt elektrisko shēmu un iezīmē tajā ampērmetru un voltmetru tā, lai varētu izmērīt spuldzē plūstošās strāvas stiprumu un spriegumu uz tās!
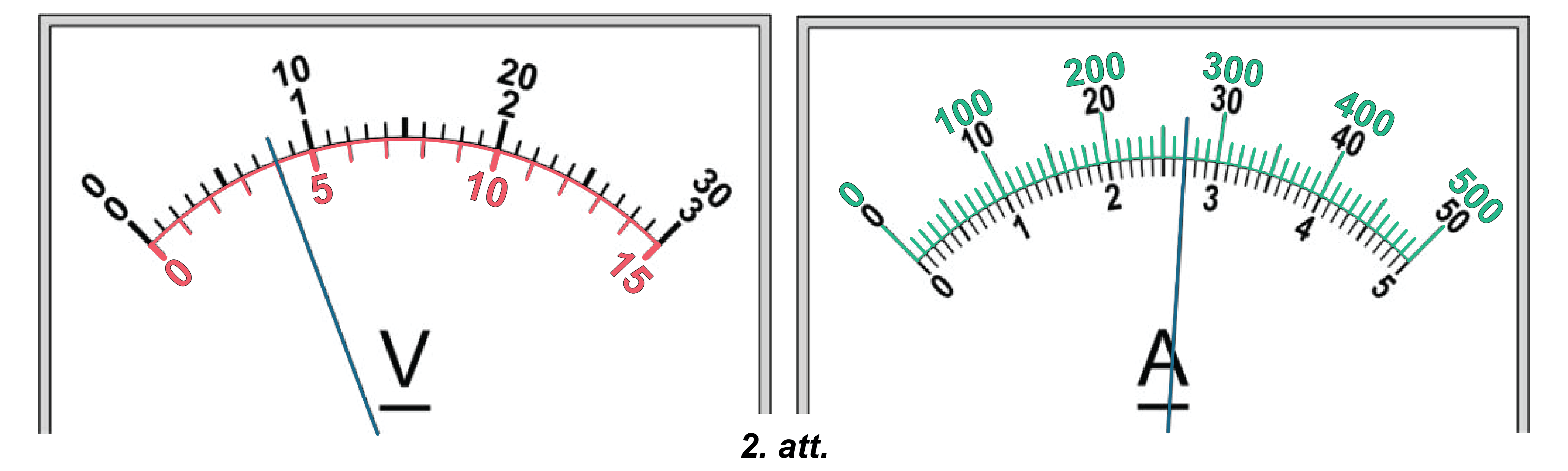
2. Zināms, ka voltmetra mērīšanas diapazons slēgumā ir \(15\space\mathrm V\), bet ampērmetra mērīšanas diapazons ir \(500\space\mathrm {mA}\).
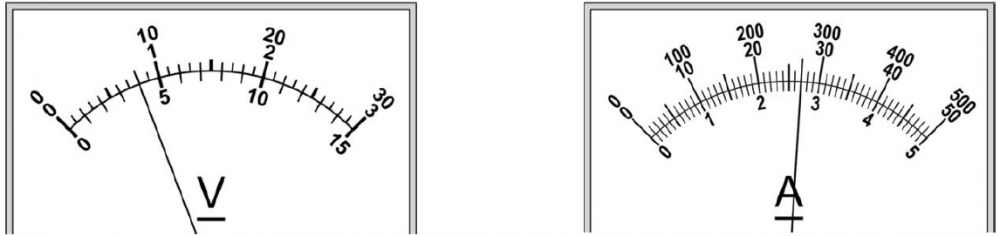
Nolasi voltmetra un ampērmetra rādījumus!
3. Nosaki attēlā redzamā sprieguma mērījuma relatīvo kļūdu, ja par absolūto kļūdu pieņem pusi no mēraparāta mazākās iedaļas vērtības!
4. Eksperimenta rezultātus attēloja grafikā.
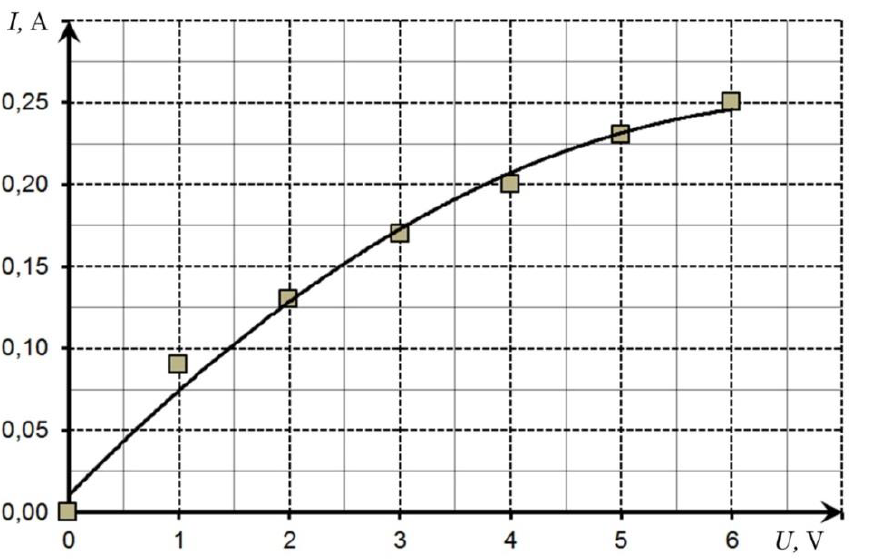
Pēc grafika nosaki, kā mainās kvēlspuldzes pretestība atkarībā no sprieguma!
5. Šobrīd kvēlspuldzes pamazām aizstāj ar gaismas diodēm. Kādas pretestības rezistors jāieslēdz virknē ar gaismas diodi, kurai uz iepakojuma rakstīts \(2,5\space\mathrm V\) un \(200\space\mathrm {mA}\), ja strāvas avota spriegums ir \(6\space\mathrm V\)?
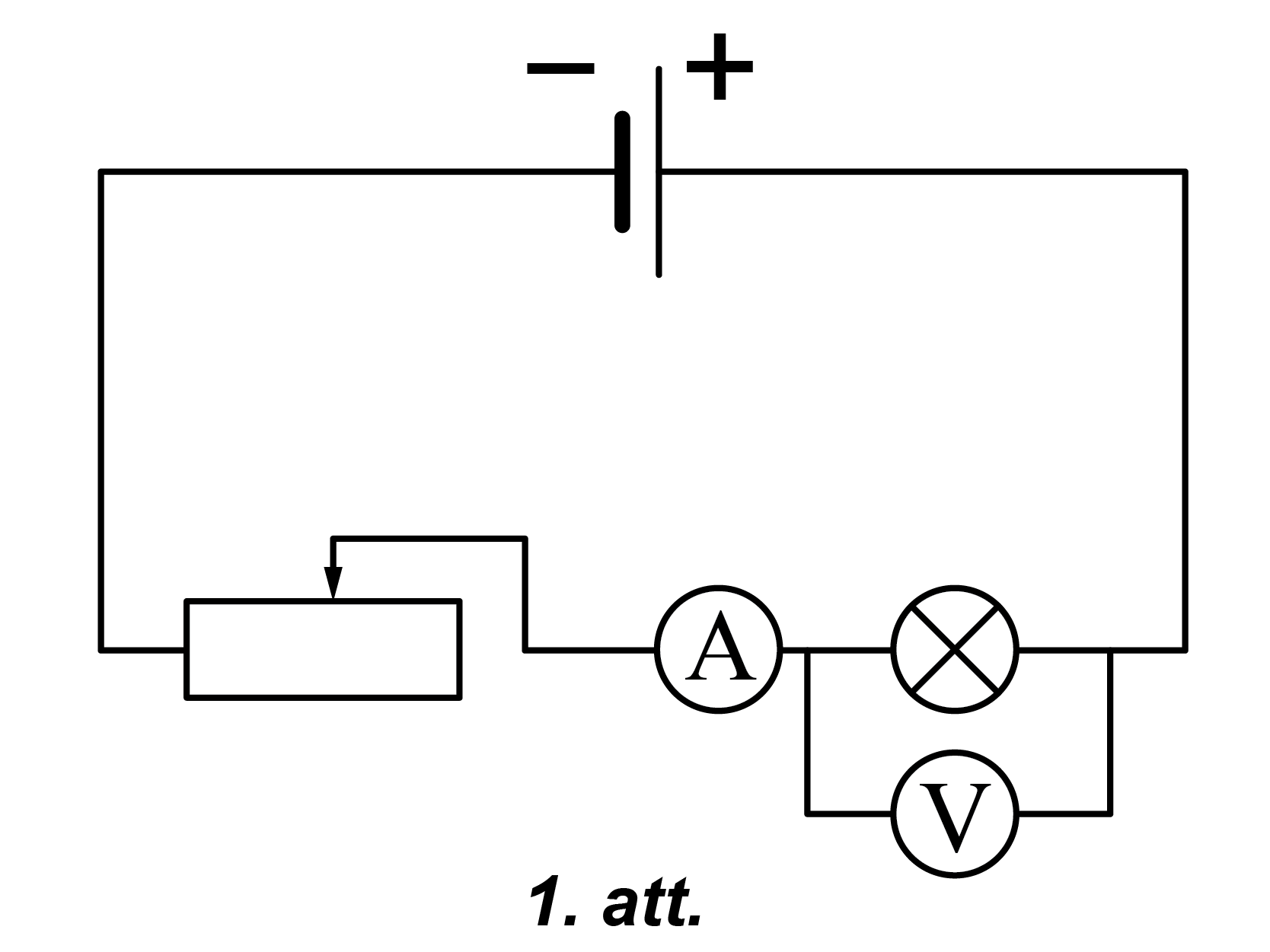
1. Strāvas stiprumu ķēdē mēra ar ampērmetru, kuru slēdz virknē ar spuldzi. Spriegumu mēra ar voltmetru, kuru slēdz paralēli spuldzei, kā parādīts zīmējumā (skatīt 1. attēlu). Ieslēdzot ampērmetru un voltmetru līdzstrāvas ķēdē, ir jāievēro polaritāte.
2. Mērierīču skalas ir parādītas zīmējumā (skatīt 2. attēlu). Katrai mērierīcei ir trīs mērīšanas diapazoni. Voltmetra skalas iedaļas vērtība ir \(1\space\mathrm V\). Ampērmetra skalas iedaļas vērtība ir \(10\space\mathrm{mA}\).
Voltmetra rādījums ir \(4\space\mathrm V\). Ampērmetra rādījums \(270\space\mathrm{mA}\).
3. Mērījuma relatīvo kļūdu \(r\) aprēķina pēc formulas \(r=\frac{\Delta U}{U}\cdot100\%\), kur \(U\) ir izmērītais spriegums, \(\Delta U\) – mērījuma absolūtā kļūda, kas vienāda ar pusi no iedaļas vērtības (pēc uzdevuma tekstā sniegtās informācijas). Tāpēc \(U=4,0\space\mathrm V\), bet \(\Delta U=0,5\space\mathrm V\).
Aprēķini: \(r=\frac{\Delta U}{U}\cdot100\%=\frac{0,5}{4,0}\cdot100\%\approx13\space\%\).
Atbilde: mērījuma relatīvā kļūda ir aptuveni \(13\space\%\).
4. No grafika aprēķina spuldzes pretestību punktos B, C un D (skatīt 3. attēlu). No Oma likuma ķēdes posmam \(I=\frac{U}{R}\) izsaka pretestību \(R=\frac{U}{I}\) un aprēķina pretestību norādītajos punktos:
\(R_\mathrm B=\frac{U}{I}=\frac{1,0}{0,075}\approx13\space\Omega\);
\(R_\mathrm C=\frac{U}{I}=\frac{2,5}{0,150}\approx17\space\Omega\);
\(R_\mathrm D=\frac{U}{I}=\frac{5,0}{0,230}\approx22\space\Omega\).
Ir redzams, ka, paaugstinoties spriegumam uz spuldzes, tās pretestība palielinās.

5.
1. variants
Uzzīmē shēmu, balstoties uz uzdevuma teksta. Shēmā pieraksta lielumus, kuru vērtība ir zināma:
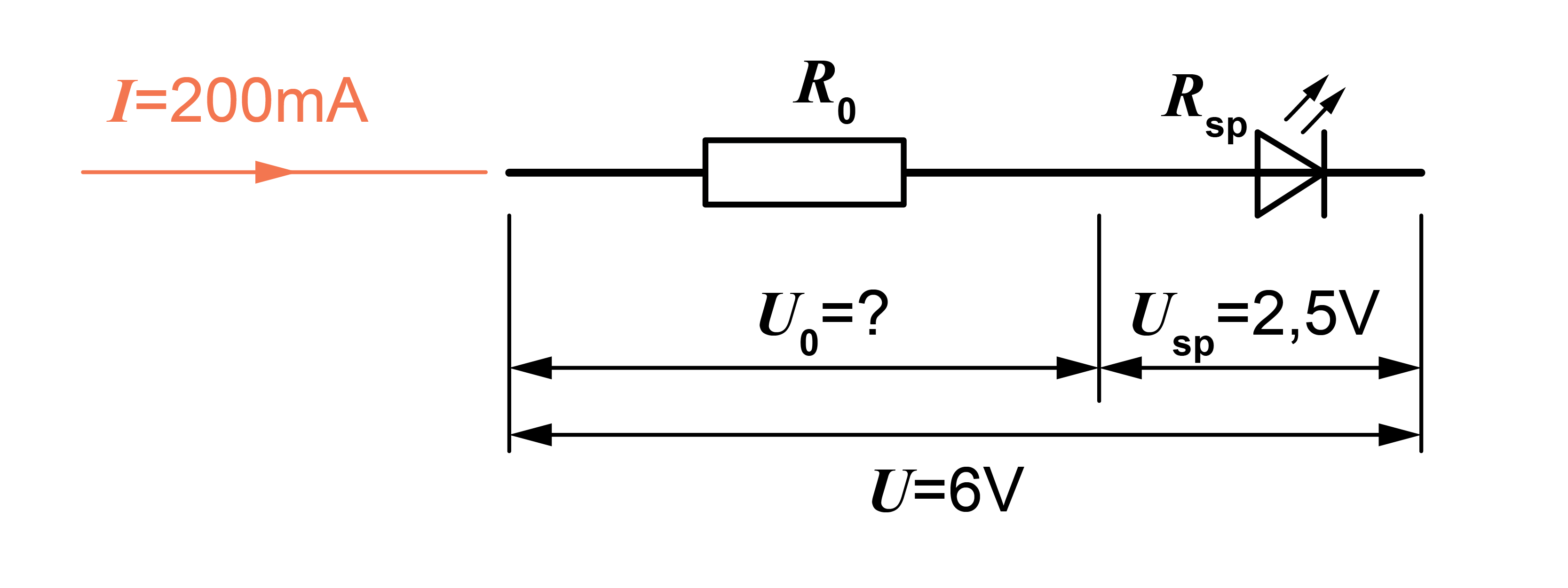
Virknes slēgumā kopējais spriegums ir atsevišķo posmu spriegumu kritumu summa: \(U=U_0+U_\mathrm{sp}\), kur \(U_0\) ir spriegums uz rezistora. Aprēķina spriegumu uz rezistora: \(U_0=U-U_\mathrm{sp}=6-2,5=3,5\space\mathrm V\).
Virknes slēgumā visos patērētājos strāvas stiprums ir vienāds, tāpēc arī rezistorā plūst \(I=200\space\mathrm{mA}=0,2\space\mathrm A\). Aprēķina rezistora pretestību pēc Oma likuma ķēdes posmam \(I=\frac{U_0}{R_0}\). Izsaka meklējamo lielumu un veic aprēķinus: \(R_0=\frac{U_0}{I}=\frac{3,5}{0,2}=17,5\space\mathrm A\).
2. variants
Rezistors, spuldze un strāvas avots veido virknes slēgumu (skatīt 4. attēlu).
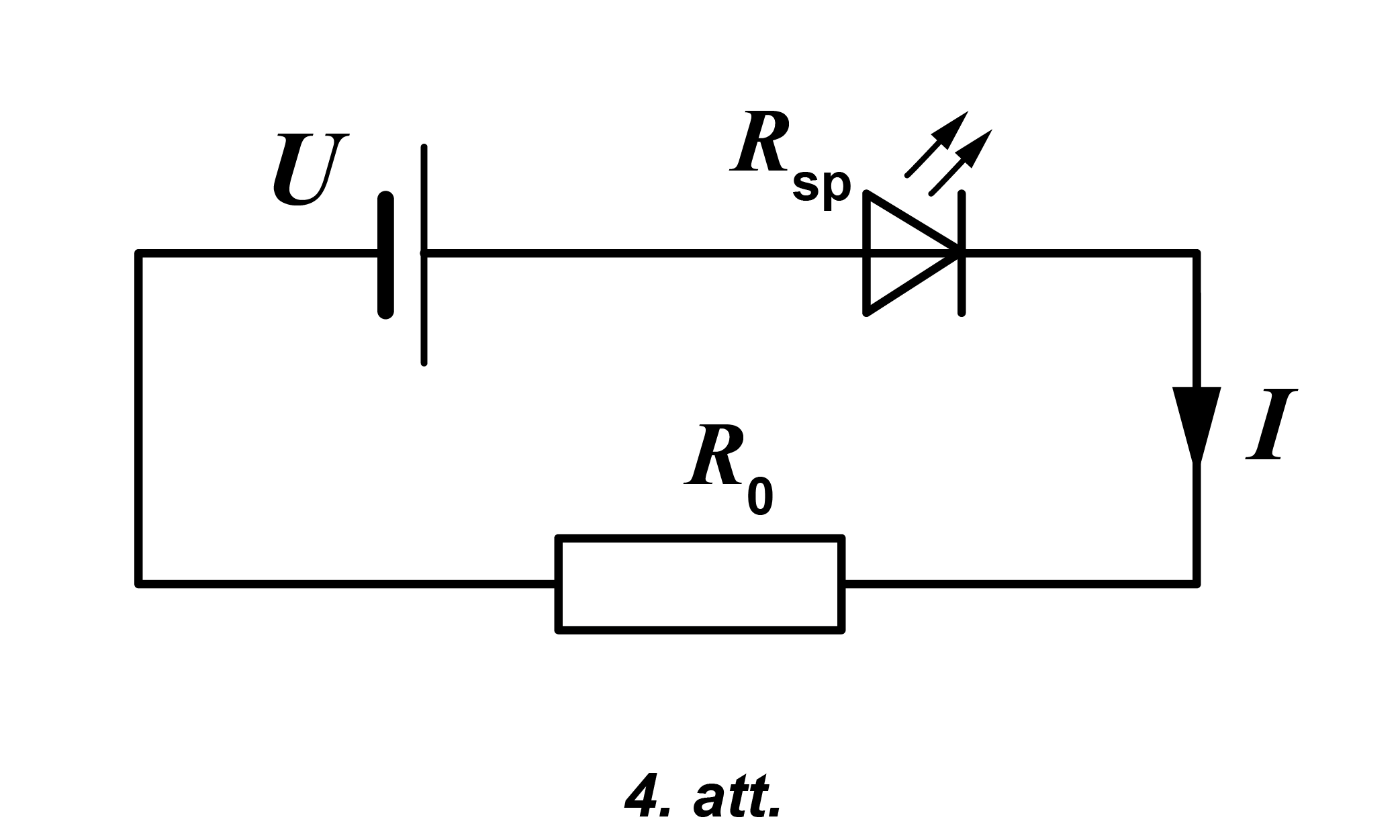
Pielieto Oma likuma formulu pilnai ķēdei \(I=\frac{\mathscr E}{R+r}\), kur \(R\) – ārējās ķēdes kopējā pretestība. Strāvas avota EDS uzdevumā nosaukts kā strāvas avota spriegums \(U\). Ārējā ķēde sastāv no rezistora un spuldzes. Tādēļ \(R=R_0+R_\mathrm{sp}\). Strāvas avota iekšējā pretestība ir vienāda ar nulli. Ievieto ķēdes ārējo pretestību Oma likuma formulā un iegūst \(I=\frac{U}{R_0+R_\mathrm{sp}}\). Tālāk var rēķināt dažādi:
A paņēmiens
No formulas \(I=\frac{U}{R_0+R_\mathrm{sp}}\) izsaka spriegumu: \(U=I(R_0+R_\mathrm{sp})=IR_0+IR_\mathrm{sp}\). Izteiksme \(IR_\mathrm{sp}\) ir spriegums starp spuldzītes spailēm \(U_\mathrm{sp}=2,5\space\mathrm V\). Tādēļ formulai ir cits pieraksts: \(U=IR_0+U_\mathrm{sp}\). No formulas izsaka rezistora pretestību un veic aprēķinus: \(R_0=\frac{U-U_\mathrm{sp}}{I}\frac{6,0-2,5}{0,2}=17,5\space\Omega\approx18\space\Omega\).
B paņēmiens
No formulas \(I=\frac{U}{R_0+R_\mathrm{sp}}\) izsaka rezistora pretestību \(R_0=\frac{U}{I}-R_\mathrm{sp}\). Nav zināma spuldzītes pretestība \(R_\mathrm{sp}\). Spuldzītes pretestību nosaka no Oma likuma ķēdes posmam formulas \(I=\frac{U_\mathrm{sp}}{R_\mathrm{sp}}\), kur \(U_\mathrm{sp}=2,5\space\mathrm V\) un \(I=0,2\space\mathrm A\). Spuldzītes pretestība \(R_\mathrm{sp}=\frac{U_\mathrm {sp}}{I}\).
Aprēķini: \(R_\mathrm{sp}=\frac{U_\mathrm {sp}}{I}=\frac{2,5}{0,2}=12,5\space\Omega\)
\(R_0=\frac{U}{I}-R_\mathrm{sp}=\frac{6,0}{0,2}-12,5=17,5\space\Omega\approx18\space\Omega\).
Atbilde: rezistora pretestība aptuveni \(18\space\Omega\).
Vērtēšanas kritēriji
1. Iezīmē shēmā ampērmetru un voltmetru – 1 punkts.
2. Nolasa voltmetra un ampērmetra rādījumus – 1 punkts.
3. No uzdevuma teksta nosaka sprieguma mērījuma absolūtās kļūdas skaitlisko vērtību – 1 punkts.
Aprēķina sprieguma mērījuma relatīvo kļūdu – 1 punkts.
4. No grafika nosaka, kā mainās kvēlspuldzes pretestība atkarībā no sprieguma – 1 punkts.
Pamato atbildi ar aprēķiniem vai loģiskiem spriedumiem – 1 punkts.
5.
1. variants
Zīmē shēmu un pieraksta shēmā apzīmējumus un zināmos lielumus. Lieto virknes slēguma likumsakarības – 1 punkts.
Zina vai atrod formulu lapā Oma likumu ķēdes posmam. Saskaņo mērvienības un aprēķina nezināmo pretestību – 1 punkts.
2. variants
Uzzīmē shēmu pēc uzdevuma teksta. Zina vai atrod formulu lapā Oma likumu noslēgtai ķēdei – 1 punkts.
Zina vai atrod formulu lapā Oma likumu ķēdes posmam. Saskaņo mērvienības un aprēķina nezināmo pretestību – 1 punkts.