Autoskolas mašīna aprīkota ar sensoriem, lai mērītu gaisa spiedienu un temperatūru riepās. Riepas tilpums ir 110 litri. Brauciena sākumā spiediens riepā ir 320 kPa un temperatūra ir 18 °C.
1. Aprēķini, cik molu gaisa ir riepā!
2. Brauciena laikā gaisa temperatūra riepā pieauga līdz 54 °C. Aprēķini riepā esošā gaisa iekšējās enerģijas izmaiņu, pieņemot, ka gaisu var uzskatīt par divatomu gāzi! Parādi risinājuma gaitu!
3. Nosaki, cik lielu siltuma daudzumu sasilstot saņēma gaiss automašīnas riepā! Pamato savu spriedumu, izmantojot pirmo termodinamikas likumu!
4. No drošības viedokļa būtisks raksturlielums ir riepu saskares laukums ar ceļu. Kā un par cik izmainītos riepas saskares laukums ar ceļu, ja temperatūras pieauguma rezultātā spiediens riepā sasniegtu 370 kPa? Automašīnas masa ir 1200 kg.
1. punkts
Uzdevumā dots gāzes tilpums \(V\), gāzes spiediens \(p\) un gāzes temperatūra \(T\). Jāaprēķina vielas daudzums \(n\).
Šos lielumus savā starpā saista datu bukletā atrodamais Klapeirona–Mendeļejeva vienādojums (ideālas gāzes stāvokļa vienādojums): \(pV=nRT\).
No šīs sakarības jāizsaka vielas daudzums un jāievieto skaitliskās vērtības SI pamatvienībās.
\(T=273+18=291\space\mathrm{K}\); \(V=110\cdot10^{-3}\space\mathrm{m^3}=0{,}110\space\mathrm{m^3}\), \(p=320\cdot10^3\space\mathrm{Pa}\).
\(pV=nRT\space\implies\space n=\frac{pV}{RT}=\frac{320\cdot10^3\cdot0,110}{8,31\cdot 291}\approx14{,}6\space\mathrm{mol}\)
Atbilde: riepā ir \(14{,}6\space\mathrm{mol}\) gaisa.
2. punkts
Lai aprēķinātu riepā esošā gaisa iekšējās enerģijas izmaiņu, jāizmanto datu bukletā atrodama gāzes iekšējās enerģijas aprēķina formula: \(U=\frac{i}{2}nRT\).
Jāatceras arī, ka divatomu gāzes gadījumā molekulu kustības brīvības pakāpju skaits \(i\) ir \(5\).
(Par gāzes iekšējo enerģiju un molekulu kustības brīvības pakāpēm var uzzināt Fizmix portālā: https://www.fizmix.lv/fiztemas/siltums-un-darbs-9/iekseja-energija)
Iekšējās enerģijas izmaiņa \(\Delta U=U_2-U_1=\frac{i}{2}nR(T_2-T_1)=\frac{i}{2}nR\Delta T=\frac{5\cdot14{,}6\cdot8{,}31\cdot36}{2}\approx10{,}920\space\mathrm{J}\).
Atbilde: gaisa iekšējās enerģijas izmaiņa ir \(10{,}920\space\mathrm{J}\).
3. punkts
Pirmais termodinamikas likums ir atrodams datu bukletā: \(\Delta U=Q-A\). Pirmais termodinamikas likums ir enerģijas nezūdamības likums. Pirmais termodinamikas likums nosaka, ka siltumapmaiņas procesā termodinamiskai sistēmai pievadītais siltuma daudzums tiek patērēts sistēmas iekšējās enerģijas izmaiņai un/vai mehāniskā darba veikšanai. Piemēram, gāze veic darbu, izobāriski izplešoties: \(A=p\Delta V\).
Ja darbs netiek veikts, viss gāzei pievadītais siltuma daudzums \(Q\) tiek patērēts tās iekšējās enerģijas palielināšanai par \(\Delta U\).
Uzdevumā aprakstītajā situācijā darbs netiek veikts, jo riepas tilpums nemainās. Tātad \(\Delta V=0\) un \(A=0\).
Gaisam pievadītais siltuma daudzums vienāds ar tā iekšējās enerģijas izmaiņu, kas aprēķināta uzdevuma 2. punktā:
\(Q=\Delta U=10920\space\mathrm{J}\).
Atbilde: gaiss automašīnas riepā saņēma \(10920\space\mathrm{J}\) lielu siltuma daudzumu.
4. punkts
Saskares vietā ar ceļu spiedienam uz riepu no iekšpuses un no ārpuses jābūt vienādam. No ārpuses darbojas balsta reakcijas spēks, kas vienāds ar automašīnas svaru, tātad – spiedienam riepās jābūt vienādam ar automašīnas radīto spiedienu uz ceļu.
Pieaugot spiedienam riepās, to saskares laukumam ar ceļu jāsamazinās, jo spiediena spēks uz ceļu ir nemainīgs (vienāds ar mašīnas svaru).
Saskares laukums pie sākotnējā spiediena: \(S_1=\frac{mg}{p_1}=\frac{1200\cdot10}{3{,}2\cdot10^5}=3{,}75\cdot10^{-2}\space\mathrm{m^{2}}\).
Saskares laukums pēc temperatūras pieauguma: \(S_2=\frac{mg}{p_2}=\frac{1200\cdot10}{3{,}7\cdot10^5}=3{,}24\cdot10^{-2}\space\mathrm{m^{2}}\).
Riepu saskares laukuma izmaiņa (visiem automobiļa riteņiem kopā) \(\Delta S=S_1-S_2=3{,}75\cdot10^{-2}-3{,}24\cdot10^{-2}=0{,}51\cdot10^{-2}=5{,}1\cdot10^{-3}\space\mathrm{m^2}=51\space\mathrm{cm^2}\).
Uzdevumā nav dots automašīnas riteņu skaits, tāpēc pieņem arī atbildes, kuras tika iegūtas, doto laukuma izmaiņu dalot ar jebkuru riteņu skaitu (piemēram, ar \(4\)).
Piezīme: tā kā uzdevumā nav norādīta mērvienība, ar kādu sniedzama atbilde, pareiza ir arī procentos izteikta atbilde.
\(\frac{S_2}{S_1}=\frac{mg}{p_2}:\frac{mg}{p_1}=\frac{mgp_1}{mgp_2}=\frac{p_1}{p_2}=\frac{3{,}24}{3{,}75}=0{,}864\).
Riepas laukums pēc temperatūras paaugstināšanās ir \(86{,}4\%\) no sākotnējā. Tātad riepas laukums samazinājies par \(13{,}5\%\).
Atbilde: temperatūras pieauguma rezultātā riepas saskares laukums ar ceļu samazinājies par \(51\space\mathrm{cm^2}\) (visiem riteņiem kopā).
1. punkts
Uzdevuma izpilde eksāmenā – 60,8%.
Vērtēšanas kritēriji
Ir risinājuma gaita gaisa daudzuma aprēķināšanai (formula \(pV=nRT\) un/vai formulā ievietoti skaitļi) – 1 punkts.
Pareizs aprēķins ar mērvienību (ja nav redzama risinājuma gaita, punktu neieskaita). Pieļaujama viena neliela kļūda aprēķinā. Ja izmantota Celsija temperatūra un/vai tilpums litros, punktu neieskaita – 1 punkts.
Zīmīgo ciparu skaitu atrisinājumā nevērtē.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.

2. piemērs: risinājums novērtēts ar 2 punktiem. Pieļauta neuzmanības kļūda, ievietojot molārās gāzu konstantes \(R\) vērtību.
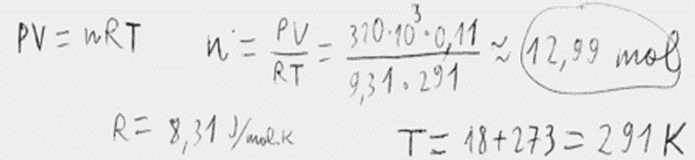
3. piemērs: risinājums novērtēts ar 1 punktu. Vielas daudzums \(n\) nepareizi izteikts no formulas.
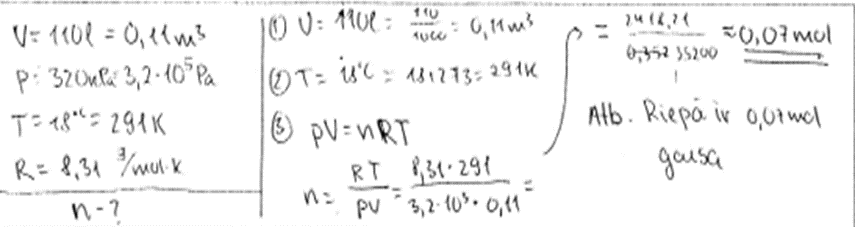
4. piemērs: risinājums novērtēts ar 1 punktu. Mērvienības nav pārveidotas, kļūdas aprēķinā.
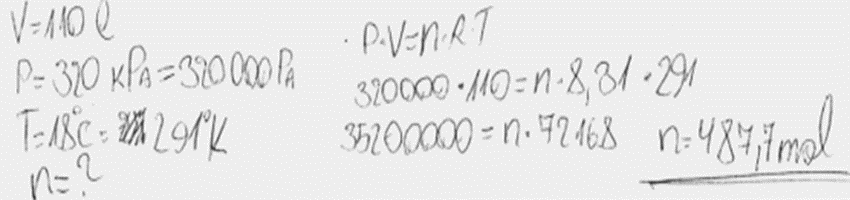
5. piemērs: risinājums novērtēts ar 0 punktu. Nav parādīta risinājuma gaita.
![]()
2. punkts
Uzdevuma izpilde eksāmenā – 41,9%.
Vērtēšanas kritēriji
Zina, ka divatomu gāzes gadījumā molekulu kustības brīvības pakāpju skaits \(i=5\) – 1 punkts. Punktu ieskaita arī tad, ja uzrakstīta nepareiza iekšējās enerģijas izmaiņas \(\Delta U\) aprēķināšanas formula. Var nebūt rakstīts brīvības pakāpju skaita apzīmējums "\(i\)\(i\)", bet saprotams no risinājuma.
Aprēķināta iekšējās enerģijas izmaiņa \(\Delta U\) , izmantojot formulu \(\Delta U=\frac{i}{2}nR\Delta T\) (formula un/vai formulā ievietoti skaitļi), rezultāts ir pierakstīts ar mērvienību – 1 punkts. Punktu ieskaita arī tad, ja izmantota cita brīvības pakāpju skaita \(i\) vērtība. Pieļaujama viena neliela kļūda aprēķinā. Aprēķinā izmanto uzdevuma 1. punktā iegūto vielas daudzuma \(n\) vērtību.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.

2. piemērs: risinājums novērtēts ar 2 punktiem.

3. piemērs: risinājums novērtēts ar 1 punktu. Pieņemts, ka gāzes brīvības pakāpju skaits \(i=3\).
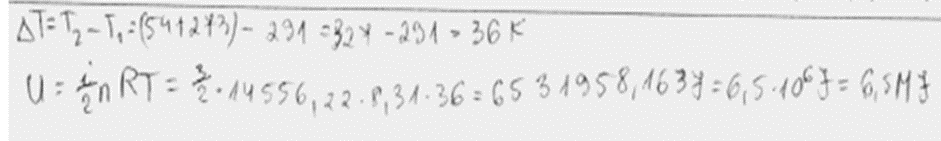
4. piemērs: risinājums novērtēts ar 1 punktu. Ir pareizs brīvības pakāpju skaits. Nav rēķināta iekšējās enerģijas izmaiņa, nav aprēķināts vielas daudzums.

5. piemērs: risinājums novērtēts ar 0 punktu. Pieņemts, ka gāzes brīvības pakāpju skaits \(i=3\). Temperatūras izmaiņai \(\Delta T\) pieskaitīts \(273\).
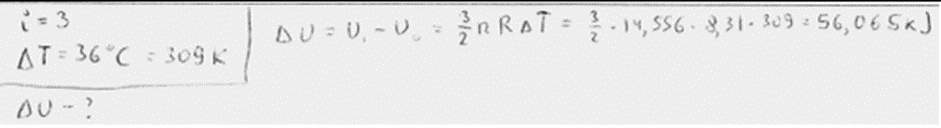
3. punkts
Uzdevuma izpilde eksāmenā – 44,7%.
Vērtēšanas kritēriji
Uzraksta Pirmo termodinamikas likumu ar formulu vai ar vārdiem (demostrējot izpratni, ka tas ir enerģijas nezūdamības likums) – 1 punkts.
Secināts, ka saņemtais siltuma daudzums \(Q=\Delta U=10920\space\mathrm{J}\) (vai cita iepriekšējā uzdevuma punktā iegūtā vērtība.) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
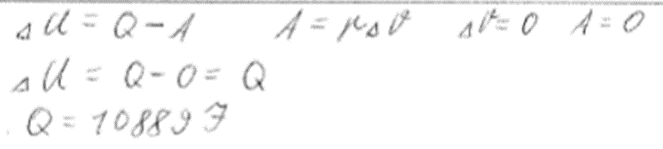
2. piemērs: risinājums novērtēts ar 2 punktiem. Rezultāts atbilst iepriekšējā uzdevuma punktā iegūtai vērtībai.

3. piemērs: risinājums novērtēts ar 1 punktu. Ir uzrakstīts Pirmais termodinamikas likums, bet nav izpratnes par to, ka aplūkotajā procesā netiek veikts darbs.

4. piemērs: risinājums novērtēts ar 0 punktu. Risinājuma nav, skaitliskā vērtība neatbilst iepriekšējā uzdevuma punktā iegūtai iekšējās enerģijas izmaiņas vērtībai.

4. punkts
Uzdevuma izpilde eksāmenā – 23,2%.
Vērtēšanas kritēriji
Pamatots spriedums, ka temperatūras pieauguma rezultātā saskares laukumam jāsamazinās – 1 punkts.
Ir risinājuma gaita saskares laukuma aprēķināšanai (formula \(S=\frac{mg}{p}\) un/vai formulās ievietoti skaitļi) – 1 punkts.
Pareizs laukumu aprēķins ar mērvienībām – 1 punkts. Ja nav redzama risinājuma gaita, punktu neieskaita. Pieļaujama viena kļūda aprēķinā.
Aprēķināta saskares laukuma izmaiņa – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem.

2. piemērs: risinājums novērtēts ar 4 punktiem.

3. piemērs: risinājums novērtēts ar 4 punktiem. Viena neuzmanības kļūda (\(12\) dalot ar \(4\), skolēns iegūst \(4\)).

4. piemērs: risinājums novērtēts ar 3 punktiem. Nepareizs saskares laukuma izmaiņas aprēķins.
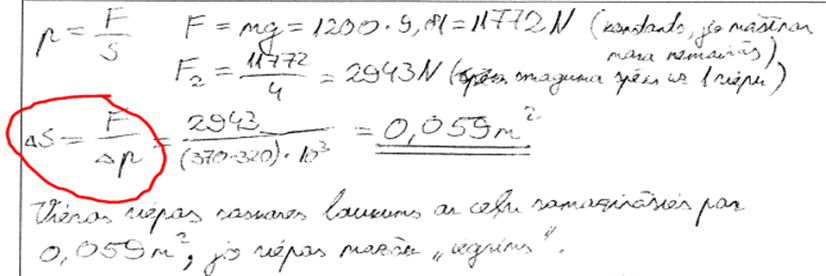
5. piemērs: risinājums novērtēts ar 3 punktiem. Rēķināta laukumu attiecība, tādā veidā sniedzot atbildi uz jautājumu "cik reižu", nevis "par cik".
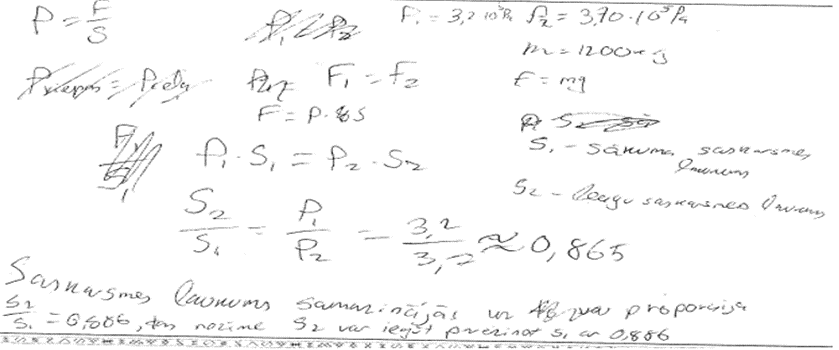
6. piemērs: risinājums novērtēts ar 2 punktiem. Saprasts, kā rēķināt laukumu un ka jāaprēķina starpība.

7. piemērs: risinājums novērtēts ar 1 punktu. Saprasts, kā rēķināt laukumu.
