Skolēns, pētot difrakcijas parādību, izmantoja gaismas diodi, kura var izstarot gaismu ar trim dažādiem viļņa garumiem.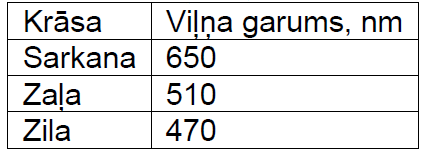
Izmantojot fizikas kabinetā esošos optiskos instrumentus, viņš ieguva šauru gaismas kūli, kura ceļā novietoja difrakcijas režģi. Aiz režģa \(2,5\space\mathrm m\) lielā attālumā novietoja ekrānu un ieslēdza diodi tā, ka tā izstaroja tikai zilo gaismu.
Skolēns izmērīja attālumu no centrālā maksimuma līdz otrās kārtas maksimumam un ieguva mērījumu \(7,8\space\mathrm {cm}\). Pēc tam skolēns izrēķināja, ka otrās kārtas maksimums attiecībā pret centrālo maksimumu novirzīts par \(1,8^\mathrm o\) lielu leņķi.
1. Uzraksti formulu, kuru izmantojot, var aprēķināt difrakcijas režģa konstanti, un pieraksti formulā zināmo lielumu skaitliskās vērtības un mērvienības!
2. Diodi elektriskajā ķēdē ieslēdza tā, ka tā izstaro visu trīs krāsu gaismas. Kādā secībā novērojamas spektra pirmās kārtas krāsas, sākot ar tuvāko centrālajam maksimumam?
3. Lai diode izstarotu sarkano gaismu, tā jāpieslēdz \(2\space\mathrm V\) spriegumam. Lai diode izstarotu zilo gaismu, tā jāpieslēdz \(4\space\mathrm V\) spriegumam, jo zilās gaismas fotonu enerģija ir lielāka nekā sarkanās gaismas. Izmantojot fizikas formulas un uzdevumā doto tabulu, pierādi, ka zilās gaismas fotonu enerģija ir lielāka par sarkanās gaismas fotonu enerģiju!
4. Digitālā fotoaparāta galvenās sastāvdaļas ir gaismjutīga lādiņsaites matrica, objektīvs, zibspuldze, procesors un atmiņas karte. Kā un kāpēc, izmantojot interferences parādību, ir uzlabota viena no iepriekš minētajām fotoaparāta sastāvdaļām?
1. Difrakcijas režģa konstanti \(d\) nosaka pēc formulas \(d\sin\varphi=k\lambda\), kur \(\varphi\) – difrakcijas leņķis, \(k\) – difrakcijas spektra (maksimuma) kārta, \(\lambda\) – starojuma viļņa garums. Uzdevumā doti sekojošās lielumu skaitliskās vērtības: \(\varphi=1,8^\mathrm o,\space k=2,\space\lambda=470\space\mathrm{nm}=4,7\cdot10^{-7}\space\mathrm m\).
2. Tā kā difrakcijas režģa konstante \(d\) un spektra kārta \(k\) nemainās, tad no difrakcijas režģa formulas \(d\sin\varphi=k\lambda\) secina, ka \(\sin\varphi\sim\lambda\). Pirmajā kvadrantā sinusa funkcija ir augoša, tātad, jo lielāks ir viļņa garums \(\lambda\), jo lielāks ir arī difrakcijas leņķis \(\varphi\).
Uzdevumā ir doti starojumi ar trim dažādiem viļņa garumiem. Sakarība starp viļņu garumiem ir sekojoša: \(\lambda_{\mathrm{sarkana}}>\lambda_{\mathrm{zaļa}}>\lambda_{\mathrm{zila}}\). Tādēļ \(\varphi_{\mathrm{sarkana}}>\varphi_{\mathrm{zaļa}}>\varphi_{\mathrm{zila}}\) un pirmās kārtas spektru krāsas, skatot no centrālā maksimuma, ir sekojoša: zila, zaļa, sarkana.
3. Elektromagnētiskā starojuma kvanta enerģiju \(W\) nosaka pēc formulas \(W=hf\), kur \(h\) – Planka konstante, \(f\) – elektromagnētiskā viļņa frekvence.
Elektromagnētiskā viļņa garumu \(\lambda\) nosaka pēc formulas \(\lambda=cT\) vai \(\lambda=\frac{c}{f}\), kur \(T\) – viļņa periods, \(c\) – elektromagnētisko viļņu izplatīšanās ātrums vakuumā. No pēdējās formulas izsakot \(f=\frac{c}{\lambda}\) un ievietojot kvanta enerģijas formulā, iegūst \(W=\frac{hc}{\lambda}\).
Skaidrojums un aprēķini:
1. variants (skaidrojums, neveicot aprēķinus)
Formulā \(W=\frac{hc}{\lambda}\) Planka konstante \(h\) un gaismas ātrums \(c\) ir nemainīgi lielumi. Mainīgie lielumi – viļņa garums \(\lambda\) un kvanta enerģija \(W\) – ir apgriezti proporcionāli lielumi. Tas nozīmē, ka, jo mazāks ir elektromagnētiskā starojuma viļņa garums, jo lielāka ir kvanta enerģija. Tāpēc zilās gaismas kvanta enerģija ir lielāka nekā sarkanās gaismas kvanta enerģija.
2. variants (aprēkinot katra kvanta enerģiju)
\(W_\mathrm{zila}=\frac{hc}{\lambda\mathrm{zila}}=\frac{6,63\cdot10^{-34}\cdot3\cdot10^8}{470\cdot10^{-9}}\approx4,23\cdot10^{-19}\space\mathrm J\).
\(W_\mathrm{sarkana}=\frac{hc}{\lambda\mathrm{sarkana}}=\frac{6,63\cdot10^{-34}\cdot3\cdot10^8}{650\cdot10^{-9}}\approx3,06\cdot10^{-19}\space\mathrm J\).
Pēc aprēķiniem ir redzams, ka \(W_\mathrm{zila}>W_\mathrm{sarkana}\).
4. Interferences parādību izmanto fotoaparāta objektīva caurspīdības uzlabošanai.
Objektīvs ir lēca vai lēcu kopums, caur kuru gaismas kūlis nokļūst līdz gaismjūtīgajai lādiņsaites matricai. Taču no katras lēcas virsmas gaisma daļēji atstarojas, un matricas virsmas apgaismojums samazinās.
Lai samazinātu atstarotās gaismas enerģiju, uz lēcas virsmas uzklāj plānu caurspīdīgas vielas kārtiņu, kurai ir no lēcas materiāla atšķirīgs gaismas laušanas koeficients. Gaisma atstarojas no abām kārtiņas virsmām. Pārklājuma biezums ir izvēlēts tāds, lai abiem atstarotajiem gaismas viļņiem būtu pretējas fāzes. Tad viļņi, interferējot, viens otru dzēš, un matricas virsmas apgaismojums palielinās.
Tomēr dzidrinošā kārtiņa nevar novērst visas gaismas atstarošanos, jo tajā gaismas interferences minimuma nosacījums izpildās tikai noteiktam viļņa garumam. Rezultātā – atstarotajā gaismā pazūd viena no spektrālajām krāsām.
Vērtēšanas kritēriji
1. Zina vai atrod formulu lapā difrakcijas režģa formulu un pieraksta formulā zināmo lielumu skaitliskās vērtības un mērvienības – 1 punkts.
2. No difrakcijas režģa formulas nosaka sakarību starp difrakcijas leņķa sinusu un viļņa garumu – 1 punkts.
Nosaka kādā secībā novērojamas spektra pirmās kārtas krāsas – 1 punkts.
3. No fizikas formulu lapā atrodamajām formulām, izveido jaunu formulu, kas saista kvanta enerģiju un viļņa garumu – 1 punkts.
Izmanto uzdevumā doto informāciju un izdara secinājumu par gaismas kvanta enerģiju – 1 punkts.
4. Zina, kāpēc interferenci izmanto optisko materiālu dzidrināšanā – 1 punkts.
Skaidro, kā panāk, ka no fotoaparāta lēcas daļa gaismas netiek atstarota – 1 punkts.