Gaismas avots sastāv no diviem lāzeriem, kas vienlaikus staro gaismu ar diviem dažādiem gaismas viļņu garumiem. Viena gaismas viļņa garums ir 628 nm, otrs – īsāks, bet nezināms. Gaismas avota gaismu pēta, izmantojot difrakcijas režģi un ekrānu. Zīmējumā mērogs nav ievērots.
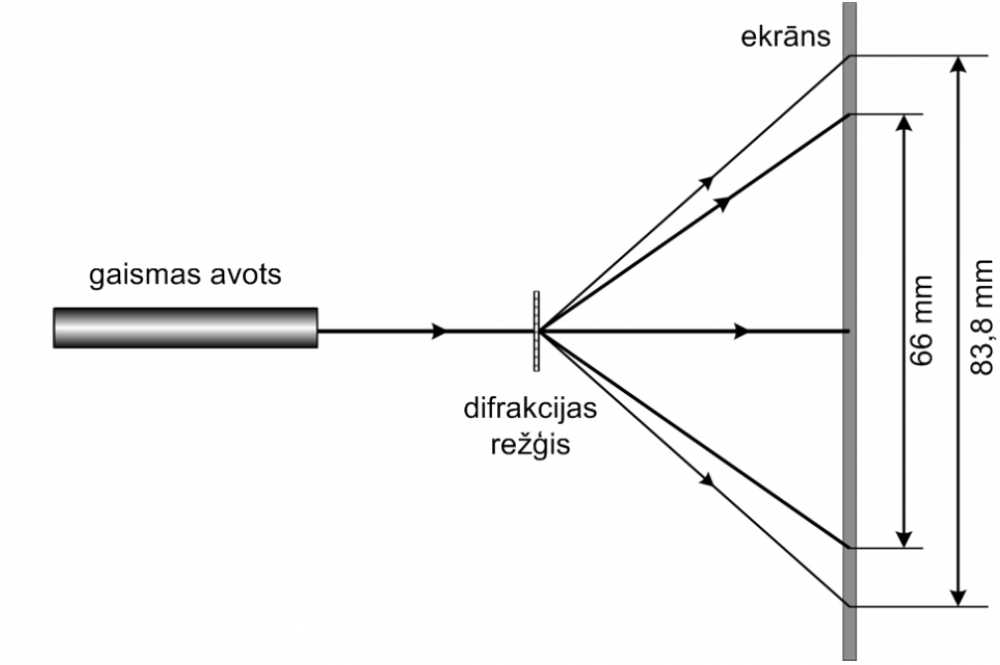
Uz ekrāna novēro piecus difrakcijas attēlus, no kuriem četri ir pirmās kārtas spektra attēli. Informācija par režģa konstantes lielumu nav dota. Attālums no režģa līdz ekrānam ir 78,5 mm. Cik liels ir nezināmā gaismas viļņa garums? Parādi aprēķinu gaitu!
Pieraksti dotajā zīmējumā burtu A uz ekrāna novērotajiem punktiem, kas atbilst pirmās kārtas difrakcijas attēlam aprēķinātajam viļņa garumam! Argumentē savu izvēli!
Difrakcijas režģa formula \(d\sin{\varphi}=k\lambda\), kur \(d\) – difrakcijas režģa konstante, \(\varphi\) – difrakcijas leņķis, \(k\) – difrakcijas maksimuma kārtas numurs, \(\lambda\) – starojuma viļņa garums.
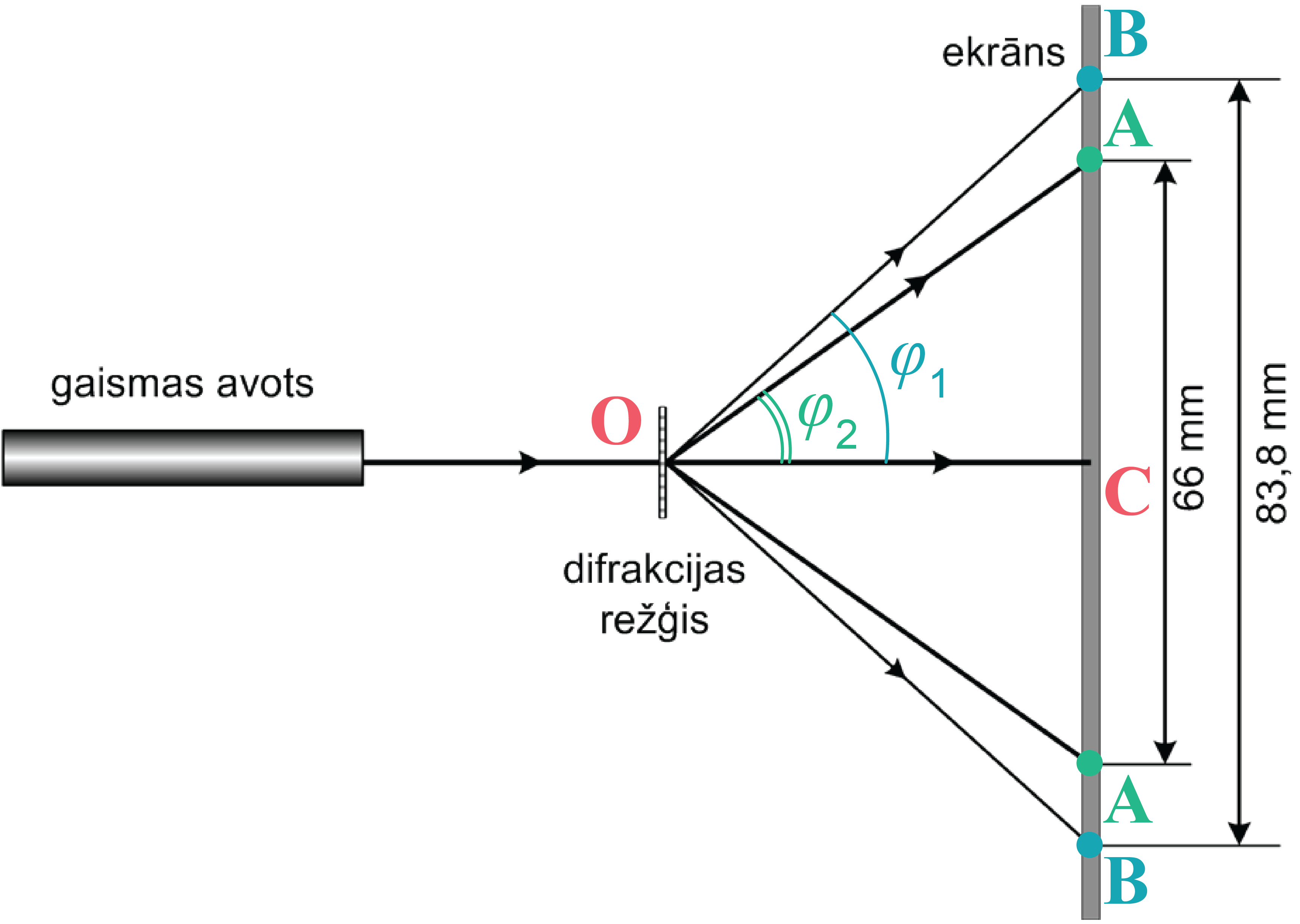
Uzdevumā teikts, ka maksimuma kārtas numurs \(k=1\); pirmā gaismas avota viļņa garums \(\lambda_1=628\space\mathrm{nm}\). Otrā gaismas avota viļņa garums \(\lambda_2<\lambda_1\). Attālums \(\mathrm{OC}=78,5\space\mathrm{mm}\).
Uzdevumā nav zināma difrakcijas režģa konstante \(d\).
No difrakcijas režģa formulas \(d\sin{\varphi}=k\lambda\) secina, ka \(\sin{\varphi}\) ir tieši proporcionāls viļņa garumam \(\lambda\), jo \(d=\mathrm{const}\) un \(k=1\). Uzdevuma tekstā ir teikts, ka \(\lambda_2<\lambda_1\). Tādēļ \(sin{\varphi_2}
Uzdevumu var atrisināt, nezinot difrakcijas režģa konstantes skaitlisko vērtību. Uzraksta katram viļņa garumam difrakcijas režģa formulu, iegūst divu vienādojumu sistēmu \(\begin{cases} d\sin{\varphi_1}=k\lambda_1\\ d\sin{\varphi_2}=k\lambda_2 \end{cases}\), kur \(\varphi_1\) un \(\varphi_2\) atbilstošie difrakcijas leņķi (skatīt attēlu).
Pēc tam pirmo vienādojumu dala ar otro un iegūst \(\frac{sin{\varphi_1}}{sin{\varphi_2}}=\frac{\lambda_1}{\lambda_2}\). No izteiksmes izsaka nezināmo viļņa garumu \(\lambda_2=\frac{\lambda_1\sin{\varphi_2}}{\sin{\varphi_1}}\).
Difrakcijas leņķa sinusu nosaka no taisnleņķa trijstūra:
\(sin{\varphi_1}=\frac{\mathrm{BC}}{\mathrm{OB}}=\frac{\mathrm{BC}}{\sqrt{\mathrm{OC}^2+\mathrm{BC}^2}}\)
\(sin{\varphi_2}=\frac{\mathrm{AC}}{\mathrm{OA}}=\frac{\mathrm{AC}}{\sqrt{\mathrm{OC}^2+\mathrm{AC}^2}}\)
Aprēķini:
\(sin{\varphi_1}=\frac{\mathrm{BC}}{\mathrm{OB}}=\frac{\mathrm{BC}}{\sqrt{\mathrm{OC}^2+\mathrm{BC}^2}}=\frac{41,9}{\sqrt{78,5^2+41,9^2}}\approx0,471\)
\(sin{\varphi_2}=\frac{\mathrm{AC}}{\mathrm{OA}}=\frac{\mathrm{AC}}{\sqrt{\mathrm{OC}^2+\mathrm{AC}^2}}=\frac{33}{\sqrt{78,5^2+33^2}}\approx0,388\)
\(\lambda_2=\frac{\lambda_1\sin{\varphi_2}}{\sin{\varphi_1}}=\frac{628\space\mathrm{nm}\cdot 0,388}{0,471}\approx517\space\mathrm{nm}\)
Piezime: var vispirms no formulas \(d\sin{\varphi_1}=k\lambda_1\) noteikt difrakcijas režģa konstanti \(d=\frac{k\lambda_1}{\sin{\varphi_1}}\). Pēc tam aprēķina otrā gaismas avota viļņa garumu \(\lambda_2=\frac{d\sin{\varphi_2}}{k}\).
Aprēķini:
\(d=\frac{k\lambda_1}{\sin{\varphi_1}}=\frac{1\cdot628\cdot 10^{-9}}{0,471}\approx1,33\cdot 10^{-6}\space\mathrm{m}\)
\(\lambda_2=\frac{d\sin{\varphi_2}}{k}=\frac{1,33\cdot 10^{-6}\cdot 0,388}{1}\approx 516\cdot10^{-9}\space\mathrm{m}=516\space\mathrm{nm}\)
Atbilde: nezināmā gaismas avota viļņa garums ir \(516\space\mathrm{nm}\). Punkts A atrodas tuvāk centrālajam difrakcijas maksimumam (skatīt attelu).
Vērtēšanas kritēriji
Zina vai atrod formulu lapā difrakcijas režģa formulu – 1 punkts.
Nosaka difrakcijas leņķa sinusu no taisnleņķa trijstūra – 1 punkts.
Iegūst izteiksmi nezināmā gaismas viļņa garuma aprēķināšanai – 1 punkts.
Aprēķina nezināmo gaismas viļņa garumu – 1 punkts.
Novērtē punkta A atrašanās vietu uz ekrāna un iezīmē to attēlā simetriski abās vietās – 1 punkts.