Zaļās gaismas stars krīt uz plakanparalēlu taisnstūra stikla plāksnīti, kā parādīts attēlā. Gaismas laušanas koeficients stiklā ir 1,5.
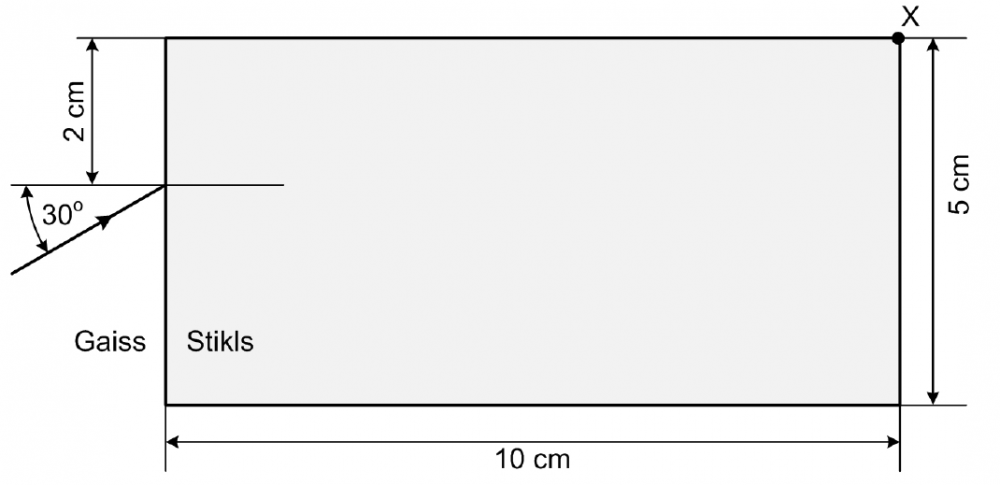
Aprēķini nepieciešamos leņķus un nogriežņus! Precīzi attēlo šajā pašā zīmējumā stara tālāko gaitu, kamēr stars pirmo reizi iznāk no stikla! Norādi zīmējumā aprēķināmos leņķus! Iezīmē punktu A, kurā stars iznāk no stikla! Aprēķini attālumu AX! Cik lielā leņķī \(\Theta\) stars iznāk no stikla? Parādi aprēķinu gaitu!
Punktā \(\mathrm{B}\) zaļās gaismas stars krīt uz plakanparalēlu plāksnīti. Lai noteiktu stara tālāko gaitu, jāizmanto gaismas laušanas likums: \(\frac{\sin\alpha}{\sin\gamma}=\frac{n_2}{n_1}\), kur \(\alpha\) – krišanas leņķis, \(\gamma\) – laušanas leņķis, \(n_1\) – pirmās vides absolūtais gaismas laušanas koeficients (uzdevumā – gaiss), \(n_2\) – otrās vides absolūtais gaismas laušanas koeficients (uzdevumā – stikls). Ir zināms, ka gaisa absolūtais laušanas koeficients ir aptuveni vienāds ar 1. Apzīmē stikla absolūto laušanas koeficientu \(n_2\) ar \(n\). Tad gaismas laušanas likuma formulu pieraksta šādi: \(\frac{\sin\alpha}{\sin\gamma}=n\).
Uzdevuma tekstā stikla laušanas koeficients \(n=1,5\) un punktā \(\mathrm{B}\) krišanas leņķis \(\alpha=30^\mathrm o\). No formulas \(\frac{\sin\alpha}{\sin\gamma}=n\) nosaka laušanas leņķi \(\gamma\):
\(\sin\gamma=\frac{\sin\alpha}{n}=\frac{\sin 30^\mathrm o}{1,5}\approx0,33\space\implies\space\gamma=\mathrm{arcsin(0,33)}\approx19^\mathrm o\).
Attālumu \(\mathrm{YP}\) nosaka no taisnleņķa trijstūra \(\mathrm{BYP}\): \(\mathrm{YP=\frac{YB}{tg\gamma}=\frac{2}{tg19^o}\approx5,8\space cm}\).
Tādēļ nogriežņa \(\mathrm{PX}\) garums ir \(\mathrm{10-5,8=4,2\space cm}\).
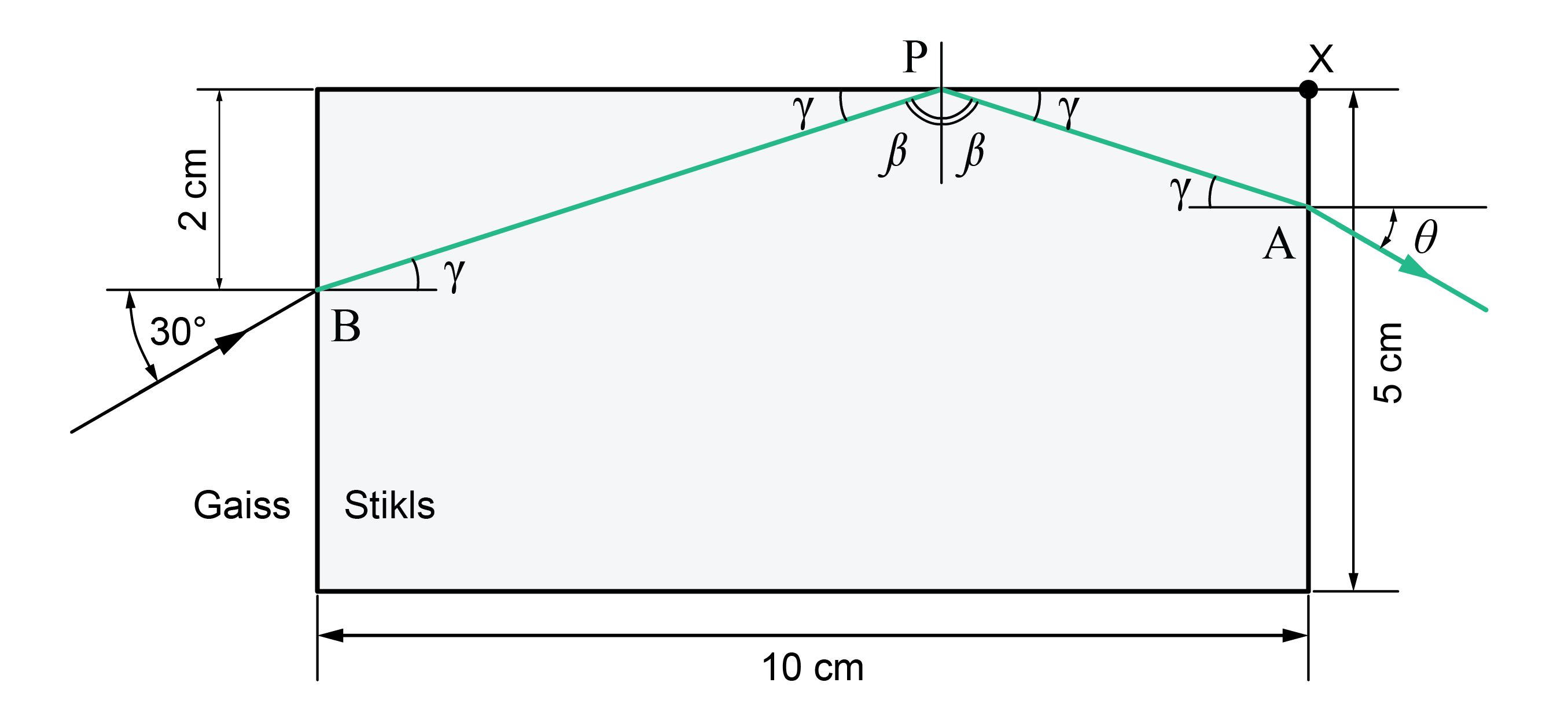
Tālāk noskaidro, kāda parādība notiek punktā \(\mathrm{P}\): laušana vai pilnīgā iekšējā atstarošana.
Pilnīgo iekšējo atstarošanu var novērot, ja gaisma pāriet no vides ar lielāku laušanas koeficientu vidē ar mazāku laušanas koeficientu. Uzdevumā šāda situācija ir iespējama, ja gaismas stars iziet no stikla gaisā. Pilnīgās iekšējās atstarošanas robežleņķi \(\alpha_0\) nosaka no formulas \(\frac{\sin\alpha_0}{\sin\gamma_{\mathrm{max}}}=\frac{n_2}{n_1}\), kur \(n_1=1,5\) – stikla laušanas koeficients, \(n_2=1\) – gaisa laušanas koeficients, \(\gamma_{\mathrm {max}}=90^\mathrm o\) – maksimālais laušanas leņķis. Tad \(\sin\alpha_0=\frac{\sin\gamma_{\mathrm{max}}n_2}{n_1}=\frac{\sin90^\mathrm o\cdot1}{1,5}\approx0,67\space\implies\space\alpha_0=\mathrm{arcsin0,67}\approx42^\mathrm o\).
Punktā \(\mathrm{P}\) krišanas leņķis \(\beta\) un leņķis \(\gamma=19^\mathrm o\) kopā veido \(90^\mathrm o\) lielu leņķi. Tādēļ krišanas leņķis \(\beta=90^\mathrm o-19^\mathrm o=71^\mathrm o\). Secina, kā \(\mathrm{P}\) punktā nenotiek gaismas stara laušana, bet gan notiek pilnīgā iekšējā atstarošana.
Attālumu \(\mathrm{XA}\) nosaka no taisnleņķa trijstūra \(\mathrm{PXA:\space XA=PX\cdot tg\gamma=4,2\cdot tg19^\mathrm o\approx1,4\space cm}\).
Punktā \(\mathrm A\) stara krišanas leņķis \(\gamma\) vienāds ar \(19^\mathrm o\), kas ir mazāks nekā pilnīgās iekšējās atstarošanas robežleņķis \(\alpha_0=42^\mathrm o\). Tādēļ punktā \(\mathrm A\) notiek gaismas stara laušana.
Ģeometriskajā optikā pastāv "stara apgriežamības princips". Tādēļ leņķis \(\Theta\) ir vienāds ar \(30^\mathrm o\).
Var arī leņķi \(\Theta\) noteikt no gaismas laušanas likuma formulas. Tikai tagad pirmā vide ir stikls, otrā – gaiss:
\(\frac{\sin19^\mathrm o}{\sin\Theta}=\frac{1}{1,5}\space\implies\space\sin\Theta=1,5\cdot\sin19^\mathrm o\approx0,49\space\implies\space\Theta=\mathrm{arcsin0,49\approx30^o}\)
Atbilde:
\(\mathrm{AX=1,4\space cm}\). Leņķis \(\Theta=30^\mathrm o\).
Vērtēšanas kritēriji
Aprēķina gaismas laušanas leņķi, staram ieejot plakanparalēlajā plāksnē, uzzīmē stara posmu – 1 punkts.
Nosaka krišanas leņķi uz skaldni XY un attēlo leņķi zīmējumā – 1 punkts.
Noskaidro, vai notiks pilnīgā iekšējā atstarošanās no skaldnes XY – 1 punkts.
Aprēķina krišanas leņķi punktā A un attālumu AX un attēlo krišanas leņķi zīmējumā – 1 punkts.
Aprēķina, kādā leņķī \(\Theta\) stars iznāk no stikla, un attēlo leņķi zīmējumā – 1 punkts.