Gaismas stars krīt uz robežvirsmu ledus–gaiss \(60^{\mathrm o}\) lielā leņķī no ledus puses. Kurš ir iespējamais gaismas stara turpinājums? Pamato savu izvēli! Gaismas laušanas koeficients ledū \(n_{\mathrm l}=1,3\), gaisā \(n_{\mathrm g}=1,0\).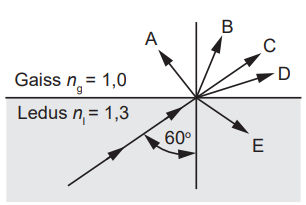
Uzdevuma atrisinājums pieejams video formātā un rakstiski.
Tā kā dotajā uzdevumā gaisma virzās no optiski blīvākas vides uz optiski mazāk blīvu vidi, tad jānoskaidro, vai nenotiek pilnīgā iekšējā atstarošanās. Pilnīgā iekšējā atstarošanās notiek tad, kad gaismas stara krišanas leņķis sasniedz robežvērtību, kuru sauc par pilnīgās iekšējās atstarošanās robežleņķi \(\alpha_0\).
Vispārīgā gadījumā laušanas likuma formula: \(\frac{\sin\alpha}{\sin\gamma}=\frac{n_\mathrm g}{n_\mathrm l}\), kur \(\alpha\) – krišanas leņķis, \(\gamma\) – laušanas leņķis, \(n_\mathrm l\) – pirmās vides absolūtais gaismas laušanas koeficients (uzdevumā – ledus), \(n_\mathrm g\) – otrās vides absolūtais gaismas laušanas koeficients (uzdevumā – gaiss). Robežgadījumā \(\gamma=90^\mathrm o\). Tad \(\sin\alpha_0=\frac{n_\mathrm g}{n_\mathrm l}=\frac{1,0}{1,3}\approx 0,77\). Pilnīgās atstarošanas robežleņķis \(\alpha_0=\arcsin{0,77}\approx50^{\mathrm o}\). Tā kā stars krīt lielākā leņķī nekā pilnīgās iekšējās atstarošanās robežleņķis \(\alpha>\alpha_0\) (\(60^{\mathrm o}>50^{\mathrm o}\)), tad notiek pilnīga iekšējā atstarošanās, un stara turpinājums ir E.
Var formāli no gaismas laušanas likuma noteikt \(\sin\gamma=\frac{\sin\alpha\cdot n_1}{n_2}=\frac{\sin{60^{\mathrm o}}\cdot 1,3}{1}\approx1,1\). Tā kā \(\sin\gamma>1\), tad gaismas laušana nenotiek un stars pilnībā atstarojas – stara turpinājums ir E.
Uzdevuma izpilde eksāmenā - 39,7%.
Vērtēšanas kritēriji
Uzraksta laušanas likuma formulu – 1 punkts.
Aprēķina pilnīgās atstarošanās robežleņķi – 1 punkts.
Secina par stara turpmāko gaitu – 1 punkts.