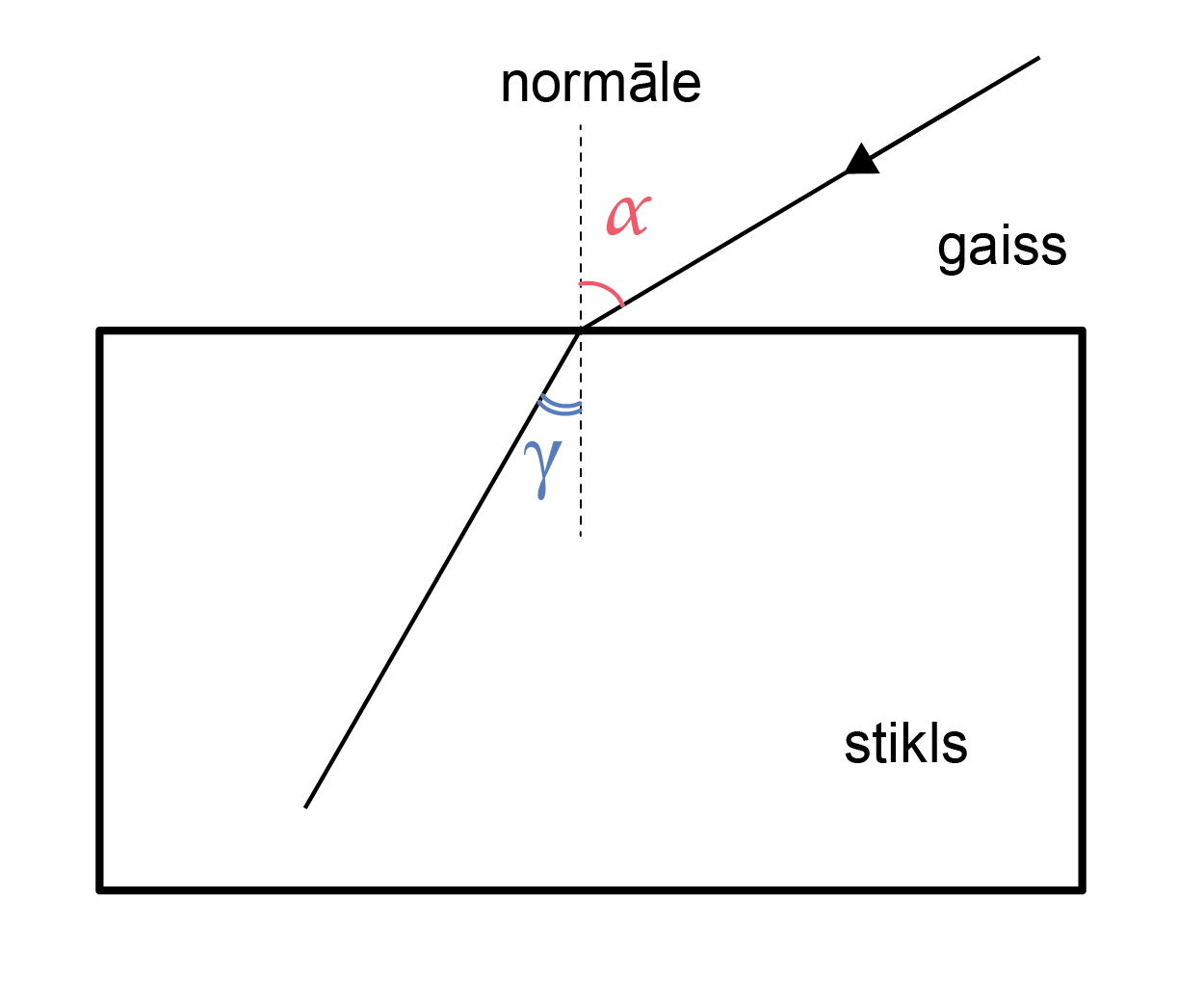
Skolēns laboratorijas darbā pētīja gaismas laušanas likumu, gaismas staram krītot no gaisa uz stikla paralēlskaldni. Skolēns darbā izmantoja sarkanās gaismas lāzeru. Viņš veica sešus krišanas leņķa un laušanas leņķa mērījumus.
Pētāmā problēma: kāda sakarība pastāv starp krišanas leņķa sinusu un laušanas leņķa sinusu?
Uzraksti darba piederumu sarakstu!
Pirmajā mērījumā krišanas leņķis bija \(10^{\mathrm{o}}\). Pēc tam skolēns to palielināja ik pa \(15^{\mathrm{o}}\) un ieguva šādas laušanas leņķa vērtības: \(6,6^{\mathrm{o}}\); \(16^{\mathrm{o}}\); \(25^{\mathrm{o}}\); \(33^{\mathrm{o}}\); \(39^{\mathrm{o}}\); \(42^{\mathrm{o}}\).
Izveido datu tabulu!
Attēlo grafiski \(\sin{\gamma}\) atkarībā no \(\sin{\alpha}\)!
Analizē rezultātus!
Darba piederumu saraksts
sarkanā stara lāzers, stikla paralēlskaldnis, zīmulis, lineāls, transportieris, kniepadatas.
Datu tabula
.png)
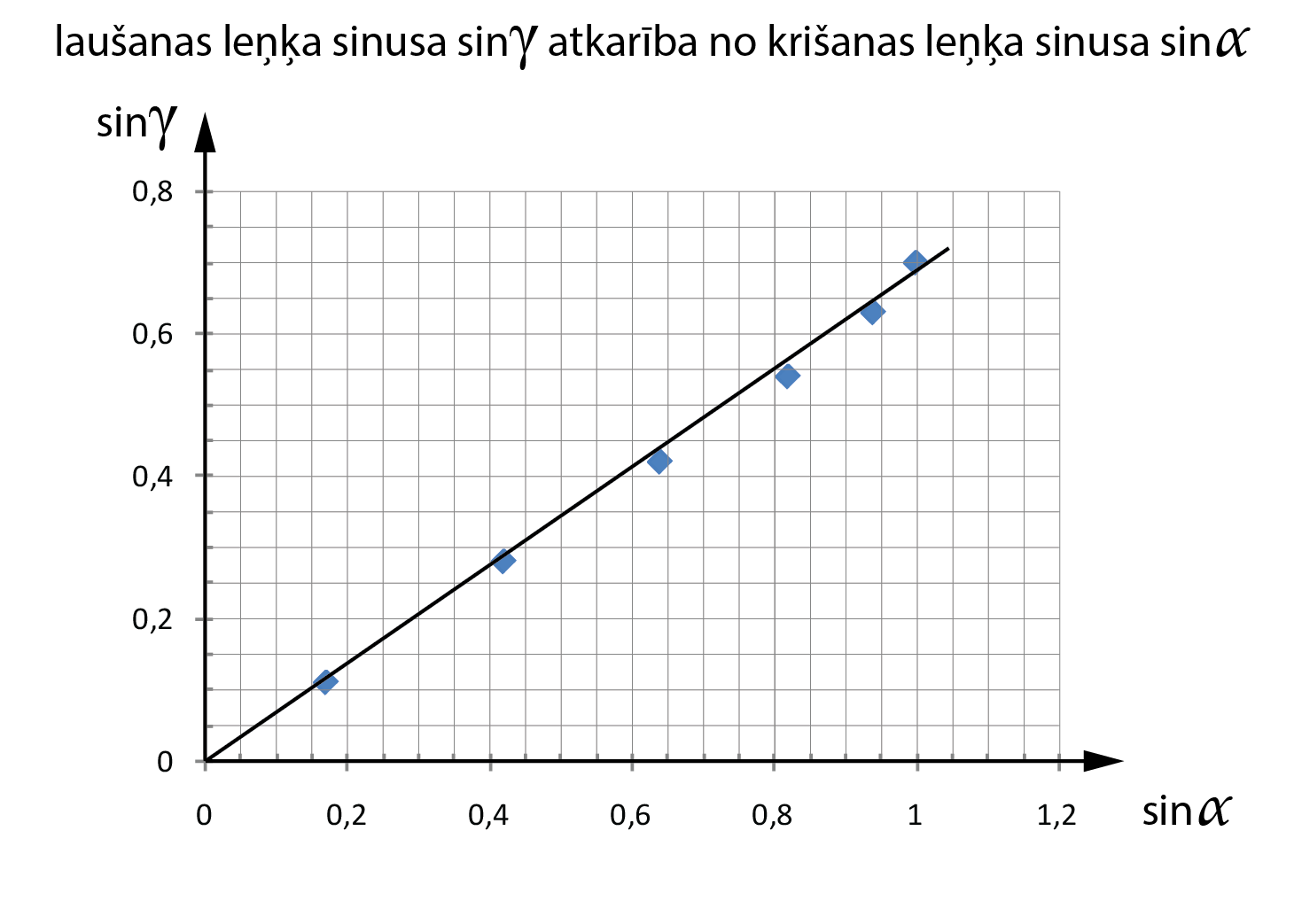
Laušanas leņķa sinusa \(\sin\gamma\) atkarība no krišanas leņķa sinusa \(\sin\alpha\)
Grafikā \(\sin\gamma\) ir atkarīgais lielums – atzīmē pie vertikālās ass, \(\sin\alpha\) ir neatkarīgais lielums – atzīmē pie horizontālās ass. Leņķu sinusus nosaka ar diviem zīmīgajiem cipariem, jo grafikā nav iespējams attēlot sinusa vērtības ar trīs zīmīgajiem cipariem izvēlētā mēroga dēļ.
Rezultātu analīze
1. No tabulas datiem un no grafika ir redzams – ja pieaug \(\sin\alpha\), tad pieaug arī \(\sin\gamma\).
2. Grafikā laušanas leņķa sinusa atkarība no krišanas leņķa sinusa ir taisne, kas šķērso koordinātu sākumpunktu. Tādēļ var secināt, ka \(\sin\gamma\) ir tieši proporcionāls \(\sin\alpha\).
3. Attiecība \(\frac{\sin\alpha}{\sin\gamma}=\mathrm{const}\) vai \(\frac{\sin\alpha}{\sin\gamma}=1,5\).
4. Divi pēdējie mērījumi nav precīzi, t.k. atšķirība starp lielo leņķu sinusiem nav ļoti liela.
Vērtēšanas kritēriji
Izveido laboratorijas darba piederumu sarakstu – 1 punkts.
Izveido datu tabulu – 2 punkti.
Vērtē līmeņos:
izveido tabulu krišanas un laušanas leņķa fiksēšanai, aprēķina krišanas leņķa vērtības, kuras nav dotas, papildina tabulu krišanas un laušanas leņķa sinusa fiksēšanai, aprēķina krišanas un laušanas leņķa sinusa vērtības – 2 punkti;
pieļauj nelielas neprecizitātes, piemēram, neieraksta krišanas leņķa vērtības, kuras nav dotas – 1 punkts;
tabula nav izveidota vai izveidota haotiski, leņķu sinusu vērtības neprecīzas – 0 punkti.
Laušanas leņķa sinusa \(\sin{\gamma}\) atkarības krišanas leņķa sinusa \(\sin{\alpha}\) grafiskā attēlošana - 2 punkti.
Vērtē līmeņos:
izvēlas atbilstošu mērogu, graduē asis vienmērīgi, pieraksta lielumu nosaukumus pie asīm, atliek tabulā dotos punktus grafikā, uzzīmē grafika līniju (taisni), kamēr tā šķērso koordinātu sistēmas sākuma punktu – 2 punkti;
pieļauj vienu kļūdu, piemēram, sajauktas koordinātas asis, asis graduētas nevienmērīgi, nav pareizs mērogs pie ass, grafika līnija nav taisne – 1 punkts;
pieļauj divas vai vairāk kļūdas – 0 punkti.
Izdara secinājumus par laušanas leņķa un krišanas leņķa sinusa sakarību un eksperimenta nepilnībām – 1 punkts.