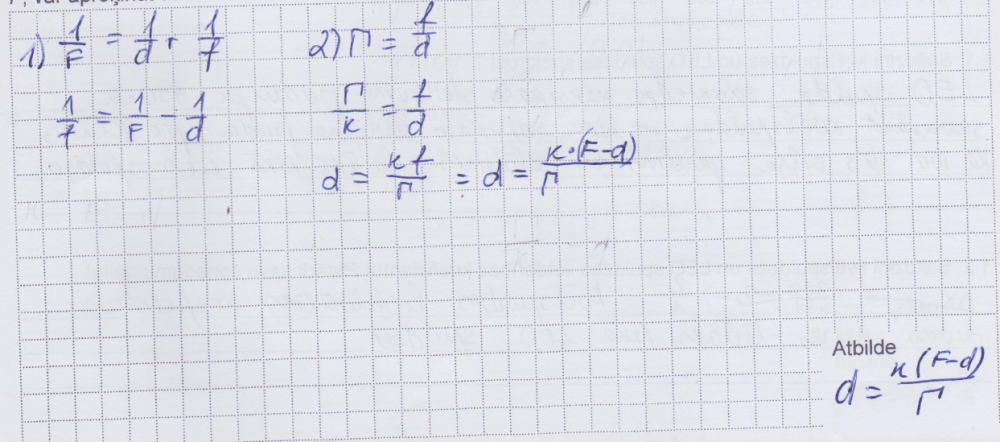Savācējlēcas fokusa attālums ir \(F\). Kādā attālumā \(d\) no lēcas jānovieto priekšmets, lai iegūtu \(k\) reizes samazinātu attēlu?
Izmanto fizikas formulas un parādi, kā, izmantojot tikai uzdevumā dotos lielumus \(k\) un \(F\), var aprēķināt attālumu \(d\)!
Samazināts attēls savācējlēcā var būt tikai reāls. Uzdevumu veic, izmantojot divas formulas: plānas lēcas formulu \(\frac{1}{F}=\frac{1}{d}+\frac{1}{f}\) un lineārā palielinājuma formulu \(\Gamma=\frac{f}{d}\), kur \(F\) – lēcas fokusa attālums, \(\Gamma\) – attēla lineārais palielinājums, \(d\) – attālums no priekšmeta līdz lēcai, \(f\) – attālums no lēcas līdz attēlam.
Uzdevumā ir teikts, kā attēls lēcā ir \(k\) reizes samazināts. Tādēļ \(\Gamma=\frac{1}{k}\).
No izteiksmes \(\frac{1}{k}=\frac{f}{d}\) izsaka lielumu \(f=\frac{d}{k}\) un ievieto lēcas formulā \(\frac{1}{F}=\frac{1}{d}+\frac{1}{f}\).
\(\frac{1}{F}=\frac{1}{d}+\frac{1}{\frac{d}{k}}\space\implies\space\) \(\frac{1}{F}=\frac{1}{d}+\frac{k}{d}\space\implies\space \frac{1}{F}=\frac{1+k}{d}\space\implies\space d=F(k+1)\)
Atbilde: Priekšmeta attālumu līdz lēcai var aprēķināt pēc formulas \( d=F(k+1)\).
Piezīme: Tā kā uzdevumā nekas nav teikts par \(k\) iespējamām vērtībām, tad, iespējams, \(k\) var būt arī mazāks par 1. Tādā gadījumā palielinājuma aprēķināšanai var izmantot izteiksmi \(\Gamma=k\). Tad risinājums būs tāds:
\(k=\frac{f}{d}\space\implies\space f=kd\)
\(\frac{1}{F}=\frac{1}{d}+\frac{1}{f}\space\implies\space \frac{1}{F}=\frac{1}{d}+\frac{1}{kd}\space\implies\space \frac{1}{F}=\frac{k+1}{kd}\space\implies\space d=\frac{F(k+1)}{k}\)
Atbilde: Priekšmeta attālumu līdz lēcai var aprēķināt pēc formulas \(d=\frac{F(k+1)}{k}\).
Vērtēšanas kritēriji
Zina un izmanto lēcas lineārā palielinājuma formulu – 1 punkts.
Zina un izmanto lēcas formulu – 1 punkts.
Apvieno abas formulas un iegūst izteiksmi attāluma d aprēķināšanai vismaz vienā veidā – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
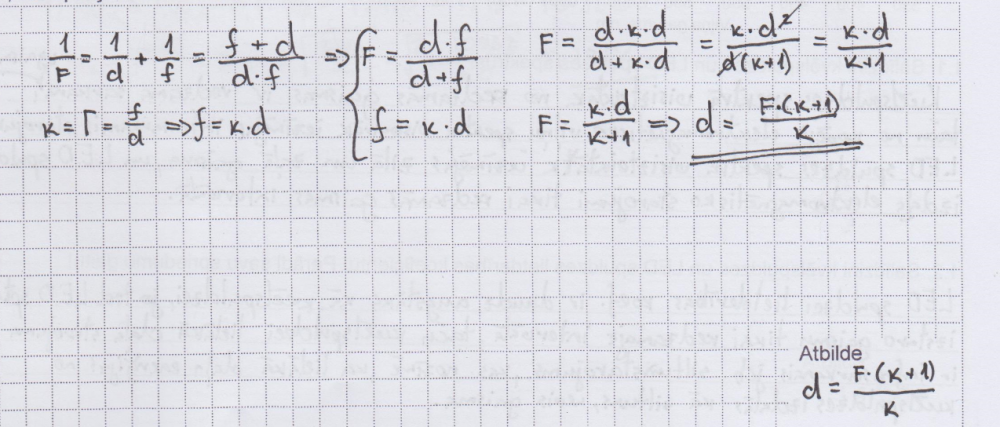
2. piemērs: risinājums novērtēts ar 3 punktiem.
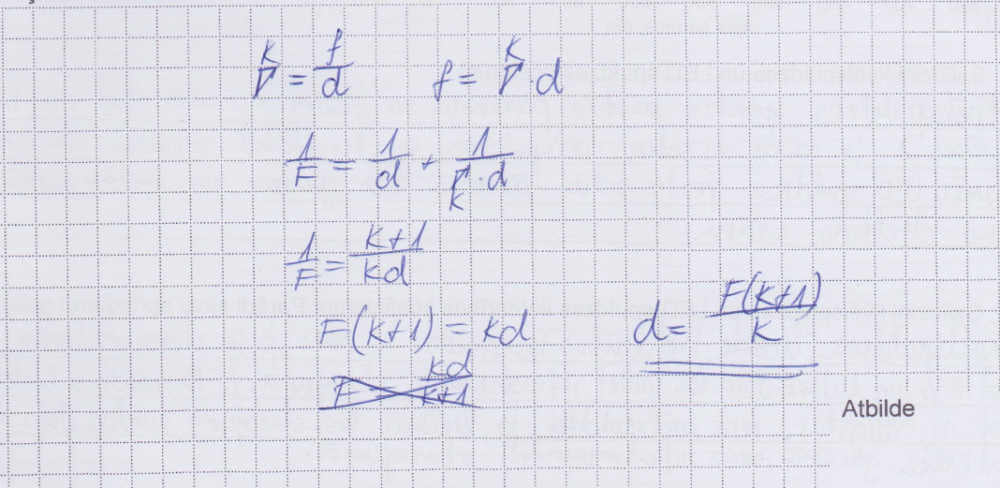
3. piemērs: risinājums novērtēts ar 2 punktiem (gala izteiksmē tiek izmantots attalums f, kas uzdevuma nosacījumos nav dots).

4. piemērs: risinājums novērtēts ar 1 punktu (gala izteiksmē tiek izmantots attalums f, kas uzdevuma nosacījumos nav dots; attalums d ir abās vienādojuma pusēs).