Lēkājošā rotaļlieta sastāv no galvas un atsperes. Rotaļlieta novietota uz galda. Rotaļlietas smaguma centrs atrodas atsperes
stiprinājuma vietā (sk. attēlu). Atsperes pamatnei piestiprināta plāna plāksnīte, kuras biezumu var neievērot. 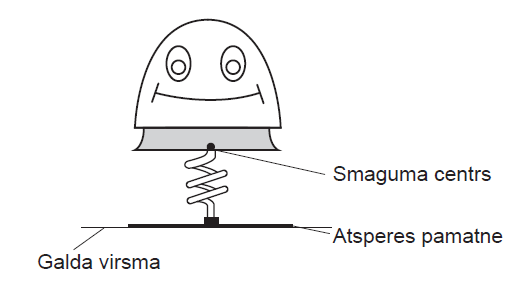
Rotaļlietas kopējā masa ir \(m=\mathrm{80\space g}\), nesaspiestas atsperes garums ir \(l_0=5\space\mathrm{cm}\), un stinguma koeficients \(k=240\space\mathrm{N/m}\).
Turot rotaļlietu aiz galvas, atsperi vispirms piespiež pie galda virsas un pēc tam atlaiž. Saspiestā stāvoklī atsperes garums ir
\(l_1=3\space\mathrm{cm}\). Brīvās krišanas paātrinājums \(g=10\space\mathrm{m/s^2}\).
Aprēķini, cik lielā augstumā \(h\) virs galda paceļas atsperes pamatne brīdī, kad rotaļlieta sasniedz maksimālo augstumu! Parādi aprēķinu gaitu!
1. variants (izmantojot enerģijas nezūdamības likumu)
Pēc atsperes saspiešanas rotaļlietai piemīt elastīgi deformētā ķermeņa potenciālā enerģija \(W_\mathrm{el}=\frac{k(l_0-l_1)^2}{2}\), kur \(k\) – atsperes stinguma koeficients, \(l_0\) – nesaspiestas atsperes garums, \(l_1\) – saspiestās atsperes garums.
Pēc atsperes atlaišanas atsperes potenciālā enerģija pariet smaguma spēka potenciālajā enerģijā \(W_\mathrm{p}=mgh_\mathrm{max}\), kur \(m\) – rotaļlietas masa, \(h_\mathrm{max}\) – rotaļlietas smaguma centra pacelšanas augstums virs sākotnējā stāvokļa.
Lēkšanas laikā rotaļlietas atspere pieņem nedeformēto stāvokli vai pagarināsies par \(l_0-l_1\). Tātad atsperes pamatne paceļas par \(l_0-l_1\) mazāk, nekā rotaļlietas smaguma centrs. Atsperes pamatnes pacelšanas augstums \(h\) virs virsmas: \(h=h_\mathrm{max}-(l_0-l_1)\).
Rotaļlietas smaguma centra pacelšanas augstumu virs sākotnējā stāvokļa nosaka, izmantojot enerģijas nezūdamības likumu: \(W_\mathrm{el}=W_\mathrm{p}\). Ievietojot atbilstošās izteiksmes, iegūst:
\(\frac{k(l_0-l_1)^2}{2}=mgh_\mathrm{max}\) \(\implies\space\space h_\mathrm{max}=\frac{k(l_0-l_1)^2}{2mg}\).
Atsperes pamatnes pacelšanas augstums \(h\) virs virsmas \(h=\frac{k(l_o-l_1)^2}{2mg}-(l_0-l_1)=\frac{240\cdot(0,05-0,03)^2}{2\cdot0,08\cdot10}-(0,05-0,03)=0,04 \space \mathrm{m}\).
2. variants (izmantojot spēkus)
Jāaplūko trīs kustības posmi.
a) Rotaļlieta stāvot uz grīdas, atspere iztaisnojas no maksimālas deformācijas (\(x=l_0-l_1\)) līdz stāvoklim, kad smaguma spēks un elastības spēks būs vienādi. Atsperes deformācija \(s\) tādā gadījumā būs \(s=\frac{mg}{k}\). Uz rotaļlietu darbojas divi spēki – uz augšu vērsts elastības spēks un uz leju vērsts smaguma spēks. Kopspēks (elastības spēka un smaguma spēka vektoru summa) lineāri samazinās: \(F_\mathrm{max}=kx-mg,\space F_\mathrm{min}=0\). Tātad var izmantot kopspēka vidējo aritmētisko vērtību \(F_\mathrm{vid}=\frac{kx-mg}{2}\). Atsperes iztaisnošanas laikā rotaļlietas vidējais paātrinājums \(a_\mathrm{vid}=\frac{kx-mg}{2m}\).
Kad atspere ir iztaisnota par \(l=x-s\), rotaļlietas ātrumu nosaka pēc formulas \(l=\frac{v^2-v_0^2}{2a}\), kur \(l=x-s\), \(a=a_\mathrm{vid}=\frac{kx-mg}{2m}\), \(v_0=0\). Iegūst \(v^2=(x-s)\frac{kx-mg}{m}\).
b) Rotaļlieta stāv uz grīdas, atspere iztaisnojas no deformācijas \(s=\frac{mg}{k}\) līdz nedeformētajam stāvoklim. Uz rotaļlietu darbojas uz leju vērsts smaguma spēks un uz augšu vērsts elastības spēks. Elastības spēks pēc moduļa ir mazāks, nekā smaguma spēks. Notiek rotaļlietas bremzēšana, jo kopspēks, kas darbojas uz rotaļlietu, ir vērsts uz leju. Kopspēks (elastības spēka un smaguma spēka vektoru summa) lineāri samazinās: \(\space F_\mathrm{min}=0, F_\mathrm{max}=mg\). Tātad var izmantot kopspēka vidējo aritmētisko vērtību \(F_\mathrm{vid}=\frac{0+mg}{2}\). Atsperes iztaisnošanas laikā rotaļlietas vidējais paātrinājums \(a_\mathrm{vid}=\frac{g}{2}\).
Kad atspere ir iztaisnota vēl \(s\) attālumā, rotaļlietas ātrumu nosaka arī pēc formulas \(l=\frac{v^2-v_0^2}{2a}\), kur \(l=s\), \(a=a_\mathrm{vid}=\frac{g}{2}\), \(v_0^2=(x-s)\frac{kx-mg}{m}\). Iegūst, ka \(v^2=(x-s)\frac{kx-mg}{m}-gs\).
c) Tālāk rotaļlieta atraujas no grīdās, atspere pilnīgi iztaisnota. Izmanto arī formulu \(l=\frac{v^2-v_0^2}{2a}\), tikai pārveidojot to maksimālā augstuma noteikšanai gravitācijas lauka: \(h_\mathrm{vid}=\frac{v_0^2}{2g}\).
Izmantojot iepriekšējā punktā iegūto izteiksmi beigu ātrumam (kas ir sākuma ātruma šajā posmā): \(h_\mathrm{vid}=\frac{(x-s)\frac{kx-mg}{m}-gs}{2g}\).
Ievērojot, ka \(s=\frac{mg}{k}\), iegūst: \(h_\mathrm{vid}=\frac{(x-\frac{mg}{k})\frac{kx-mg}{m}-g\frac{mg}{k}}{2g}=\frac{\frac{kx^2}{m}-\frac{mgkx}{km}-xg+\frac{mg^2}{k}-\frac{mg^2}{k}}{2g}=\frac{\frac{kx^2}{m}-2xg}{2g}=\frac{kx^2}{2gm}-x=\frac{k(l_0-l_1)^2}{2mg}-(l_0-l_1)\).
Aprēķini: \(h=\frac{k(l_o-l_1)^2}{2mg}-(l_0-l_1)=\frac{240\cdot(0,05-0,03)^2}{2\cdot0,08\cdot10}-(0,05-0,03)=0,04 \space \mathrm{m}\).
Atbilde: rotaļlietas pamatnes pacelšanas augstums virs galda virsmas ir \(0,04\space\mathrm{m}\) jeb \(4\space\mathrm{cm}\).
Uzdevuma izpilde eksāmenā – 22%.
Vērtēšanas kritēriji
1. variants
Aprēķina deformētas atsperes enerģiju – 1 punkts.
Aprēķina virs zemes pacelta ķermeņa potenciālo enerģiju – 1 punkts.
Izmanto enerģijas nezūdamības likumu –1 punkts.
Zina, kā pamatnes virsmai pacelšanas augstums ir mazāks, nekā smaguma centra pacelšanas augstums – 1 punkts.
Izsaka augstumu \(h\), ievieto skaitļus, iegūst rezultātu ar mērvienībām – 1 punkts.
2. variants
Zina, kā rotaļlietas kustība sastāv no trim posmiem – 1 punkts.
Aprēķina vidējos paātrinājumus, kad rotaļlieta atrodas uz galda – 1 punkts.
Aprēķina rotaļlietas atraušanas ātrumu no galda – 1 punkts.
Izmanto maksimālās pacelšanas augstuma formulu –1 punkts.
Izsaka augstumu \(h\), ievieto skaitļus, iegūst rezultātu ar mērvienībām – 1 punkts.