Spēlējot skvošu, sportists sit bumbiņu ar raketi pret skvoša korta sienām un grīdu. Viņš novēro, ka spēles sākumā, bumbiņai atsitoties pret sienu vai grīdu, tā ievērojami zaudē ātrumu. Spēlējot skvošu ilgāku laiku, bumbiņa ātrumu zaudē mazāk.
Mēģinot izskaidrot šo parādību, sportists veic eksperimentu. Vispirms viņš izplāno eksperimenta soļus:
1. Pie sienas vertikāli novieto mērlenti, kuras iedaļas vērtība ir \(1\space\mathrm{cm}\).
2. Katlā ar ūdeni iegremdē skvoša bumbiņu un gaida, kamēr temperatūras sensors uzrāda ūdens
temperatūru \(t=60\space ^{\mathrm o}\mathrm C\).
3. Bumbiņu izņem no katla un ļauj tai brīvi krist no \(1,00\space\mathrm{m}\) liela augstuma.
4. Ar videokameras palīdzību fiksē bumbiņas maksimālo pacelšanās augstumu \(h\) pēc sadursmes ar grīdu.
5. Atkārto 2. – 4. soli, katru reizi samazinot temperatūru par \(5\space ^{\mathrm o}\mathrm C\).
Jautājumi un uzdevumi:
1. Kurš pētījumā ir neatkarīgais lielums, un kurš – atkarīgais?
Eksperimentā iegūtie dati apkopoti tabulā:
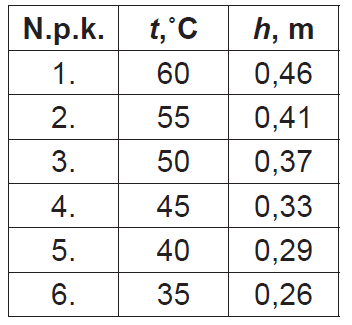
2. Attēlo rezultātus grafiski!
3. Salīdzini pirmā un pēdējā augstuma mērījuma relatīvo kļūdu un pamato savu atbildi!
4. Pēc atlēkšanas no grīdas bumbiņa nesasniedz palaišanas augstumu. Kur paliek enerģijas starpība?
5. Cik liels siltuma daudzums izdalās, skvoša bumbiņai katru reizi atsitoties pret grīdu? Aizpildi tabulu! Skvoša bumbiņas masa ir \(24\space\mathrm{g}\). 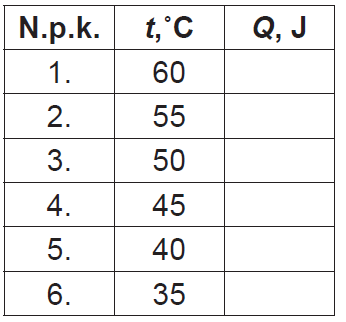
6. Kāpēc, palielinoties temperatūrai, skvoša bumbiņa mazāk zaudē ātrumu? Izmanto tabulas datus!
1. Sportists pēta, kā bumbiņas maksimālais pacelšanās augstums pēc sadursmes ar grīdu ir atkarīgs no bumbiņas temperatūras, ja sākuma krišanas augstums ir nemainīgs.
Neatkarīgais lielums ir tas lielums, kuru sportists mainīja katrā mēģinājumā – bumbiņas temperatūra.
Atkarīgais lielums ir bumbiņas maksimālais pacelšanas augstums pēc sadursmes ar grīdu.
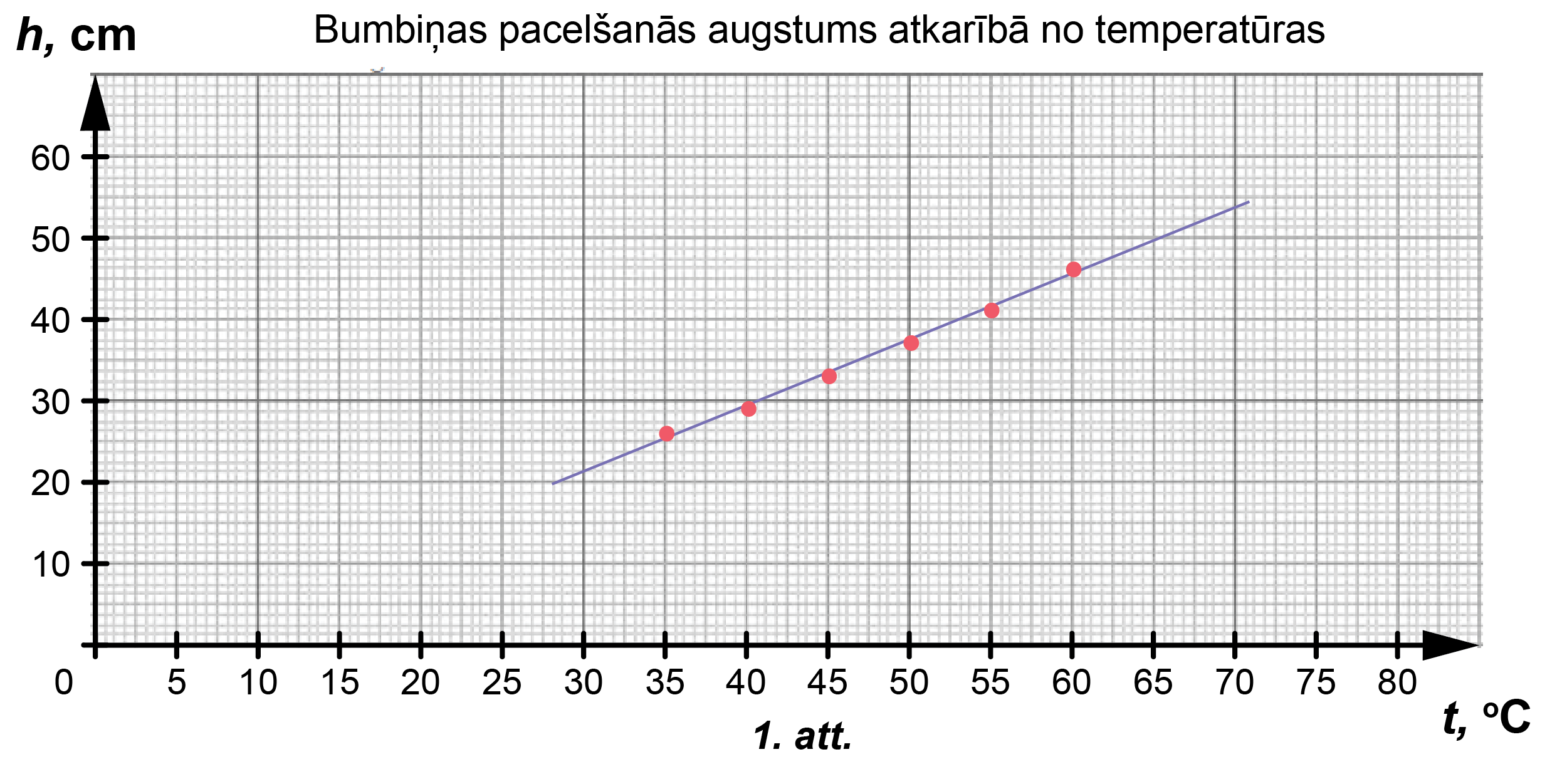
2. Attēlojot grafiski eksperimentā iegūtos rezultātus, uz horizontālās ass vienmēr atliek neatkarīgo lielumu, bet uz vertikālās ass -atkarīgo lielumu. Uzdevumā neatkarīgais lielums ir bumbiņas temperatūra \(t\), bet atkarīgais lielums – bumbiņas maksimālais pacelšanās augstums \(h\) pēc sadursmes ar grīdu. Pie asīm pieraksta fizikālo lielumu apzīmējumus (var tos pierakstīt ar vārdiem) un atbilstošās mērvienības. Izvēlas atbilstošu grafika mērogu. Asis graduē vienmērīgi. Grafika nosaukumam ir jābūt saprotamam. Grafikā atspoguļotajiem datiem jāatbilst veiktajiem mērījumiem. Līkni velk pēc iespējas tuvāk eksperimentālajiem punktiem, līknei jābūt gludai, bez lūzumiem, ja tiem nav papildu eksperimentālo pierādījumu (skatīt 1. attēlu)
3. Mērījuma relatīvo kļūdu \(r\) nosaka pēc formulas \(r=\frac{\Delta h}{h}\cdot 100\%\), kur \(\Delta h\) – mērījuma absolūtā kļūda (uzdevumā \(\Delta h=1\space\mathrm{cm}\)), \(h\) – atbilstošā mērījuma rezultāts.
Aprēķini:
pirmais mērījums. \(r_1=\frac{\Delta h}{h_1}\cdot 100\%=\frac{1}{46}\cdot 100\%\approx2,2\%\);
pēdējais mērījums. \(r_6=\frac{\Delta h}{h_6}\cdot 100\%=\frac{1}{26}\cdot 100\%\approx3,8\%\).
Ir redzams, ka \(r_1>r_6\), jo pēdējā mērījuma rezultāts ir mazāks nekā pirmā mērījuma rezultāts.
4. Bumbiņa pēc atlēkšanas no grīdas nesasniedz palaišanas augstumu, jo ir radušies mehāniskās enerģijas zudumi – daļa bumbiņas mehāniskās enerģijas ir pārgājusi siltumā, skaņā vai bumbiņas materiāla struktūras izmaiņā. Reālā situācijā vienmēr rodas mehāniskās enerģijas zudumi, jo daļa no enerģijas izdalās siltuma veidā berzes un pretestības spēku ietekmē.
5. Pieņem, ka bumbiņas potenciālās enerģijas zudumi saistīti tikai ar siltumu. Tad, saskaņā ar enerģijas nezūdamības likumu: \(W_{\mathrm{pot}0}=W_{\mathrm{pot\space i}}+Q_\mathrm i\) – bumbiņas potenciālā enerģija \(h_0=1\space\mathrm m\) augsumā, \(W_{\mathrm{pot\space i}}=mgh_\mathrm i\) – bumbiņas potenciālā enerģija \(h_\mathrm i\) augstumā (\(\mathrm i\) mainās no 1 līdz 6), \(Q_\mathrm i\)– izdalītais siltuma daudzuma i–tajā mēģinājumā.
No formulas iegūst \(Q_\mathrm i=W_{\mathrm{pot\space i}}-W_{\mathrm{pot\space 0}}=mgh_0-mgh_\mathrm i=mg(h_0-h_\mathrm i)\).
Aprēķina piemērs:
\(Q_\mathrm i=mg(h_0-h_\mathrm i)=0,024\cdot10(1,00-0,46)\approx0,13\space\mathrm J\).
Aizpildīta tabula parādīta 2. attēlā:
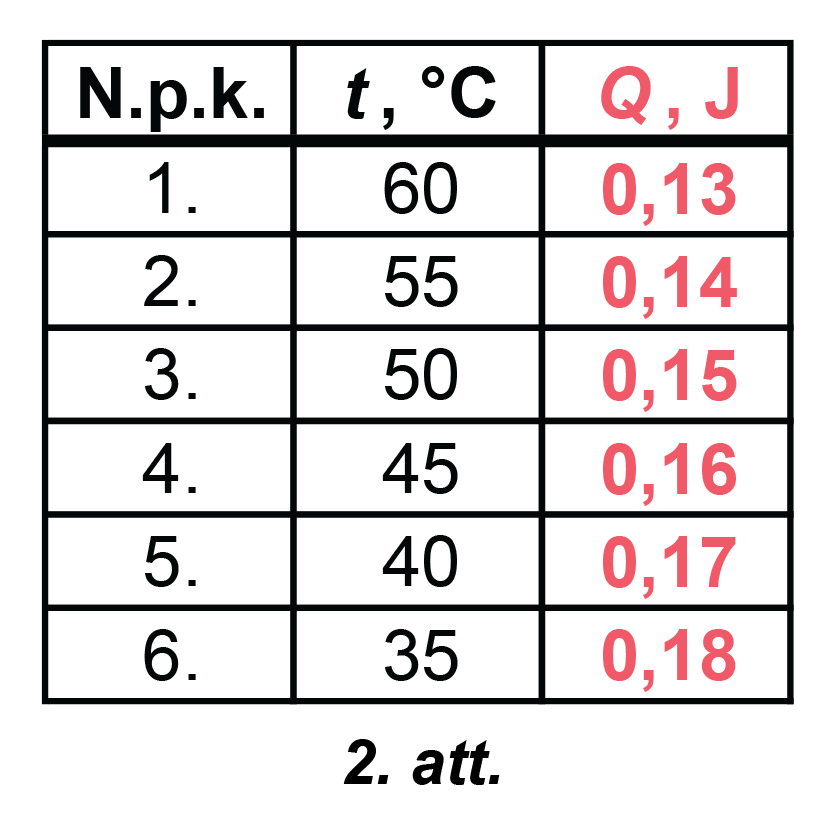
6. Ja bumbiņas temperatūra pieaug, tad enerģijas zudumi samazinās (skatīt 2. attēlu). Iemesls var būt saistīts ar bumbiņas materiāla struktūras izmaiņu. Jo lielāka bumbiņas temperatūra, jo elastīgāka kļūst bumbiņa.
Vērtēšanas kritēriji
1. Vērtē līmeņos
Secina, kurš ir atkarīgais un kurš neatkarīgais lielums – 2 punkti.
Nosaka tikai vienu lielumu – 1 punkts.
2. Vērtē līmeņos
Asīm piešķirti atbilstoši nosaukumi, pie asīm ir mērvienības, asis graduētas vienmērīgi, grafikam ir nosaukums, grafiks aizņem vismaz pusi no tam atvēlētā laukuma – 2 punkti.
Pieļautas ne vairāk kā divas kļūdas – 1 punkts.
Pieļautas trīs vai vairāk kļūdas – 0 punkti.
3. Aprēķina relatīvo kļūdu un salīdzina kļūdas lielumu divos mērījumos – 1 punkts.
4. Analizē mehāniskās enerģijas zudumu rašanās cēloni – 1 punkts.
5. Vērtē līmeņos
Saskaņo mērvienības, aprēķina siltuma daudzumu, noapaļo rezultātu līdz diviem zīmīgajiem cipariem, rezultātu pieraksta ar atbilstošo mērvienību – 2 punkti.
Pieļauj ne vairāk kā divas kļūdas – 1 punkts.
Pieļauj trīs vai vairāk kļūdas – 0 punkti.
6. Analizē iegūtos rezultātus – 1 punkts.