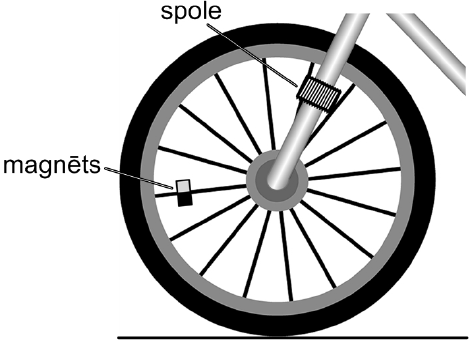
Skolēns savam velosipēdam izveidoja pašgatavotu spidometru. Viņš pie priekšējā riteņa spieķa piestiprināja magnētu, bet pie rāmja – nelielu indukcijas spoli. Spolei pievienoja strāvas stipruma sensoru, kas bija savienots ar datu uzkrājēju.
Grafikā parādīta strāvas stipruma maiņa brīdī, kad velosipēds pārvietojas pa taisnu ceļu bez slīdēšanas.
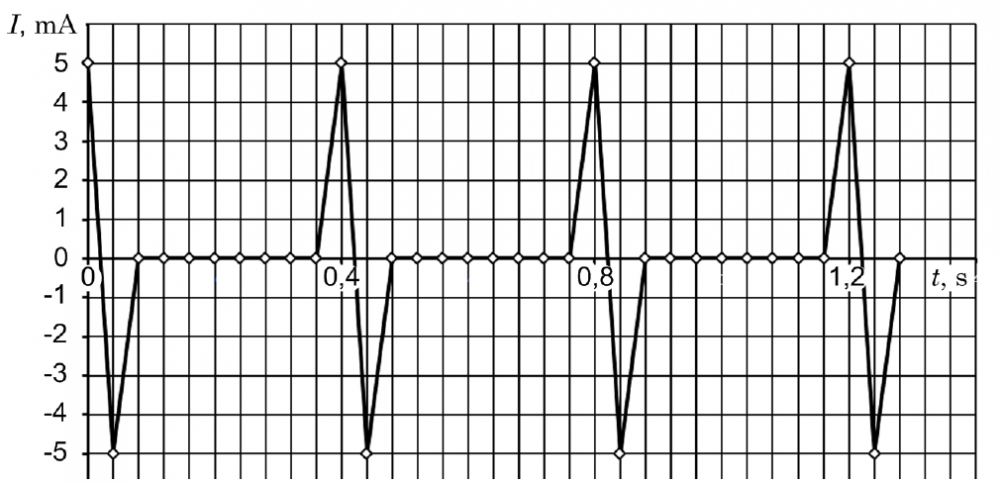
1. Raksturo velosipēda kustību (vienmērīgi paātrināta, vienmērīga, vienmērīgi palēnināta)! Pamato savu atbildi!
2. Izmantojot grafiku, nosaki riteņa rotācijas periodu!
3. Aprēķini riteņa rotācijas frekvenci!
4. Kāds lielums vēl jāizmēra, lai varētu aprēķināt velosipēda kustības ātrumu? Uzraksti formulu, pēc kuras var aprēķināt velosipēda kustības ātrumu!
5. Kā sauc fizikālo parādību, kuras dēļ spolē rodas strāvas impulsi?
6. Kāpēc, palielinoties velosipēda braukšanas ātrumam, maksimālais strāvas stiprums spolē palielinās?
1. Strāvas stipruma maiņas grafika (skatīt attēlu) virsotnes jeb strāvas stipruma maksimālās pozitīvās vērtības (\(I=5\space\mathrm{mA}\)), kas apzīmētas ar punktiem A, B, C un D, atkārtojas pēc vienādiem laika intervāliem. Tādēļ var secināt, ka ritenis griežas ar nemainīgu lineāro ātrumu jeb kā velosipēdista kustība ir vienmērīga.
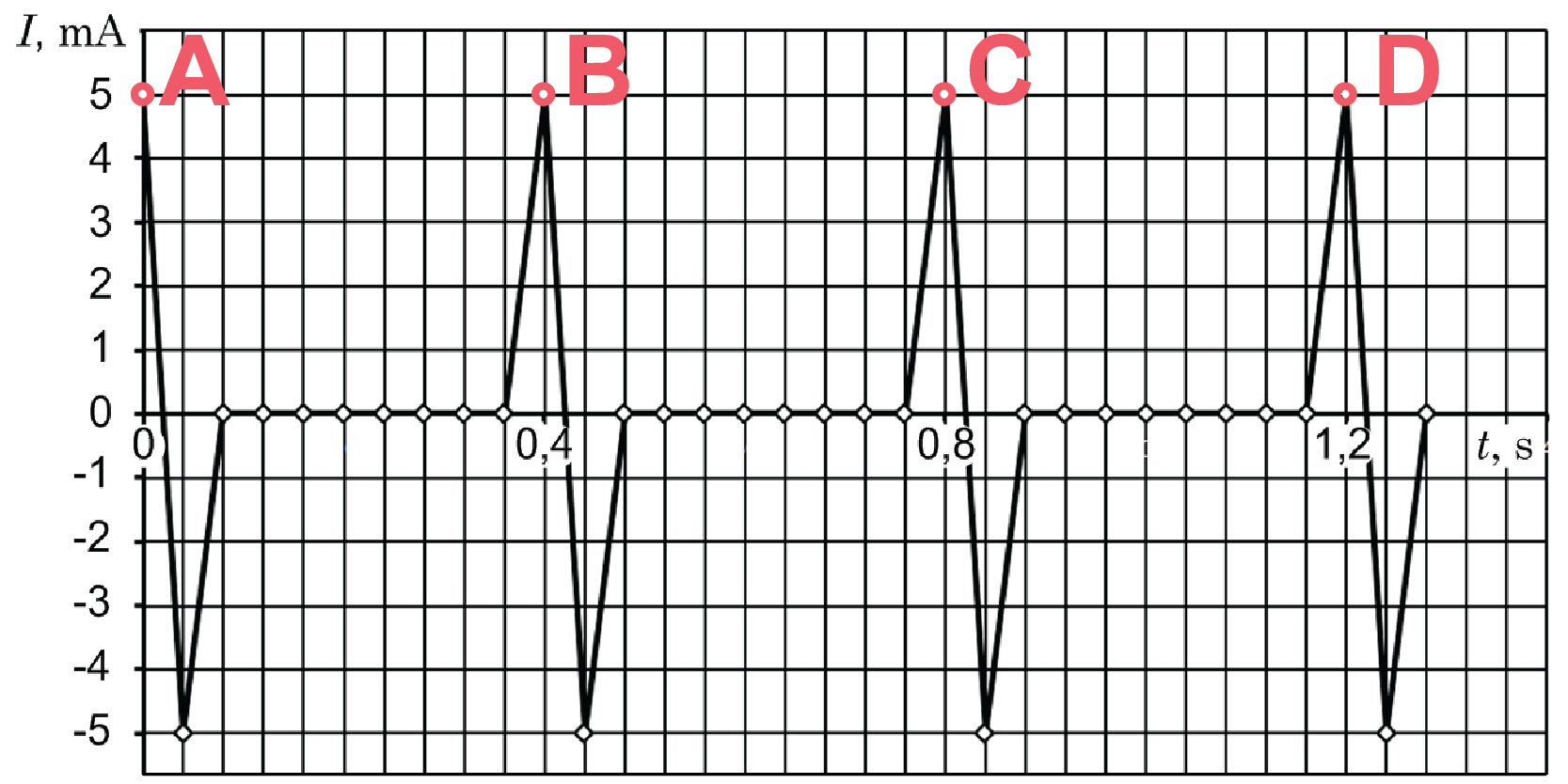
2. Riteņa rotācijas periods \(T\) ir viena apgrieziena laiks. Uzdevumā periods ir laika intervāls starp tuvākajiem laika momentiem, kuros magnēts kustas gar spoli. Pēc grafika (skatīt attēlu 1.) nolasa, ka šāds laika intervāls ir \(0,4\space\mathrm s\).
Atbilde: riteņa rotācijas periods ir \(0,4\space\mathrm s\).
3. Rotācijas frekvenci \(f\) vai apgriezienu skaitu vienā sekundē nosaka pēc formulas \(f=\frac{1}{T}\), kur \(T\) – rotācijas periods.
Aprēķini: \(f=\frac{1}{T}=\frac{1}{0,4\space\mathrm s}=2,5\space\mathrm Hz\).
Atbilde: riteņa rotācijas frekvence ir\(2,5\space\mathrm Hz\).
Piezīme: frekvence var būt arī pierakstīta arī ar mērvienību \(\mathrm {1/s}\) vai \(\mathrm {s^{-1}}\).
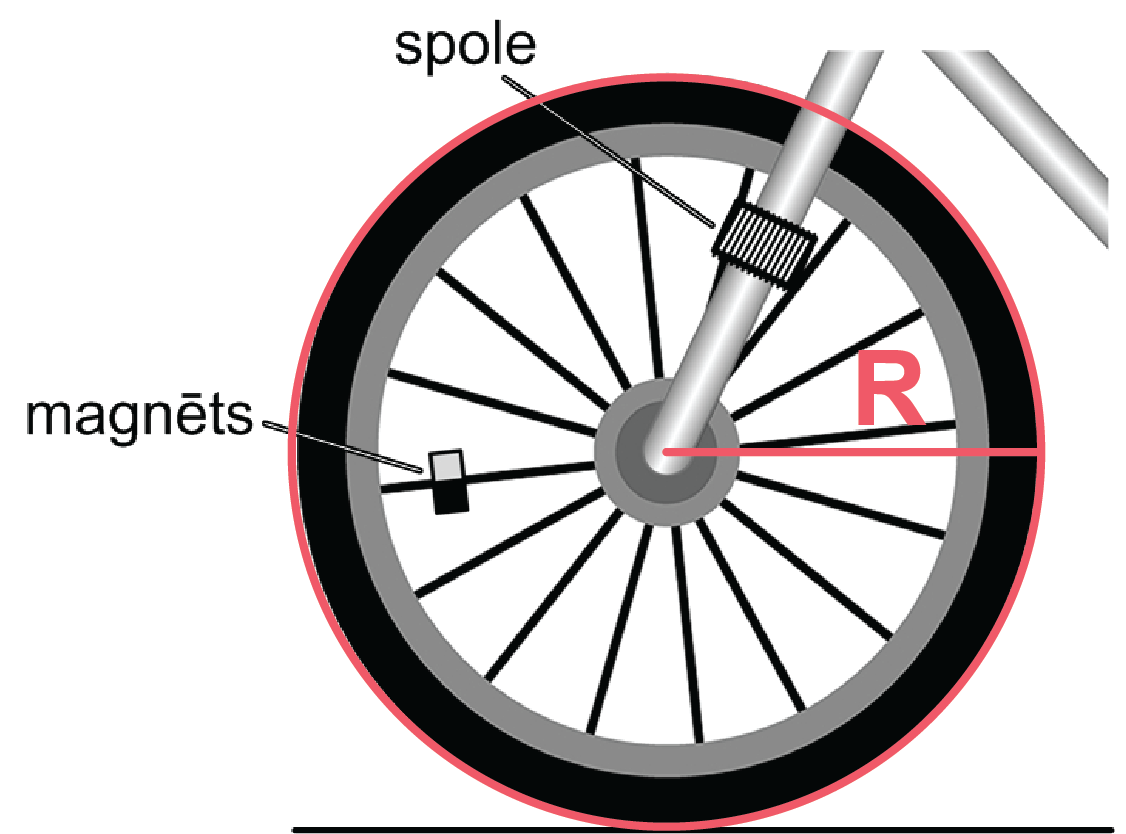
4. Velosipēda kustības ātrums \(v\) ir vienāds ar riteņa malējo punktu rotācijas lineāro ātrumu \(v\) attiecībā pret riteņa centru, jo velosipēda riteņi kustas bez slīdēšanas. Izņemot riteņa centru, visi riteņa punkti griežas ar vienādu periodu \(T\) vai vienādu frekvenci \(f\). Riteņa malējo punktu rotācijas lineāro ātrumu nosaka pēc formulas \(v=\frac{2\pi R}{T}\) vai \(v=2 \pi Rf\).
Tādēļ, lai varētu aprēķināt velosipēda kustības ātrumu, jāizmēra riteņa rādiuss \(R\).
5. Velosipēda kustības laikā spoles vijumos mainās magnētiskā plūsma \(\Phi\) un spolē inducējas elektrodzinējspēks \(\varepsilon_\mathrm i\). Ja spoli noslēdz ar rezistoru vai sensoru (šajā gadījumā), tad ķēdē plūst elektriskā strāva. Parādības nosaukums – elektromagnētiskā indukcija.
6. Indukcijas EDS \(\varepsilon_\mathrm i\) un inducētās strāvas stiprums sensorā ir tieši proporcionāli magnētiskās plūsmas izmaiņas ātrumam spolē \(\varepsilon_\mathrm i=\frac{\Delta\Phi}{\Delta t}\). Tādēļ, palielinoties velosipēda braukšanas ātrumam, palielinās indukcijas EDS \(\varepsilon_\mathrm i\) un maksimālā inducētās strāvas stipruma \(I_\mathrm{max}\) vērtības.
Vērtēšanas kritēriji
1. Vērtē līmeņos
- raksturo velosipēda kustību un pamato savu atbildi – 2 punkti;
- raksturo velosipēda kustību, bet pamatojums ir kļūdains – 1 punkts;
- nav atbildes vai tā ir kļūdaina – 0 punkti.
2. No grafika nosaka riteņa rotācijas periodu un pieraksta to kopā ar mērvienību – 1 punkts.
3. Aprēķina riteņa rotācijas frekvenci un pieraksta to kopā ar mērvienību – 1 punkts.
4. Uzraksta formulu, pēc kuras var aprēķināt velosipēda kustības ātrumu – 1 punkts.
Secina, kāds fizikālais lielums vēl jāizmēra velosipēda kustības ātruma aprēķīnāšanai – 1 punkts.
5. Zina parādības, kuras dēļ spolē rodas strāvas impulsi, nosaukumu – 1 punkts.
6. Skaidro, kāpēc, palielinoties velosipēda braukšanas ātrumam, maksimālais strāvas stiprums spolē palielinās – 1 punkts.