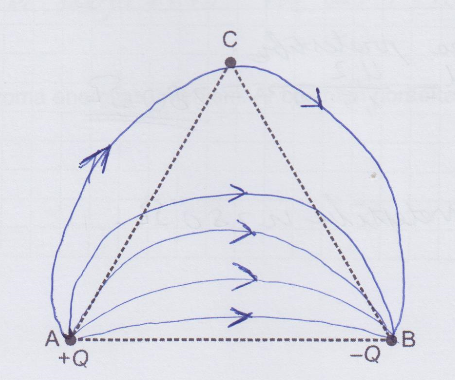
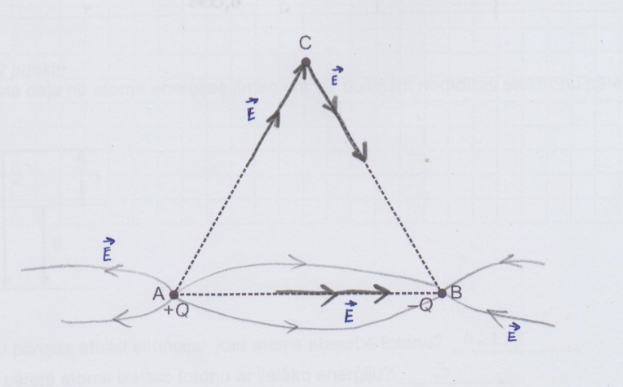
Elektrisko lauku veido punktveida lādiņi \(+Q\) un \(-Q\), kuru moduļi ir vienādi. Attēlo elektriskā lauka intensitātes vektorus \(\overrightarrow{E}\) punktā C, ko veido katrs lādiņš, un rezultējošo elektriskā lauka intensitāti! AC = BC.
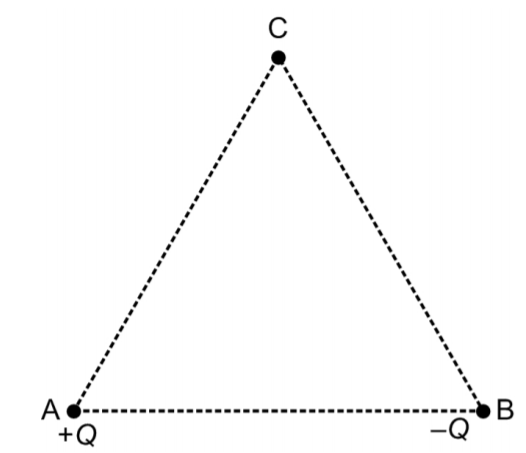
Ap lādētu ķermeni pastāv elektriskais lauks, ko raksturo elektriskā lauka intensitātes vektors \(\overrightarrow{E}\). Ja elektrisko lauku veido punktveida lādiņš, tad elektriskā lauka intensitātes vektors dotajā punktā ir vērsts pa taisni, kas savieno punktveida lādiņu un doto punktu.
Elektriskā lauka intensitāte ir vienāda ar spēku, kas darbojas uz elektriskajā laukā ievietotu pozitīvu vienu vienību lielu punktveida lādiņu. Ja punktveida lādiņš ir pozitīvs, tad lauka intensitātes vektors vērsts prom no lādiņa. Ja punktveida lādiņš ir negatīvs, tad lauka intensitātes vektors vērsts lādiņa virzienā.
Lādiņa \(Q\) lauka intensitātes vektora moduli nosaka pēc formulas \(E=\frac{k\mid Q\mid}{R^2}\), kur \(k\) – Kulona likuma konstante, \(R\) – attālums starp lādiņu un telpas punktu.
Uzdevuma tekstā attālumi starp lādiņiem \(+Q\) un\(-Q\) līdz punktam C ir vienādi AC = BC. Arī lādiņu moduļi ir vienādi. Tādēļ punktā C elektriskā lauka intensitātes vektori no katra lādiņa ir vienādi pēc moduļa.
No sākuma konstruē vektoru \(\overrightarrow{E}_{\mathrm{A}}\) virzienā prom no lādiņa punktā A. Tālāk konstruē vektoru \(\overrightarrow{E}_{\mathrm{B}}\) virzienā uz lādiņu B. Lai iegūtu rezultējošo intensitātes vektoru, konstruē paralelogramu, kuru malas ir vektori \(\overrightarrow{E}_{\mathrm{A}}\) un \(\overrightarrow{E}_{\mathrm{B}}\) . Paralelograma diagonāle ir vektoru \(\overrightarrow{E}_{\mathrm{A}}\) un \(\overrightarrow{E}_{\mathrm{B}}\) summa jeb rezultējošais elektriskā lauka intensitātes vektors \(\overrightarrow{E}\)punktā C (sk. att.)

Vērtēšanas kritēriji
Pamato, kāpēc intensitātes vektoru moduļi ir vienādi. Attēlo intensitātes vektorus, ievērojot to garumus – 1 punkts.
Attēlo intensitātes vektorus, ievērojot to virzienu – 1 punkts.
Konstruē paralelogramu un attēlo rezultējošo intensitātes vektoru, pieraksta pie vektoriem to apzīmējumus – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
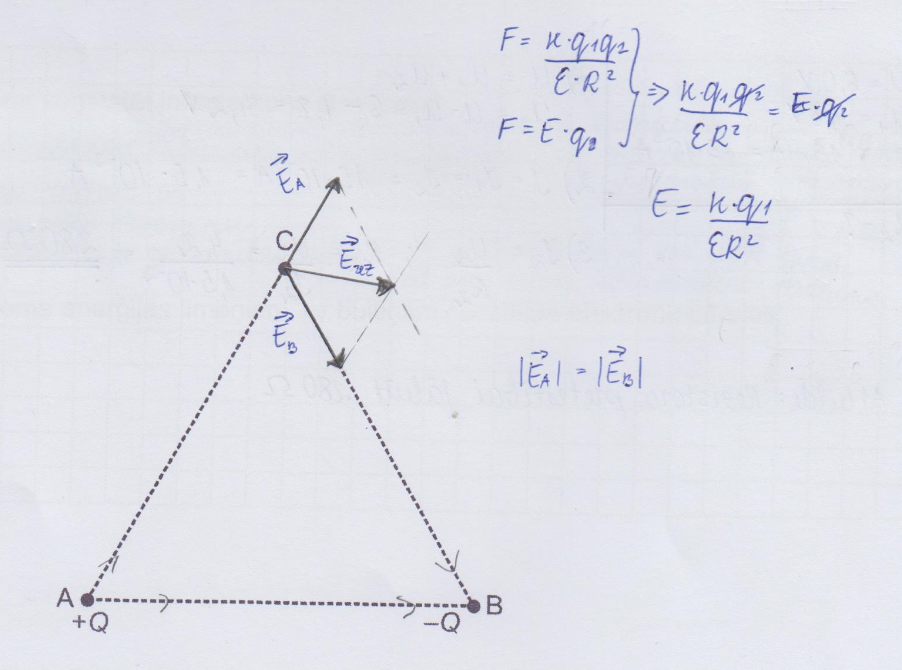
2. piemērs: risinājums novērtēts ar 0 punktiem.
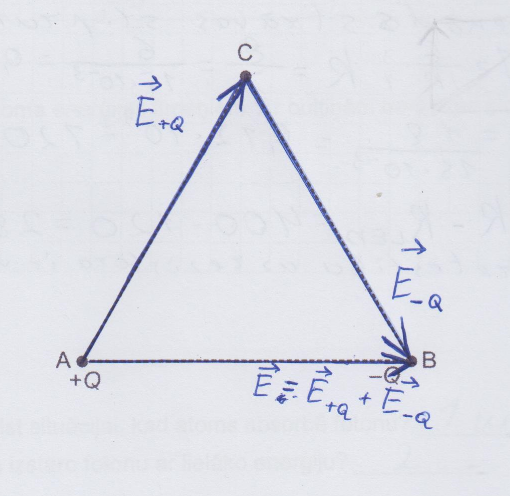
3. piemērs: risinājums novērtēts ar 0 punktiem.
4. piemērs: risinājums novērtēts ar 0 punktiem.