Attēlā redzams zvaigznes X emisijas līnijspektrs, kas iegūts, izmantojot difrakcijas režģa spektrometru.
Attēlā parādīti arī laboratorijā iegūti līnijspektri pieciem ķīmiskajiem elementiem.
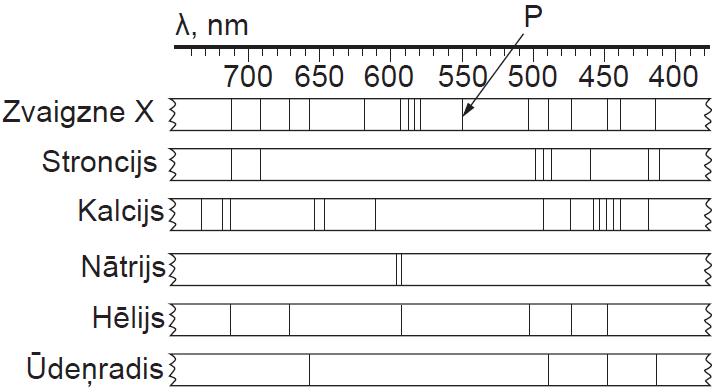
1. Kuri divi ķīmiskie elementi ir atrodami zvaigznes X atmosfērā? (1 punkts)
2. Difrakcijas režģim, ko izmantoja zvaigznes X spektra iegūšanai, bija 500 svītru milimetrā. Aprēķini, cik lielā leņķī novēro līnijai P atbilstošo pirmās kārtas difrakcijas maksimumu! (3 punkti)
3. Aprēķini spektra līnijas P viļņa garumam atbilstošā fotona kvanta enerģiju! (2 punkti)
4. Laboratorijā emisijas līnijspektrus ieguva, izmantojot līdz 5000 K temperatūrai sakarsētas vienatoma gāzes. Pamato, ka gāzes atoma vidējā kinētiskā enerģija šādā temperatūrā ir \(0,65~\mathrm{eV}\)! (2 punkti)
5. Skaidro, kā mainītos zvaigznes redzamais spektrs, zvaigznei attālinoties no novērotāja! (2 punkti)
1. Lai atbildētu uz šo jautājumu, jāzina, ka elektronam atomā nevar būt jebkuras vērtības potenciālā enerģija, bet tas var atrasties tikai noteiktos, diskrētos enerģijas līmeņos. Šos enerģijas līmeņus nosaka elektrona mijiedarbība ar kodolu un citiem elektroniem atomā.
Atomam pārejot no augstāka enerģijas līmeņa uz zemāku, tiek izstarota tieši tik liela enerģijas "porcija", kas vienāda ar enerģijas starpību starp šiem līmeņiem – EM starojuma kvants.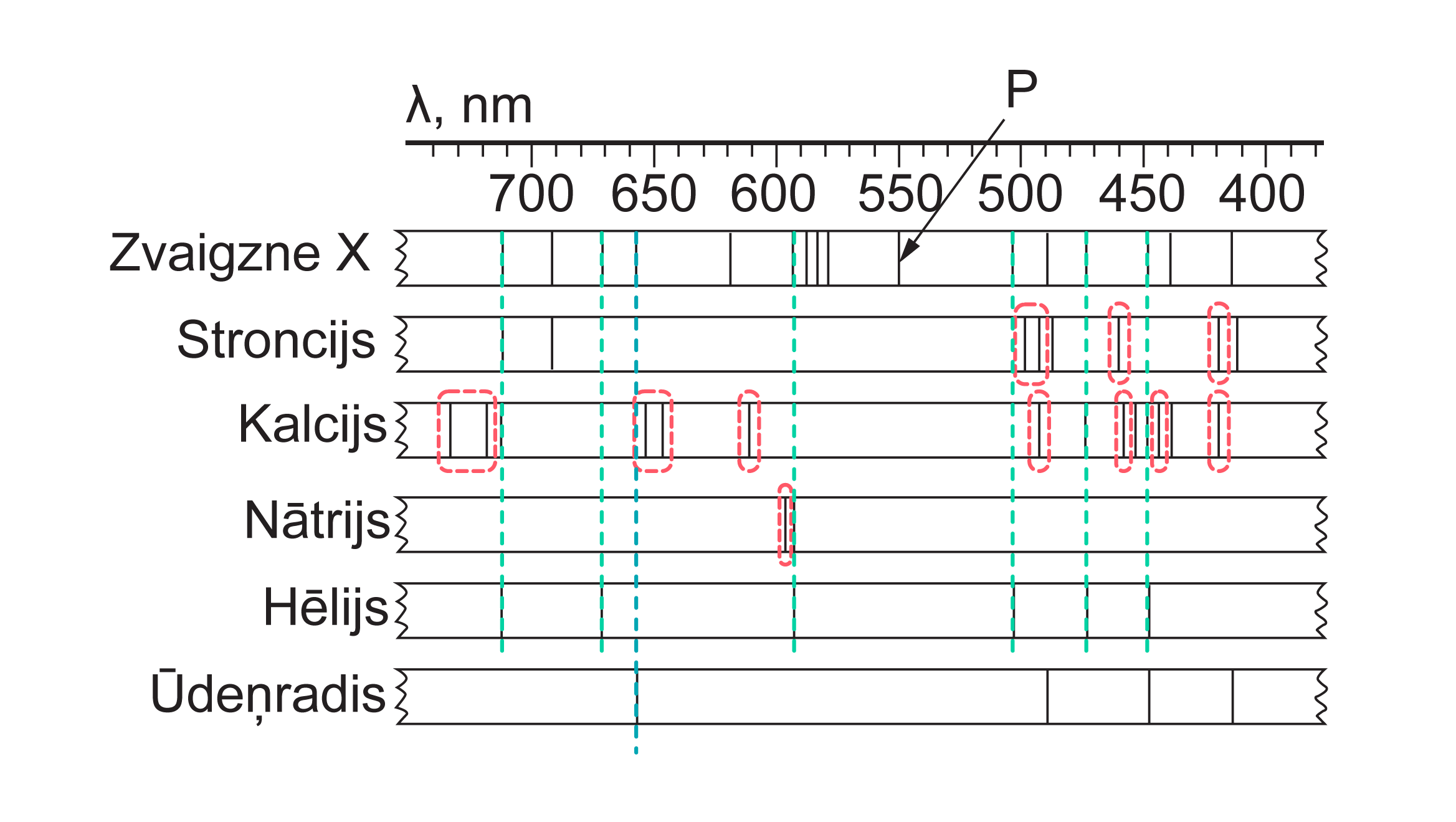
Eksperimentāli ir iespējams noskaidrot, tieši kādas enerģijas kvantus konkrētais ķīmiskais elements var izstarot – iegūt emisijas līnijspektru. Dažas līnijas dažādu elementu emisijas spektros var sakrist, bet to spektri noteikti nebūs pilnīgi vienādi.
Ja nezināmā vielā ir vairāki ķīmiskie elementi, tad tās spektrā jābūt visām vielā esošajiem elementiem atbilstošajām līnijām. Ja kāda ķīmiskā elementa spektrā ir kaut viena līnija, kādas nav nezināmās vielas spektrā, šāda elementa tajā nav.
Izpētot uzdevumā dotos spektrus var secināt, ka nezināmajā vielā ir He un H, bet pārējo elementu, kuru spektri parādīti, tajā noteikti nav.
Par atomu spektroskopiju vairāk var palasīt "Fiztēmās"’: https://www.fizmix.lv/fiztemas/atoms-un-atoma-kodols-10/energijas-emisija-un-absorbcija
Atbilde: ūdeņradis un hēlijs.
2. Jāatceras vai jāatrod datu bukletā difrakcijas režģa formula: \(k\lambda=d\sin\varphi\).
Spektra līnijai P atbilst viļņa garums \(\lambda\approx550\space\mathrm{nm}\) (pieņem \(\lambda\) vērtības robežās no \(545\space\mathrm{nm}\) līdz \(555\space\mathrm{nm}\)).
Jautāts par pirmās kārtas maksimumu, tātad \(k=1\).
\(d=\frac{1\space\mathrm{mm}}{N}=\frac{1\cdot10^{-3}\space\mathrm{m}}{500}=0,002\cdot10^{-3}\space\mathrm{m}=2\cdot10^{-6}\space\mathrm{m}\).
Izsakot leņķi \(\varphi\) no difrakcijas režģa formulas un ievietojot atbilstosās vērtības, iegūst: \(\varphi=\mathrm{arcsin}(\frac{k\lambda}{d})=\mathrm{arcsin}(\frac{1\cdot550\cdot10^{-9}}{2\cdot10^{-6}})\approx16^\mathrm{o}\).
Atbilde: līnijai P atbilstošo pirmās kārtas difrakcijas maksimumu novēro \(16^\mathrm{o}\) leņķī.
3. Kvanta enerģiju var aprēķināt, izmantojot datu bukletā atrodamo sakarību \(E=hf\) un sakarību, kas saista viļņa garumu, tā izplatīšanās ātrumu un starojuma frekvenci: \(f=\frac{c}{\lambda}\). Apvienojot izteiksmes iegūst: \(E=\frac{hc}{\lambda}=\frac{6,63\cdot10^{-34}\cdot3\cdot10^8}{550\cdot10^{-9}}\approx3,6\cdot10^{-19}\space\mathrm{J}=2,25\space\mathrm{eV}\).
Atbilde: spektra līnijas P viļņa garumam atbilstošā fotona kvanta enerģija \(E=3,6\cdot10^{-19}\space\mathrm{J}=2,25\space\mathrm{eV}\).
4. Jāzina vai jāatrod formulu lapā sakarība vienatoma gāzes vidējās kinētiskās enerģijas aprēķināšanai:
\(\overline{E_\mathrm{k}}=\frac{3}{2}kT=1,5\cdot1,38\cdot10^{-23}\cdot5000=1,04\cdot10^{-19}\space\mathrm{J}\).
Jāpārveido iegūto skaitlisko vērtību elektronvoltos:
\(1\space\mathrm{eV}=1,6\cdot10^{-19}\space\mathrm{J}\space\implies\space\frac{1,04\cdot10^{-19}}{1,6\cdot10^{-19}}\approx0,65\space\mathrm{eV}\).
5. Lai atbildētu uz jautājumu jāzina, ka par zvaigžņu attālināšanās ātrumu un kustības virzienu var spriest pēc to spektra līniju "sarkanās nobīdes" vai "zilās nobīdes".
Doplera efekta dēļ, gaismas avotam kustoties projām no novērotāja vai virzienā uz novērotāju, mainās novērotāja uztvertās gaismas viļņa garums \(\lambda\).
Doplera efekts ir novērotājam pienākošo svārstību frekvences (tātad, arī viļņa garuma) maiņa, ko rada svārstību avota un novērotāja pārvietošanās vienam attiecībā pret otru. Tas novērojams visu veidu viļņiem.
Doplera efekta cēlonis ir tas, ka, piemēram, viļņu avotam virzoties uz novērotāju, katra nākamā viļņa virsotne tiek izstarota no vietas, kas ir tuvāk novērotājam nekā iepriekšējā viļņa virsotne. Tātad tam vajag nedaudz mazāk laika, lai sasniegtu novērotāju, nekā iepriekšējam vilnim. Līdz ar to laika intervāls starp viļņu virsotņu pienākšanu novērotājam samazinās – notiek frekvences palielināšanās.
Doplera efektu ietekmē avota kustība, novērotāja kustība, vides kustības (skaņas viļņu gadījumā) vai jebkuras to kombinācijas. Elektromagnētiskajiem viļņiem, kas izplatās vakuumā, jāņem vērā tikai ātruma atšķirība starp novērotāju un avotu.
Analizējot tādu zvaigžņu spektrus, kuras attālinās, var konstatēt tā saukto sarkano nobīdi – spektrāllīnijas zvaigžņu spektros ir nobīdītas uz spektra "sarkano" galu.
Sarkano nobīdi \(z\) aprēķina kā spektrāllīnijas nobīdi \(\Delta\lambda\) attiecību pret spektrāllīnijas viļņa garumu laboratorijā \(\lambda\): \(z=\frac{\Delta\lambda}{\lambda}\).
Tātad, uzdevumā aprakstītajā situācijā zvaigznes spektrs "nobīdās" nedaudz pa kreisi, uz garāku viļņu pusi.
Kā Doplera efekta dēļ mainītos aborbcijas spektrs, vari ieskatīties "Vikipēdijā": https://lv.wikipedia.org/wiki/Sarkan%C4%81_nob%C4%ABde
Šeit var palasīt mazliet vairāk: https://itu.physics.uiowa.edu/labs/advanced/astronomical-redshift.
1. Vērtēšanas kritēriji
Nosaka abus ķīmiskos elementus: ūdeņradi un hēliju – 1 punkts. Skaidrojums nav nepieciešams.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
2. piemērs: risinājums novērtēts ar 1 punktu.
3. piemērs: risinājums novērtēts ar 0 punktu.
2. Vērtēšanas kritēriji
• Izmanto aprēķinā difrakcijas režģa formulu – 1 punkts.
• Nolasa līnijai P atbilstošo viļņa garumu un saista svītru skaitu milimetrā ar režģa konstanti – 1 punkts.
• Aprēķina leņķi, norāda mērvienību – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
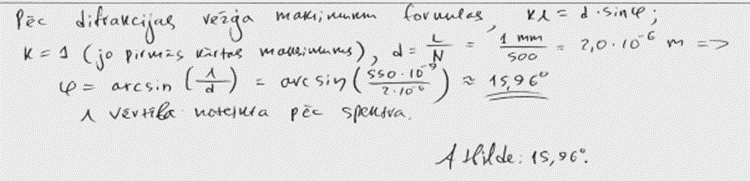
2. piemērs: risinājums novērtēts ar 3 punktiem.
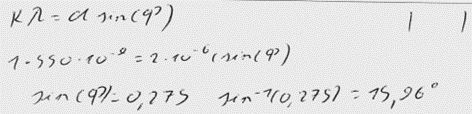
3. piemērs: risinājums novērtēts ar 2 punktiem. Kļūdas aprēķinā.
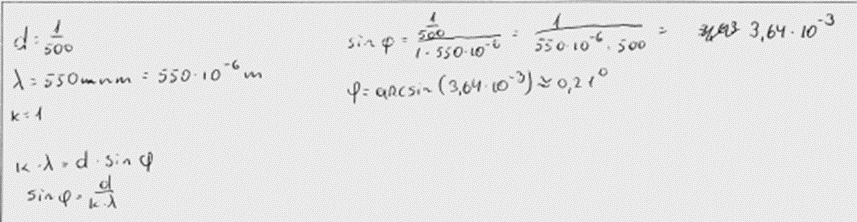
4. piemērs: risinājums novērtēts ar 1 punktu. Izpildīts tikai vērtēšanas kritēriju 1. punkts.
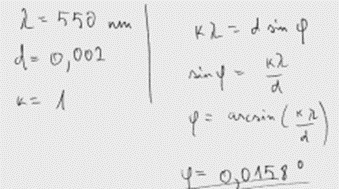
5. piemērs: risinājums novērtēts ar 0 punktu.
3. Vērtēšanas kritēriji
• Zina vai atrod datu bukletā un izmanto atbilstošās sakarības (\(E=hf\); \(f=c/\lambda\)) – 1 punkts.
• Aprēķina skaitliski, norāda mērvienību (J vai eV) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
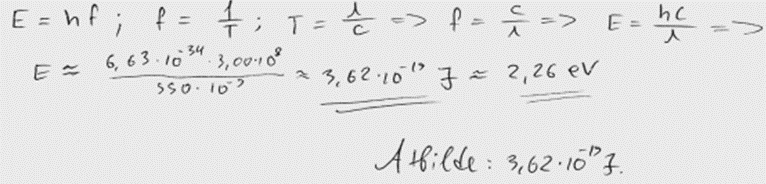
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 1 punktu. Izpildīts tikai vērtēšanas kritēriju 1. punkts.
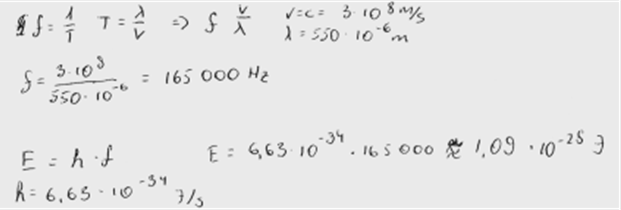
4. piemērs: risinājums novērtēts ar 1 punktu. Izpildīts tikai vērtēšanas kritēriju 2. punkts.
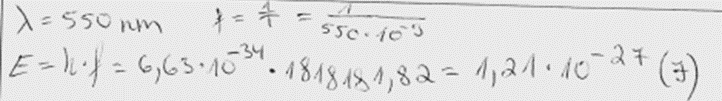
4. Vērtēšanas kritēriji
• Zina vai atrod datu bukletā un izmanto sakarību vienatoma gāzes molekulas vidējās kinētiskās enerģijas aprēķināšanai – 1 punkts.
• Salīdzina lielumu skaitliskās vērtības – 1 punkts.
Ja skolēns izvēlējies risinājuma veidu, kas nav aprakstīts kritērijos, vērtētājs patstāvīgi sadala risinājumu soļos, atbilstoši dotajam punktu skaitam.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
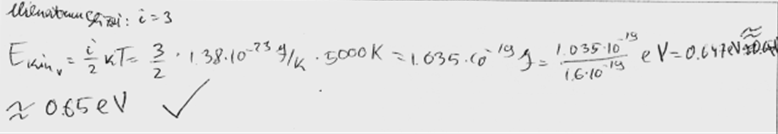
2. piemērs: risinājums novērtēts ar 2 punktiem.
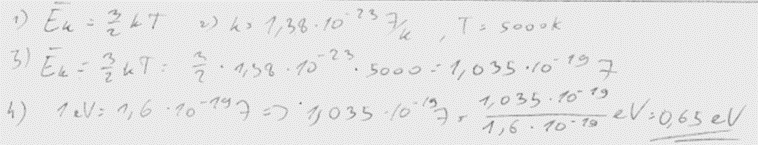
3. piemērs: risinājums novērtēts ar 1 punktu. Izpildīts tikai vērtēšanas kritēriju 2. punkts.
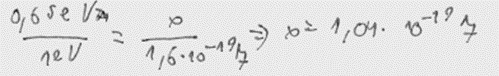
5. Vērtēšanas kritēriji
• Atsaucas uz Doplera efektu un/vai "sarkano nobīdi" – 1 punkts.
• Secina, ka spektra līniju viļņu garums palielināsies, spektrs nobīdīsies uz garāku viļņu pusi – 1 punkts.
Pamatojums var būt neprecīzs.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 2 punktiem. Gaismas ātrums nav atkarīgs no atskaites sistēmas, tādēļ šo formulu izmantot nav korekti. Punktu ieskaita.
4. piemērs: risinājums novērtēts ar 1 punktu. Risinājums nepilnīgs un pieraksts nekorekts. Pēdējais teikums pretrunā ar iepriekšējo. Iespējams – neuzmanības kļūda.
5. piemērs: risinājums novērtēts ar 0 punktu.
6. piemērs: risinājums novērtēts ar 0 punktu.
7. piemērs: risinājums novērtēts ar 0 punktu.
